
掲載画像:複素平面(ガウス平面)に描かれたマンデルブロート集合の図形
「複素世界は実世界とつながっている」という記事で中学、高校で習う数学公式の多くが複素数の世界でも成り立っているのが不思議だと説明した。そして「それを成り立たせる「理由」がどこかにあるはずだ。」とまで書いたのだが、今日の記事ではその理由を示そう。
それは「実数で成り立つ演算規則は複素数でもそのまま成り立つから。」という一言に尽きる。つまり実数で成り立つ加減乗除(+-×÷)、交換法則、分配法則、結合法則、指数法則などはすべて複素数でも同じ形で成り立っているからだ。(幾何学的、物理的に意味を持つかは別としてだが。)
交換法則:
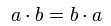
分配法則:
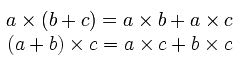
結合法則:
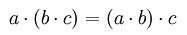
指数法則:
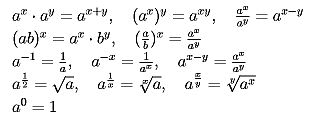
2次方程式の解の公式にせよ、三角関数の加法定理にせよ、微分の公式にせよ、最終的にはこのような基本的な演算規則によって実数の場合には証明されている。ということはその証明はそのまま複素数についても成り立っているわけだ。
2次方程式の解の公式の証明は上記の演算規則の組み合わせであることは明らかだろう。
微分の公式については「微分の定義式」に戻って考えてみれば明らかだ。
三角関数の加法定理については若干の説明が必要かもしれない。高校ではこのページの説明のように幾何学的な方法を使って証明していた。複素数についてはこの方法は使えない。
複素数の場合は次のような方法をとる。まず、実数変数α、βについてオイラーの公式から以下のように加法定理が証明されることを思い起こす。

そして、sin α、sin β、sin(α+β)、cos α、cos β、cos(α+β)はそれぞれ次の式の右辺の形に書き表せることを思い起こす。
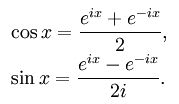
ここでαとβ、x(エックス)は実数であるが、同じ公式でそのまま複素数α、β、x(エックス)でも成り立つことは明らかだ。(「角度」に相当する変数が複素数になっても成り立つということ。)
そしてこの右辺の形の式を上記の「加法定理の導出」に掲載した式に代入すると、sinとcosを使わない形に書き表すことができ、加法定理が成り立っていることが証明される。
複素数が中学、高校で習う数学公式でも成り立っていることは不思議に見えたが、その元をただせば、上記の基本的な演算規則が成り立っているからなのだ。教科書でこれらは「数」について学習するときまず登場するわけだが、当たり前すぎて軽視してしまうことが多いことだろう。
けれども基本的な演算規則がさまざまな法則の源となっていることを知ると、その重要さにあらためて気がつかされるのだ。シンプルさゆえに応用範囲は計り知れない。
ところで複素数を拡張した「四元数(Quaternion = クォータニオン)」についてはどうだろうか?
四元数とは虚数単位をi, j, kとするときこのような形で書き表せる。
q = s + iu + jv + kw (ただしs, u, v, wは実数)
残念ながら四元数では交換法則は成立しないので、実数や複素数で成り立つ基本演算は少し違ったものになる。だから中学や高校で習う公式は一般的には成り立たない。
けれどもそれは残念なことではなく既に導かれた公式に四元数をあてはめるとまた別の数学公式の体系(=法則)が生まれるかもしれない可能性を秘めている。
- 四元数を係数にもつ2次方程式と解の公式は?
- 四元数を変数とする三角関数や指数関数は定義できるだろうか?
- 四元数の世界で微分や積分はどうなっているだろうか?
- 四元数世界に拡張されたオイラーの公式は見つかるだろうか?
それらは意味のあることかもしれないし、意味がないかもしれない。
どうなるのか僕にもわからないが「新たな発見」に挑戦してみてはいかがだろうか。
オイラーの公式の四元数への拡張式は次のように表せそうです。導き方はこの記事のコメント欄を参照。
=================================
e^(iθ+jφ+kψ)
=cos{√(θ^2+φ^2+ψ^2)}
+{(iθ+jφ+kψ)/√(θ^2+φ^2+ψ^2)}
・sin{√(θ^2+φ^2+ψ^2)}
=================================
なお、ネット上にも見つけることができた。
オイラーの公式の四元数への拡張
http://math.stackexchange.com/questions/41574/can-eulers-identity-be-extended-to-quaternions
https://www.quora.com/Is-there-a-quaternion-counterpart-to-eulers-formula
オイラーの公式の四元数への拡張を動画で解説
応援クリックをお願いします!

関連記事:
複素世界は実世界とつながっている
http://blog.goo.ne.jp/ktonegaw/e/b060d7aed8c03454f25fdf81ca69c446
虚数は私たちの世界観を変えてしまった。
http://blog.goo.ne.jp/ktonegaw/e/ed35400df27a2bc7e597531c08d99869
虚数や複素数に大小がないのはなぜ?
http://blog.goo.ne.jp/ktonegaw/e/398b0d7e84eb491dea9c38a15e994256
複素数 a+bi のプラス記号は「足す」という意味?
http://blog.goo.ne.jp/ktonegaw/e/e29c7f0e787464693ff26ab287b34ddd
博士の愛した数式とGoogleの電卓機能
http://blog.goo.ne.jp/ktonegaw/e/0d7855769ea29ddd42d0ddad25f13046
虚数の情緒
http://blog.goo.ne.jp/ktonegaw/e/27155c8d7b5242d7e69e00335411acc1
ヴィジュアル複素解析
http://blog.goo.ne.jp/ktonegaw/e/2f47e7b748d4ca7022dc53305388a00b
因数分解って何の役に立つの?
http://blog.goo.ne.jp/ktonegaw/e/e54dfcd47b72ae247a22206c05bfaa8e
























※以下、iを虚数単位とします。a^bは、aのb乗のこととします。
オイラーの公式
e^(iθ)=cosθ+isinθ
がマクローリン展開式から導かれたことは有名ですが、
これを四元数に応用したらどうなるだろうかと考えてみました。
1)オイラーの考察の復習
e^x=x^0/(0!)+x^1/(1!)+x^2/(2!)+x^3/(3!)+x^4/(4!)+x^5/(5!)+..
…[1]
このxにiθをあてはめて、
e^(iθ)=(iθ)^0/(0!)+(iθ)^1/(1!)+(iθ)^2/(2!)+(iθ)^3/(3!)
+(iθ)^4/(4!)+(iθ)^5/(5!)+...
=1+iθ/(1!)-θ^2/(2!)-iθ^3/(3!)+θ^4/(4!)+iθ^5/(5!)-θ^6/(6!)...
={1-θ^2/(2!)+θ^4/(4!)-θ^6/(6!)...}
+i{θ/(1!)-θ^3/(3!)+θ^5/(5!)-...}
=cosθ+isinθ
2)四元数に応用
※今度は考える場を拡張して、i,j,kを四元数における3つの
「虚数単位」とします。
[1]式を、e^(iθ+jφ+kψ)について考察します
(θ,φ,ψは実数とします)。
ただし、次のことに注目します。
また、四元数では可換律が成り立たないことに注意します。
θ^2+φ^2+ψ^2>0としておきます。
(iθ+jφ+kψ)^0=1
(iθ+jφ+kψ)^1=iθ+jφ+kψ
(iθ+jφ+kψ)^2=-(θ^2+φ^2+ψ^2)
(iθ+jφ+kψ)^3=-(θ^2+φ^2+ψ^2)(iθ+jφ+kψ)
(iθ+jφ+kψ)^4=(θ^2+φ^2+ψ^2)^2
(iθ+jφ+kψ)^5={(θ^2+φ^2+ψ^2)^2}(iθ+jφ+kψ)
(iθ+jφ+kψ)^6=-(θ^2+φ^2+ψ^2)^3
(iθ+jφ+kψ)^7=-{(θ^2+φ^2+ψ^2)^3}(iθ+jφ+kψ)
(iθ+jφ+kψ)^8=(θ^2+φ^2+ψ^2)^4
...
すると、[1]の展開式は、e^(iθ+jφ+kψ)では、
e^(iθ+jφ+kψ)
=(iθ+jφ+kψ)^0/(0!)+(iθ+jφ+kψ)^1/(1!)
+(iθ+jφ+kψ)^2/(2!)+(iθ+jφ+kψ)^3/(3!)
+(iθ+jφ+kψ)^4/(4!)+(iθ+jφ+kψ)^5/(5!)+...
+(iθ+jφ+kψ)^6/(6!)+(iθ+jφ+kψ)^7/(7!)+...
=1+(iθ+jφ+kψ)/(1!)
-(θ^2+φ^2+ψ^2) /(2!)- (θ^2+φ^2+ψ^2) (iθ+jφ+kψ)/(3!)
+(θ^2+φ^2+ψ^2)^2/(4!)+{(θ^2+φ^2+ψ^2)^2}(iθ+jφ+kψ)/(5!)
-(θ^2+φ^2+ψ^2)^3/(6!)-{(θ^2+φ^2+ψ^2)^3}(iθ+jφ+kψ)/(7!)
={1-(θ^2+φ^2+ψ^2)/(2!)+(θ^2+φ^2+ψ^2)/(4!)
-(θ^2+φ^2+ψ^2)/(6!)...}
+(iθ+jφ+kψ){1/(1!)-(θ^2+φ^2+ψ^2)/(3!)+(θ^2+φ^2+ψ^2)^2/(5!)
-...}
={1-A^2/(2!)+A^4/(4!)-A^6/(6!)...}
+(iθ+jφ+kψ)/A・{A/(1!)-A^3/(3!)+A^5/(5!)-...}
=cosA+(iθ+jφ+kψ)/A・sinA
(※但し、A=√(θ^2+φ^2+ψ^2)とおいた)
よって、オイラーの公式の四元数(虚数)への拡張式は
次のように表せそうです。
================================================================
e^(iθ+jφ+kψ)
=cos{√(θ^2+φ^2+ψ^2)}
+{(iθ+jφ+kψ)/√(θ^2+φ^2+ψ^2)}
・sin{√(θ^2+φ^2+ψ^2)}
================================================================
こんな感じでしょうか?
すごいです!手放しで喜んでしまいました!(笑)
僕は記事の中で「四元数世界に拡張されたオイラーの公式は見つかるだろうか?」と何気なく書いただけなのに、実際はこんなふうになるわけですね!
自分でも検算してみましたが、確かにこうなりますね。うーむ、すばらしい。。。
ブログの他の読者の方も、このようなコメントを目にして、ますます数学の世界の奥深さを感じていただけるのではないでしょうか。
ありがとうございます!
もう1回お邪魔させていただきます。
オイラーの公式の四元数への拡張式は
次のように表せる。として、
==========================================
e^(iθ+jφ+kψ)
=cos{√(θ^2+φ^2+ψ^2)}
+(iθ+jφ+kψ)/√(θ^2+φ^2+ψ^2)
・sin{√(θ^2+φ^2+ψ^2)}
=========================================
上式で、θ=φ=ψ=π/√3とおけば、
e^{(i+j+k)π/√3}
=cosπ+(i+j+k)(π/√3)/π・sin(π)
=cosπ+(i+j+k)/√3・sin(π)
=cosπ=-1
よって、
=====================
e^{(i+j+k)π/√3}+1=0
=====================
が成立する(と思います)。
なかなか面白い式ではないでしょうか?
e,π,i,j,k,√3,1,0の関係式です。
それでは失礼します。...
またまた質の高いコメントをいただきありがとうございます!
これはまた美しい関係式を導きだしましたね。
当てずっぽうですけれども、八元数のときの関係式は次のようになるような気がしてきました。
=====================
e^{(i+j+k+l+m+n+o)π/√7}+1=0
=====================
訪問させて頂きました。
複素数の範囲のみならず、四元数の世界に拡張したら
どうなるだろう、と。
自分では思いついても、実際に定義と計算の仕方がわからなかったので、このブログの記事にたどり着き
素敵なやりとり感動しました。
思いつきが数学的に意味のある体系になるというのは
数学の醍醐味だと思います。
四元数はさまざなところで活躍しているようですね
四元数の世界での微分・積分も興味があります。。
また、係数を四元数としたときの二次関数の解と係数に同じく興味があります。
代数学の基本定理にあるように、
複素数を係数とする方程式は 解は複素数の範囲に
必ず治ることは 周知のことですから、
四元数の場合はどうなるんだろう、と思います。
コメントありがとうございます。
今はちょうどNHK数学ミステリー白熱教室が放送されている期間で、一般化された数学への興味が高まっていますね。4元数の代数はクリフォード代数として一般化されます。ウィキペディアで調べてみると「クリフォード代数は幾何学、理論物理学、デジタル画像処理を含む種々の分野において重要な応用を持つ。」と書かれていますし、興味が尽きない世界ですね。
ネット上に以下のページや動画を見つけたので本文記事に追記しておきました。
オイラーの公式の四元数への拡張
http://math.stackexchange.com/questions/41574/can-eulers-identity-be-extended-to-quaternions
https://www.quora.com/Is-there-a-quaternion-counterpart-to-eulers-formula
オイラーの公式の四元数への拡張を動画で解説
https://www.youtube.com/watch?v=88BA8aO3qXA
四元数では一般に割り算が出来ないので、
微積分学の構築はなかなか難しいみたいです。
が、やってる人はいるみたいです:
C. A. Deavours, "The Quaternion Calculus" The American Mathematical Monthly
Vol. 80, No. 9 (Nov., 1973), pp. 995-1008
ただ、多様体論を展開しようとすると、
(実や複素と違って)四元数平面は良いモデル空間ではなく、
バンドルや接続などを用いて「四元数多様体」が定義されるみたいです。
四元数のオイラーの公式は、これはこれで良い気もしますが(項別微分や和の順序を入れ替えてるので、本当は級数の(絶対・一様)収束性など色々気にしないといけないのですが)、個人的には、「四元数冪とは何か」をちゃんと考えてみると、色々広がりもある気がします(マクローリン展開に代入する定義は妥当かなど・・・?)
数学の様々な概念をより広い世界に拡張するというのは面白いことですが、
それによって、今まで扱っていたものの関係が説明できると、もっと面白いですね。
例えば、複素数の指数関数の場合は、
複素数まで拡張することにより、指数関数と三角関数が統一的に扱えるということがわかったわけです。
また、複素積分などは、実の広義積分の計算などにも応用されます。
概念や公式を広い世界に拡張したあとは、
そのような応用を見つけることも、大切なこと(むしろ、そこに数学の「面白さ」がある)だと思います。
ありがとうございます。四元数の多様体のことなど考えてもみませんでした。その定義自体が面倒なものなのですね。
掛け算ができて(一般的には)割り算ができないというのも不思議な世界ですね。
四元数の初等関数については、次のPDF資料を見つけました。
四元数とその初等関数・逆関数を扱うための準備
http://www.aihara.co.jp/~taiji/tp/upload/1292868622-q-fundamental.pdf
y = √(b^2+c^2+d^2), I = (b i + c j + d k)/y として
z = x + y I と書くと、z だけを使う計算は普通の複素数 z = x + y i の計算と全く同じになるんですよねー。
オイラーの公式も z だけですから当然同じになります。
逆に実二次方程式の複素解は上の I が全部解なので無限個あることになります。