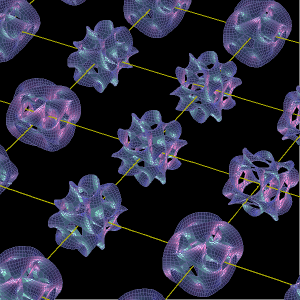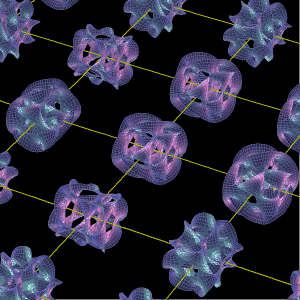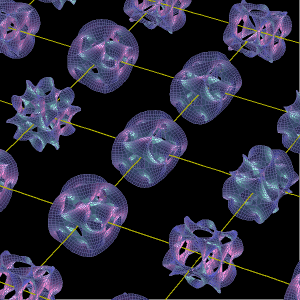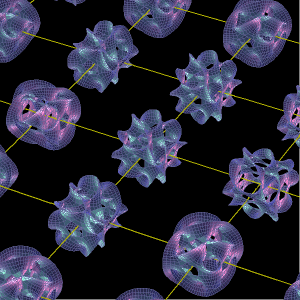
超ひも理論やM理論によればこの世界は10次元空間に存在する振動する「超ひも」や11次元空間に存在する「膜」からできているそうだ。原子や電子を構成するさまざまな素粒子はこの弦が多様に振動する結果にすぎない。
超ひもが存在する10次元のうち6つの(余分な)次元はドーナツ型に丸まってしまって、時間と空間の1次元+3次元=4次元に住む私たちには見えない。この6次元のドーナツのことを発見した数学者の名にちなんで「カラビ-ヤウ空間(カラビ-ヤウ多様体)」という。(数学的にはカラビ-ヤウ多様体はn次元だが、超弦理論ではそのうち6次元のものが研究対象になる。)掲載画像は私たちにも見えるように3次元空間に投影したものだ。それぞれのカラビ-ヤウ多様体の大きさはは超ひもとほぼ同じで10のマイナス33乗センチメートルだ。水素原子のサイズが10のマイナス8乗センチメートル、電子のサイズが10のマイナス17センチメートルなので、これがいかに小さいかということがおわかりであろう。超ひも理論やM理論が相対性理論と量子力学を統一するこの世界の究極理論だとすると、このドーナツ型をしたものが空間のあらゆる点に存在しているそうだ。超ひも理論で、巻き上げられているカラビ・ヤウ空間の性質に「特定の操作を加えると、できた新しい空間が持つ偶数次元の穴の数が、もとの空間の持つ奇数次元の穴と数が等しくなる」という。(ワケわからん!)
掲載画像はこのページから拝借した。Mathematicaを使って描いたようだ。もともとの画像は掲載画像よりも鮮明なので掲載元のアニメーションをご覧いただきたい。
先日紹介した「エレガントな宇宙」の紹介記事はこのページで読めるが、ここにもカラビ-ヤウ多様体の図が掲載されている。また、このページでは掲載画像とは別のカラビ-ヤウ多様体がQuickTimeアニメーションで見れる。
竹内薫先生の「超ひも理論とはなにか」の表紙に使われているのもカラビ-ヤウ多様体である。

カラビ-ヤウ多様体について検索するうちに、これを理解するためにはかなりの数学的知識と経験が必要なようだ。キーワードを「カラビ-ヤウ多様体」として検索すると次のようなページがヒットする。群論、多様体、微分幾何学などまだまだ数学を勉強してからでないと歯が立たないようだ。まだ登山口にも着いていない気がする。道のりは遠い。。。

微分幾何学の最先端:
http://www.baifukan.co.jp/sinkan/shokai/mokuji/003476t.html
超弦理論のコンパクト化に基づく標準模型へのアプローチ:
http://www.icepp.s.u-tokyo.ac.jp/tokutei/outcomes/c01jun2006.html
原理の探求:
http://www.phys.sci.osaka-u.ac.jp/coe/program/principles.html
超弦理論の現象論・宇宙論への応用:
http://www-gauge.scphys.kyoto-u.ac.jp/pages/activity-pics/intro3.html
おまけ:携帯電話の待受けアニメーション画像
上で紹介したカラビ-ヤウ空間の画像を使って待受け画像を作ってみた。(240x240ピクセル)ファイル・サイズに制限があったのでなめらかに回転する動画にはならなかったが、このURLを自分の携帯メールに転送して使ってください。

カラビ-ヤウ多様体のステレオグラム動画を見つけたので紹介しておこう。手ごろなサイズで表示させて見てほしい。(立体視をするための方法)
関連記事:
見えざる宇宙のかたち:シン=トゥン・ヤウ、スティーヴ・ネイディス
http://blog.goo.ne.jp/ktonegaw/e/943c5a3cf09a78c3b4e8e933ce379879
番組告知:NHKスペシャル「神の数式」(2013年 9月21日、22日)
http://blog.goo.ne.jp/ktonegaw/e/1a809c46b31c32b3b3c84dc0be881ddc
NHKスペシャル「神の数式」の感想
http://blog.goo.ne.jp/ktonegaw/e/a2368bbcee58771d16dbcb4613dc077d
解説:NHKスペシャル「神の数式」第1回:この世は何からできているのか
http://blog.goo.ne.jp/ktonegaw/e/5f0430e3fed08f6947d5efbe9559fbbd
解説:NHKスペシャル「神の数式」第2回:宇宙はどこから来たのか
http://blog.goo.ne.jp/ktonegaw/e/7ddecf5c37c9ef0e467bb5be8f168898
番組告知:NHK-BS1「神の数式 完全版」全4回 (2013年12月24日~27日)
http://blog.goo.ne.jp/ktonegaw/e/d763b4d8161efae445f37e05ab23f1e6
番組の感想:NHK-BS1「神の数式 完全版」
http://blog.goo.ne.jp/ktonegaw/e/d63e471fcfd568bb2c5646646792e3cb
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。




























私は小さい頃にニュートンが読める小児科に通っていたというだけで、いい大人になって再び興味を持ち始めつつある者です。いくつになっても、好奇心は忘れずにいきたいものですね。
はじめまして。コメントありがとうございます。
「ニュートンが読める小児科」というのはいいですね。
この記事を書いたのは2006年12月。待受画像は当時の携帯で許容されるGIFファイルの最大バイト数に合わせて作ったのですが、あれから携帯はずいぶん高性能化したものだとあらためて思いました。
ニュートンムック(ニュートン別冊)にも素晴らしい入門書が揃ってきました。常に新しい知識や考え方にワクワクしている人生を送りたいものです。
コメントいただき、ありがとうございます。気がつくのが遅くなり、失礼いたしました。
そうですね。現在の理論は現在を基準に打ち立てられているから、きわめて長い時間に動的に変化している宇宙を1次近似で見ているだけかもしれません。大統一理論では宇宙開始のごく初期の段階で4つの力が統一されていましたが、長い時間のスケールでは万有引力定数Gをはじめ、さまざまな宇宙定数が変化している可能性も考えられます。
ご指摘ありがとうございます。10年も前の記事で、当時は勉強不足でした。
正しくは「超弦理論で考えるカラビ-ヤウ空間は6次元」です。数学的にはカラビ-ヤウ多様体はn次元のものが考えられるわけですが、超弦理論では6次元の余剰次元空間が研究対象になります。
記事の本文を修正しておきました。
ちなみにM理論(時空次元が11次元)のときにどうなるのか、僕はまだ理解できていません。
それから時間が5次元だといわれましたがよく理解できません。外国の研究者の訳本を読んだら相対性理論で数学的には時間は4番目の次元なっているから時間は4次元であると書いてあります。また他の書物で時間軸を含めた4次元空間と書いてありますので時間は4次元ということになります。今まで私はそういうことで時間は4次元とばかり思っていました。
M理論のときのカラビ-ヤウ空間について、今後わかったらコメント欄を通じてお伝えしますね。
時間の次元についてですが、鈴木さまの勘違いの原因がようやくわかりました。つまりこういうことです。
ニュートン:1番目から3番目の次元は空間、4番目の次元は時間です。つまり空間は3次元、時間は1次元です。数学っぽく座標で書くと次のようになります。
空間:(x1, x2, x3)
時間:(t)
アインシュタイン:空間は3次元、時間は1次元なのですが、空間と時間が一体となった「時空」を考えるので「時空としての次元」は3+1=4次元です。数学っぽく座標で書くと次のようになります。
時空:(x1, x2, x3, t)
カルツァ・クライン理論、リサ・ランドール博士の理論(そして鈴木さまのお考え)では「空間」だけで4次元と考えていますね。
カルツァ・クライン理論
http://goo.gl/NVI80C
リサ・ランドール博士の理論
http://kamakura.ryoma.co.jp/aoki/paradigm/Lisa.htm
そして「時間」の次元は相変わらず過去から未来へ伸びる「1次元」です。空間だけで1番目から4番目の次元をあらわしているから、時間の次元は5番目の次元となるわけです。そうすると4+1=5次元になります。そしてアインシュタインのように空間と時間は一体ですから4次元空間の宇宙論での「時空」の次元は5になるのです。数学っぽく座標で書くと次のようになります。
時空:(x1, x2, x3, x4, t)
このうち4番目の空間次元の x4 は、これまでのやり取りからわかるようにコンパクト化されていることになりますね。
超弦理論では空間を9次元、時間を1次元と考え、時空としての次元数は10です。数学っぽく座標で書くとこのようになります。
超弦理論の時空:(x1, x2, x3, x4, x5, x6, x7, x8, x9, t)
このうち6次元の(x4, x5, x6, x7, x8, x9)の空間がコンパクト化されているカラビ-ヤウ空間をあらわしているのだろうと考えられているわけです。
> 相対性理論で数学的には時間は4番目の次元なっているから時間は4次元であると書いてあります。
これは間違いですね。時間はどの理論であっても今のところは1次元です。(2次元以上の時間次元を考える理論もありますが、ごく少数派です。)
> また他の書物で時間軸を含めた4次元空間と書いてありますので時間は4次元ということになります。
正しくは「時間は4番目の次元」で「時空は4次元」ということになります。
いいえ、時間の次元は空間の次元と関係ありません。ニュートンの理論、アインシュタインの理論、カルツァ=クラインの理論、超弦理論、M理論のどれであっても「時間の次元数は1」です。
アインシュタインの4次元の時空: (x1, x2, x3, t)
ですが、時間が2次元、3次元、4次元だとすると
時間が2次元の5次元時空:(x1, x2, x3, t1, t2)
時間が3次元の6次元時空:(x1, x2, x3, t1, t2, t3)
時間が4次元の7次元時空:(x1, x2, x3, t1, t1, t2, t3, t4)
のようになってしまいます。このような理論を考える物理学者はほとんどいません。
> 高次元空間になるほど時間の次元が上がって行くようですね。
いいえ、違います。鈴木さまが「上がっていく」とおっしゃっているのは時間のtの位置が( , , , )の座標の取り方で右にずれていくからそうお考えになったのだと思いますが、( , , , )の中の位置と次元数は関係ありません。
また、「○次元」、「次元数」、「○番目の次元」という言葉を混同されているようにも思えます。
私の返信を正しく読み取られていませんね。
> 貴方は前カルツア・クラインの理論を引用して時間は5次元であると言われたのと同じ意味です。
いえ、私はそのようなことは言って(書いて)いませんよ。私が書いたのは「(カルツア・クラインの理論のように)4次元空間の宇宙論での「時空」の次元は5になるのです。」
「時間」と「時空」の意味は違います。鈴木様はこの2つを混同しているように思います。
申し訳ありませんが、これ以上のコメントは控えていただきますようお願いします。
> あなたは以前に「カルツア=クライン理論で提唱された5次元時空(4次元空間+1次元の時間)と同じモデルと書いておられますよ。
はい、そのとおりです。
> だから5次元時空ではその中の一つの次元が時間になっていて5次元が時間になっていることと同じではないですか。
いいえ、違います。
鈴木さまは「5次元」、「第5次元」、「5番目の次元」という3つの言葉の使い分けができていないから、そのように誤解なさっているわけです。
正しくは
「5次元時空ではその中の一つの次元が時間になっていて第5次元が時間になっている」
あるいは
「5次元時空ではその中の一つの次元が時間になっていて5番目の次元が時間になっている」
となります。以下のように言葉を使い分けます。
5次元とは全体の次元数を合計した数
第5次元=5番目の次元
リンゴを5個並べたときのことを考えてみましょう。
全体の個数は5個です。
このときリンゴ全部の個数は5個です。
リンゴを左から順番に数えていって右端のリンゴは「5番目の」リンゴといいますね。
右端のリンゴだけを指しているときに「リンゴの個数は5個です」とは言いませんよね。
鈴木さまの言葉遣いの間違いはこれと同じです。
それからM理論は名前だけ知っていると申しましたが、内容も少しだけわかりました。しかし超弦理論がまだ不完全な理論であることは残念ですね。超弦理論はEOTといわれているので。
ご理解いただき、ありがとうございます。
誤解の原因は言葉の表現によるもので、鈴木さまが正しく理解されていたことがわかりました。
超弦理論には5種類の異なった理論があり、そのどれもが成り立っているという問題がありました。でも、それはひとつの大きな理論がとっている別々の形であることをウィッテン博士が発見し、M理論と名付けたわけですね。だからM理論には5種類の超弦理論が含まれています。
Mはmembrane(膜)やmother(母)、magic(魔法)、mystery(謎)などの頭文字といわれていますが、M理論の名付け親のウィッテン博士もどれがその意味であるかを明らかにしていません。(わざとそうしているのでしょう。)
2次元空間のカラビ-ヤウ図形について考えてみましたが、判りませんでした。2つの直交する円だとしましたがこれは正しくないようです。3次元空間のカラビ-ヤウ図形はさらに難しいと思います。
超弦理論は完成にカラビ-ヤウ図形が障害
になっているのですか。
どういたしまして。
「図形」というものは次元の数が増すにつれて、複雑になり難しくなっていきますね。
カラビ-ヤウ空間を学ぶためにはトポロジーや多様体、微分幾何学など大学3年以降で学ぶ数学が必要になります。ウィキペディアで調べると、とてもたくさんの数学を学ばないと理解できないことがわかると思います。僕も理解できていません。
カラビ-ヤウ多様体(カラビ-ヤウ空間):ウィキペディアの記事
http://goo.gl/lF73Xu
ただし、一般向けにカラビ-ヤウ空間のことを解説した本が1冊だけあります。
見えざる宇宙のかたち:シン=トゥン・ヤウ、スティーヴ・ネイディス
http://blog.goo.ne.jp/ktonegaw/e/943c5a3cf09a78c3b4e8e933ce379879
> 超弦理論は完成にカラビ-ヤウ図形が障害になっているのですか。
3つの障害(問題)が知られています。
1) カラビ-ヤウ空間の中の2つの位置の間に「距離」が定義できないこと。
2) ラグランジアンが定義できないこと。
ラグランジアンは物理ではとてもよく使われる基本的な量で、「解析力学」の中で学びます。超弦理論ではこのように基本的な量が定義できないのです。
ラグランジアンの物理的な意味
http://dreistein.hatenablog.com/entry/2015/01/15/080000
3) 3次元空間の「形」に球やドーナツ、そして穴が2つ空いた形....などいろいろな種類があるように、6次元のカラビ-ヤウ空間にもさまざまな種類があります。その個数は10の500乗もあると言われています。どれを採用するかによって、できあがる宇宙の物理法則が異なってきます。自由度がありすぎるわけですね。そのうちのどれが私たちの住んでいる宇宙なのかがわかっていません。
この3つの障害(問題)について一般向けに書かれた本としては、やはり大栗博司先生の本がお勧めですね。
大栗先生の超弦理論入門:大栗博司
http://blog.goo.ne.jp/ktonegaw/e/75dfba6307d01a5d522d174ea3e13863
さらに詳しくお知りたいようでしたら、次の本がよいでしょう。
エレガントな宇宙:ブライアン・グリーン
http://blog.goo.ne.jp/ktonegaw/e/404c24b68f57609900bc3d7a030333d5
私も考えて成功したと思ったら失敗でした。もう一度考えてみ
ます。貴方が言われました原子レベルのテレーポテーションについてご説明いただくと幸いです。
数学の空間としてのカラビ-ヤウ図形はn次元で考えるようですが、1次元空間や2次元空間のカラビ-ヤウ図形はないと思いますよ。だから考えても意味がありません。
そして通常、数学で扱うカラビ-ヤウ図形(多様体)は複素数の次元で考えます。複素1次元は実数軸と虚数軸の2本があるから実次元では2次元となります。複素2次元は実次元では4次元となります。
カラビ-ヤウ図形は大学や大学院のレベルの数学(トポロジーや複素多様体)の勉強を終えてからでないと、考えても意味がありません。まず、数学(そして物理学)を教科書で勉強されることをお勧めします。(その前に「見えざる宇宙の形」や「エレガントな宇宙」を読む必要がありますね。)
最先端の物理学や数学は、(僕も含めてですが)教科書で勉強していない素人がいくら頭をひねっても理解できるものではありません。教科書や論文を何冊も読んで理解した上で、自分のアイデアや発想に意味をもたせることができるようになるものです。
原子レベルのテレポーテーションですが、僕のような素人が読めるレベルの教科書や科学教養書は販売されていません。以下のニュース記事で実験が成功したことを知っただけですので、詳細は全く知りません。ですのでブログに説明記事を書くこともできないわけです。その点、ご理解ください。
2004年
原子の量子テレポーテーションに成功(米国)
http://wiredvision.jp/lite/u/archives/200406/2004061801.html
http://japan.cnet.com/news/ent/story/0,2000056022,20069323,00.htm
原子レベルのテレポテーションが成功したという報告があるようですが。素粒子レベルのテレポテーションもありますよ。2つの電子が相互作用し互いに反対方向に飛んでいった場合1つの電子Aのスピンを観測した瞬間電子Bのスピンが変わる。またベルの不等式が成立しないことから非局所作用の存在が判りました。。つまりテレポテーションですね。これはポジトロニュウムという粒子から放出される光子のスピンを観測する実験です。
> カラビヤウ図形と言うものは余剰次元のコンパクト化されたものと考えれば一次元空間でも二次元空間でも存在するといえるのではないでしょうか?
カラビ-ヤウ図形は数学では複素数の次元で考えます。鈴木さまがおっしゃっているような実数の1次元や2次元のカラビ-ヤウ多様体は存在しません。
ウィキペディアを見ると、複素次元が1~3カラビ-ヤウ多様体についての記述があります。
複素次元が 1 の場合、コンパクトな唯一の例はトーラスであり、これは1-パラメーター族をなす。 トーラスのリッチ計量は実際、平坦計量であるので、ホロノミーは自明な群SU(1)である。 複素1次元カラビ・ヤウ多様体は複素楕円曲線であり、代数多様体である。
複素次元が 2 の場合は、K3曲面が唯一のコンパクトで単連結なカラビ・ヤウ多様体である。非単連結な例は、アーベル多様体により与えられる。エンリケス曲面と超楕円曲面は、第一チャーン類が実係数コホモロジー群の元としてはゼロになるが、整係数コホモロジー群の元としてはゼロにならず、リッチ計量の存在についてのヤウの定理を適用することはできるものの、カラビ・ヤウ多様体とは見なされないことが多い。アーベル曲面はカラビ・ヤウ多様体には分類しないことも多い。その理由は、ホロノミーが自明であり、SU(2)自体に同型となるのではなく、SU(2)の固有部分群となるからである。
複素次元が 3 の場合は、カラビ・ヤウ多様体の分類問題は未解決だが、有限個の族が存在するとヤウにより予想されている。ただし、その数は20年前に彼が見積もった数より遥かに大きくなる。さらには、マイルス・リード(Miles Reid)は、3次元カラビ・ヤウ多様体の位相的な種類が無限個あることを予想し、それらすべてを(たとえば、コニフォールド(conifold)のような)マイルドな特異性を通して、リーマン面で可能なように、連続的に変換することが可能なことも予想している複素3次元カラビ・ヤウ多様体の一つの例として、CP4の中の非特異なクインティックスリーフォールドは、CP4 の同次座標での同次 5次多項式のゼロ点からなる代数多様体がある。もう一つの例は、バース・ニエトの5次多様体のスムースなモデルである。クインティックスリーフォールドの Z5 作用による離散的な商もカラビ・ヤウ多様体となり、多くの文献で注目を集めている。これらうちの一つが、ミラー対称性 (弦理論)により、元々のクインティックスリーフォールドと関連付けられている。
カラビ-ヤウ図形についてのコメント受付は、いったん終了させていただきます。紹介させていただいた本をまずお読みください。お読みになってからでないと禅問答のようなことの繰り返しになってしまいますので。
> 原子レベルのテレポテーションが成功したという報告があるようですが。素粒子レベルのテレポテーションもありますよ。
はい、光子(素粒子)のテレポーテーションの成功のことは知っています。一般向けに解説した本もいくつかでていますね。立派な解説書ですので、僕がブログ記事でわざわざ解説記事を書く必要はありません。次のような記事で本を紹介しています。
再読:量子テレポーテーション:古澤明
http://blog.goo.ne.jp/ktonegaw/e/3612f0a3b86c8a8a247fe138f473adb3
量子光学と量子情報科学:古澤明
http://blog.goo.ne.jp/ktonegaw/e/dff342381e47d90aff6ed91edde198a8
ありがとうございました。
次元の数が実数でなく、複素数だというのはほとんどイメージできませんね。それは誰にとってもそうです。実数のように直線で座標軸を考えるのではなく、座標軸自体が実体のない a+bi のような複素数(この場合はガウス平面)が変化していくように値をとるわけですから。
複素数については高校数学で学ぶ範囲のことなので、ご存知だと思いますが、念のために解説ページを3つほど紹介しておきます。
http://atarimae.biz/archives/500
http://eman-physics.net/math/imaginary01.html
http://examist.jp/category/mathematics/complex-plane/
1.この多様体は検知できないくらい小さなものですか
2.この多様体によって私たちの周りの空間は埋め尽くされているのですか
3.2の場合私たちに多様体はどのような影響を与えているのですか
4、この多様体が存在することによって私たちの3次元空間は厚さを持つと考えてよろしいですか
以上よろしくお願いいたします。
カラビ-ヤウ図形についてのコメント受付は、いったん終了させていただきます。紹介させていただいた本をまずお読みください。お読みになってからでないと禅問答のようなことの繰り返しになってしまいますので。