
この実験のことは先日「力学系カオス: 松葉育雄」という本の紹介記事の最後で紹介したのだが、この本が専門書であるため、あまり読まれていない。
とても面白く、興味深い実験なので、できるだけ多くの人の目にとまるよう独立した記事として投稿させていただくことにした。
なお、カオス現象ではないが、磁石を使った実験では8年前に次の記事を書いている。
自由研究に「ガウス加速器」はいかが?
https://blog.goo.ne.jp/ktonegaw/e/6e9fe745f603c3ab42af3c21f1ef2ccb
また、磁石や磁力の発見の歴史に興味がある方は、次の本の紹介記事をお読みいただきたい。
磁力と重力の発見〈1〉古代・中世:山本義隆
https://blog.goo.ne.jp/ktonegaw/e/75ef1fc1216c255471fdbf65cc3a0c49
磁力と重力の発見〈2〉ルネサンス:山本義隆
https://blog.goo.ne.jp/ktonegaw/e/16b61843d410a867f942f3f8aef13865
磁力と重力の発見〈3〉近代の始まり:山本義隆
https://blog.goo.ne.jp/ktonegaw/e/196ce202408dd250728dad303dac89f3
「磁石振り子」によって現れるカオス軌道とフラクタル図形
本書で取り上げられている例は、どれも興味深いものだが、ひとつだけ紹介しておこう。「磁石振り子」によって現れるカオス軌道とフラクタル図形である。
まず、記事トップの画像のような装置を用意する。N極を上にした3つの磁石(赤、青、黄)を平面に固定し、上に鉄球(白)を振り子として吊るす。3つの磁石はどれも鉄球を引っ張っている状態だ。

磁石が1つしかないときは、磁場は(力が逆2乗の法則に従う)ニュートンの万有引力の法則のように円形になるはずだが、磁石が3つあるとそれぞれが反発しあうから、磁場すなわち磁力が等しい線(緑)と磁力線(赤)はこのような形になっているはずだ。(前野先生によるこのページをお借りして3つの正電荷の場合を想定して図を作成した。)

白球(鉄球)を横に引っ張って静止させ、手を離す。磁石がなければ通常の振り子の運動をするわけだが、磁石があるから白球は複雑な軌道で振れて、最後は3つの磁石のうちの1つに吸引されて止まる。
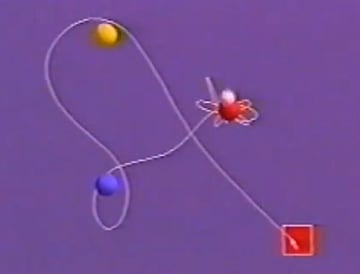
上の図は右下の赤い四角の位置で白球から手を離したときの図だ。複雑な軌道を描いてから、白球は赤い磁石で止まることを意味している。赤い磁石で止まったから、白球の初期位置を赤い四角に塗ったわけである。
同じことを白球の初期位置を変えて何度も行う。平面上は赤、青、黄の四角で塗りつぶされることになる。動画でご覧いただきたい。(再生時間7分)
カオス、フラクタルという数学と物理学の関係
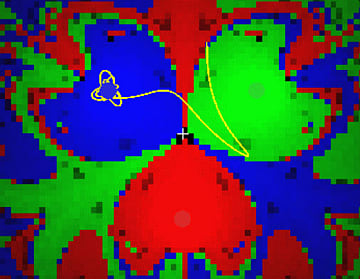
初期位置をわずかに変化させるだけで、軌道や最終位置が大きく変化することがおわかりになるだろう。これはカオス現象に必要な条件のひとつ「初期値鋭敏性」をあらわしている実験だ。最終的にこのような赤青黄が入り組んだ複雑な「フラクタル図形」が得られる。有名な「バタフライ効果」も初期値鋭敏性を示すカオス現象だ。
拡大

次のページではホームページに組み込まれたプログラムを使って、自分で実験することができる。初期位置にマウスポインタを置くと、白球が描く軌道がリアルタイムに描かれるので試していただきたい。(スマホではダメ。PCでのみ試せることを確認した。)
試してみる
この磁石振り子(magnet pendulum)はカオス現象の一例であり、(百円ショップで買える道具を使って)実際に実験できるだけでなく微分方程式をコンピュータで解いて得られる古典力学の問題であることを強調しておきたい。
教養書の紹介
カオスや力学系全般を数式なしで解説した教養書は、まだ読んでいないが、次のような本がよさそうである。ほかにお勧めの本をご存知の方は紹介していただきたい。
「カオス的世界像―非定形の理論から複雑系の科学へ: イアン スチュアート」(紹介記事)
「カオスとフラクタル (ちくま学芸文庫): 山口昌哉」


一風変わったところでは、この本が面白いかもしれない。
「カオスの紡ぐ夢の中で: 金子邦彦」

関連記事:
力学系カオス: 松葉育雄
https://blog.goo.ne.jp/ktonegaw/e/12392ac282d10deed28914d8182c2286
ポアンカレ 常微分方程式 -天体力学の新しい方法-
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/5c51d50e2141c8ae58c9323ad49b65a1
天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
数理解析のパイオニアたち: V.I.アーノルド
https://blog.goo.ne.jp/ktonegaw/e/165c894d023b1174fd519522935cdeeb
カオス的世界像―非定形の理論から複雑系の科学へ: イアン・スチュアート
https://blog.goo.ne.jp/ktonegaw/e/4ace135356ba99a1cb549bbbf073a591
メルマガを始めました。(目次一覧)

応援クリックをお願いします。







とても面白く、興味深い実験なので、できるだけ多くの人の目にとまるよう独立した記事として投稿させていただくことにした。
なお、カオス現象ではないが、磁石を使った実験では8年前に次の記事を書いている。
自由研究に「ガウス加速器」はいかが?
https://blog.goo.ne.jp/ktonegaw/e/6e9fe745f603c3ab42af3c21f1ef2ccb
また、磁石や磁力の発見の歴史に興味がある方は、次の本の紹介記事をお読みいただきたい。
磁力と重力の発見〈1〉古代・中世:山本義隆
https://blog.goo.ne.jp/ktonegaw/e/75ef1fc1216c255471fdbf65cc3a0c49
磁力と重力の発見〈2〉ルネサンス:山本義隆
https://blog.goo.ne.jp/ktonegaw/e/16b61843d410a867f942f3f8aef13865
磁力と重力の発見〈3〉近代の始まり:山本義隆
https://blog.goo.ne.jp/ktonegaw/e/196ce202408dd250728dad303dac89f3
「磁石振り子」によって現れるカオス軌道とフラクタル図形
本書で取り上げられている例は、どれも興味深いものだが、ひとつだけ紹介しておこう。「磁石振り子」によって現れるカオス軌道とフラクタル図形である。
まず、記事トップの画像のような装置を用意する。N極を上にした3つの磁石(赤、青、黄)を平面に固定し、上に鉄球(白)を振り子として吊るす。3つの磁石はどれも鉄球を引っ張っている状態だ。

磁石が1つしかないときは、磁場は(力が逆2乗の法則に従う)ニュートンの万有引力の法則のように円形になるはずだが、磁石が3つあるとそれぞれが反発しあうから、磁場すなわち磁力が等しい線(緑)と磁力線(赤)はこのような形になっているはずだ。(前野先生によるこのページをお借りして3つの正電荷の場合を想定して図を作成した。)

白球(鉄球)を横に引っ張って静止させ、手を離す。磁石がなければ通常の振り子の運動をするわけだが、磁石があるから白球は複雑な軌道で振れて、最後は3つの磁石のうちの1つに吸引されて止まる。

上の図は右下の赤い四角の位置で白球から手を離したときの図だ。複雑な軌道を描いてから、白球は赤い磁石で止まることを意味している。赤い磁石で止まったから、白球の初期位置を赤い四角に塗ったわけである。
同じことを白球の初期位置を変えて何度も行う。平面上は赤、青、黄の四角で塗りつぶされることになる。動画でご覧いただきたい。(再生時間7分)
カオス、フラクタルという数学と物理学の関係
初期位置をわずかに変化させるだけで、軌道や最終位置が大きく変化することがおわかりになるだろう。これはカオス現象に必要な条件のひとつ「初期値鋭敏性」をあらわしている実験だ。最終的にこのような赤青黄が入り組んだ複雑な「フラクタル図形」が得られる。有名な「バタフライ効果」も初期値鋭敏性を示すカオス現象だ。
拡大

次のページではホームページに組み込まれたプログラムを使って、自分で実験することができる。初期位置にマウスポインタを置くと、白球が描く軌道がリアルタイムに描かれるので試していただきたい。(スマホではダメ。PCでのみ試せることを確認した。)
試してみる

この磁石振り子(magnet pendulum)はカオス現象の一例であり、(百円ショップで買える道具を使って)実際に実験できるだけでなく微分方程式をコンピュータで解いて得られる古典力学の問題であることを強調しておきたい。
教養書の紹介
カオスや力学系全般を数式なしで解説した教養書は、まだ読んでいないが、次のような本がよさそうである。ほかにお勧めの本をご存知の方は紹介していただきたい。
「カオス的世界像―非定形の理論から複雑系の科学へ: イアン スチュアート」(紹介記事)
「カオスとフラクタル (ちくま学芸文庫): 山口昌哉」


一風変わったところでは、この本が面白いかもしれない。
「カオスの紡ぐ夢の中で: 金子邦彦」

関連記事:
力学系カオス: 松葉育雄
https://blog.goo.ne.jp/ktonegaw/e/12392ac282d10deed28914d8182c2286
ポアンカレ 常微分方程式 -天体力学の新しい方法-
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/5c51d50e2141c8ae58c9323ad49b65a1
天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
数理解析のパイオニアたち: V.I.アーノルド
https://blog.goo.ne.jp/ktonegaw/e/165c894d023b1174fd519522935cdeeb
カオス的世界像―非定形の理論から複雑系の科学へ: イアン・スチュアート
https://blog.goo.ne.jp/ktonegaw/e/4ace135356ba99a1cb549bbbf073a591
メルマガを始めました。(目次一覧)

応援クリックをお願いします。


























