複素数 a+bi のプラス記号は「足す」という意味？

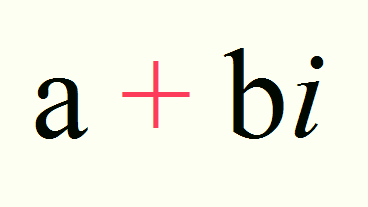
今回も虚数や複素数のことを学んだ高校生向けの記事。

私たちは小学校で足し算を学ぶ。プラスの数を足すと答は増えていく。

１＋１＝２、 ２＋１＝３、 ３＋１＝４ ...

この性質は分数や小数、そして中学校で学ぶ√２や√３などの無理数、そして一般に実数でも変わらない。（無理数どうしの足し算は１つの数としてあらわせないが、無限小数を使えば近似値として１つの数になる。）

こうして「＋」という記号は「プラスの量にプラスの量を足すことで量が増える。」という日常の実感に合った数学的操作であることを私たちは理解する。

ところが複素数はどうだろう？　前回の「虚数や複素数に大小がないのはなぜ？」という記事で虚数には大小という概念がないと証明したばかりだ。

「a と b 実数としたとき、そもそも a と bi を足してもよいのだろうか？」

それでは大きさのある実数と大きさの概念のない虚数を足すことになってしまう。もしそうしてもよいというのならそれはどういう意味なのだろうか？

先生に聞くと「それは足し算とは考えずに複素数はそのように表すのだよ。定義なのだよ。これで１つの数とみなすのだ。」とおっしゃるだろう。

みなさんはそれで納得されるのだろうか？　定義と言われれば証明する必要がない。どうもはぐらかされてしまったような気がしないだろうか？　どう見ても２つの数の和に見えてしまう。百歩譲ってこれが１つの数だと言うのなら、なぜわざわざプラス記号を間に入れるのだろう？

そして２つの複素数の足し算は次のように行う。a、b、c、dを実数としたとき複素数 a+bi と c+diの足し算は

a+bi + c+di　=　(a+c)　+　(b+d)i

のように計算する。左辺の２つの複素数の足し算の「＋」は、右辺で実数どうしの足し算の「＋」にするという計算に変化している。

足し算の記号「＋」を赤と青に色分けしておいた。青の計算は実数どうしの足し算だからOKである。しかし赤の計算は複素数どうしの足し算だ。この２つの足し算は明らかに違う種類のものである。同じ記号「＋」であらわしてよいのだろうか？問題は依然解決していない。


この疑問を解決するヒントになるのがハミルトンによる複素数の定義だ。ウィキペディアの「複素数」という項目には次のように書かれている。

1835年にハミルトンによって、負の数の平方根を用いない複素数の定義が与えられた。
実数の順序対 (a, b) および (c, d) に対して和と積を

(a, b) ＋ (c, d) = (a ＋ c, b ＋ d)
(a, b) × (c, d) = (ac － bd, ad ＋ bc)

により定めるとき、(a, b) を複素数という。実数 a は (a, 0) の形で表され、虚数単位 i は (0, 1) に当たる。

和だけに注目すれば、足し算記号「＋」の色分けによる区別は次のようになる。そしてこれは「定義」として与えられている。

(a, b) ＋ (c, d) = (a ＋ c, b ＋ d)

そうか、a+bi は (a, b) のようにあらわせばよいわけだな。これはまるでベクトルのようではないか！そして足し算、つまり和については２つの成分どうしを足すということまで複素数とベクトルは同じになっている。

実際、次の図を見ていただくとわかるように複素数の足し算とベクトルの足し算は、幾何的にまったく同じなので、２つの複素数、２つのベクトルの足し算をするためには、実数成分どうし、虚数成分どうしをそれぞれ足すということが共通しているのがわかる。

　

ベクトルの和もハミルトン流の複素数の和と同じ公式で計算できる。

(a, b) ＋ (c, d) = (a ＋ c, b ＋ d)

足し算記号「＋」があるときは、右辺でそれぞれX成分、Y成分の足し算「＋」として計算するのがベクトルの足し算のやり方だ。

これは「定義」ではあるけれども、上の図を見ると２つのベクトルそれぞれについてX軸、Y軸に垂線を下ろして原点を始点とする座標軸方向のベクトルを考えれば、X軸とY軸の数直線上の足し算になっていることによって説明がつく。

複素数の足し算も先ほどは「定義」だと言ったが、ベクトルの足し算の図と対応関係がまったく同じなので、２つの複素数、２つのベクトルの足し算をするために、実数成分どうし、虚数成分どうしをそれぞれ足すというのもベクトルの足し算のときと同じになる。

このようにベクトルの足し算で使う「＋」と複素数の足し算で使う「＋」は、同じ意味をもつ演算記号なのである。

a + bi

については、これをハミルトン流の表示

= (a, b)

であらわし、さらにこれを２つの複素数の和に分解する。そうすれば、この赤の「＋」がベクトルの足し算のように２成分をもつ数の足し算を意味するものであることが理解できるようになるだろう。

= (a, 0) + (0, b)

ベクトルや複素数の足し算は２成分の数をそれぞれ足す演算なので「＋」を使い、実数どうしの足し算は１成分の数を足す演算なので「＋」を使うわけだ。「＋」を使って足すときは「量が増える」が、「＋」を使う足し算では「量」という概念がない。

さらに行列どうしの足し算はどうだろう？ a～hを実数とし２行２列の行列どうしの足し算は次のように対応する成分どうしを足すことによって計算する。これは「定義」である。




けれども行列には４つの成分が含まれているから、これまでに紹介した実数どうし、複素数どうし、ベクトルどうしの足し算のどれとも意味が違う。だから足し算の記号も新しい色で書かなくてはならない。行列の足し算には緑色「＋」を使うことにしよう。




ベクトルは数を２成分に拡張したものであり、行列は４成分に拡張したものだ。このように足し算する対象を拡張するたびに足し算の意味が変わり、そのたびに新しい色で「＋」記号を書くのではきりがない。

また複素数は２行２列の行列によって表現することもできる。この場合複素数 a+bi の足し算記号も緑色の「＋」であらわすべきなのだろう。行列表現を使って複素数をあらわした場合でも足し算は４つの成分どうしの足し算になる。（参照：「複素数の行列表現」）



このように複素数はハミルトン流と行列流で表現することができるわけだが、どちらにしても小学校で習う足し算とは種類が違う。だからこのブログ記事ではこれまでに紹介した３つの種類（実数、複素数やベクトル、行列）の足し算をまとめて「加法」と呼ぶことにしよう。そして加法の計算をするときは黒の足し算記号「＋」を使うことにする。


ところで、中学の数学で「加法の法則」というのを学んでいたことを思い出してほしい。加法の法則は２つしかない。

[交換法則]　 ａ＋ｂ ＝ ｂ＋ａ
[結合法則] （ａ＋ｂ）＋ｃ ＝ ａ＋（ｂ＋ｃ）

この２つの法則を教科書で見たとき、僕は「なんて大げさだ。この２つが成り立つのは当たり前じゃん。」と思ったことを今でも覚えている。

けれども、この法則が示しているのはこの２つの式が実数だけでなく、複素数、ベクトル、行列でも成り立っているということなのだ。つまりこの法則の中で使われている「＋」記号は「＋」、「＋」、「＋」のどれでもよい。万能な加法の記号、黒の「＋」なのである。


そろそろこの記事の結論を書くときがきた。冒頭の問題を振り返ってみる。

「複素数 a+bi のプラス記号は「足す」という意味なのだろうか？」

プラスの記号が赤の足し算記号「＋」であることを説明した。けれどもこれまでの説明で、実数のとき量が増えるという意味の足し算「＋」、複素数やベクトルの足し算「＋」、行列の足し算「＋」などすべて含んだ万能な足し算のことを、このブログ記事では「加法」と呼び、黒の「＋」記号であらわすことにした。

この意味で複素数 a+bi のプラス記号は広い意味での「加法」の演算を意味しているというのが結論である。別の言い方をすれば、僕たちが小学校で習った足し算の記号「＋」は、高校数学で複素数、ベクトル、行列を学ぶ中で、より万能な加法の演算記号「＋」に変容していたわけなのだ。


このように数学では計算する対象や演算そのものを拡張していくことで、より一般的、抽象的な世界で成り立っている普遍的な法則や定理を貪欲に獲得していく。一般化を重ねるたびに数学はそのパワーと万能性を高めていくのだ。

加法の法則は単純すぎて取るに足らないものに思えるかもしれないが、加法だけでなく乗法も含めてベクトルや行列の法則を考えると、実数や複素数には見られない、より複雑な世界が現れ始めることは次のページでおわかりになるだろう。しかし、その複雑な広い世界はより単純な世界をその内に矛盾なく取り込んでいることを忘れてはならない。（参考記事：「複素世界は実世界とつながっている」）

ベクトルの内積（スカラー積）と外積（ベクトル積）の成分表示
http://fnorio.com/0126scalar_&_vector_product/scalar_&_vector_product.html

行列の基本的な性質
http://rikei-index.blue.coocan.jp/senkei/teigi1senkei.html


ベクトルと行列は大学の教養課程の「線形代数」という教科で、３次元以上の多次元に拡張される。またその成分は実数だけでなく複素数のものも扱う。そのようなベクトルと行列にはどのような法則が成り立つのだろうか？

また物理学科の３年次以降で学ぶ量子力学の世界は、無限次元の複素数ベクトルで張られる「ヒルベルト空間」という線形代数で記述することができる。ヒルベルト空間は量子力学にとっての舞台であり、それは数学で記述された仮想空間である。

みなさんが高校で学んでいる数学は、活躍の場が限りなく広がっていることがおわかりだろう。


応援クリックをお願いします！