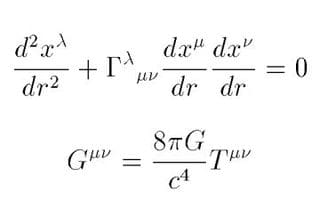
アインシュタインの一般相対性理論の敷居はずいぶん低くなっている。一般の人でも頑張れば数式を使った本来の意味で理解することができる状況なのだ。
掲載画像はこの理論を代表する2つの方程式。1916年に発表されたものだ。1つめは「測地線の方程式」と呼ばれている式で、物体の質量による重力によって曲げられた4次元の時空を進む光の軌跡をあらわしている。
2つめは「重力場の方程式」とか「アインシュタイン方程式」と呼ばれている式で、右辺の T であらわされる物質の質量(=エネルギー)や運動量によって左辺の G という「曲率」でその場所の時空がどのように曲げられるかを示している。時空の各点にこのような G と T が関連性をもちながら存在しているというのだ。2つめの式は次のように書かれる場合もある。
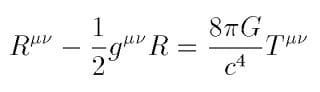
20世紀最高の科学者であるアインシュタイン。この理論を理解するためにはリーマン幾何学をはじめ、いくつかの高度な数学が必要になる。
天才の中の天才が発見したこの偉大な理論はとうてい自分には理解できないのだと最初からあきらめてしまってはいないだろうか? 凡人には天才のすごさは想像できても「天才の中の天才」のすごさとの違いはわからないのだと思っているのではないだろうか?
たしかに難しい理論である。しかしアインシュタインの感じたのはそれを「生み出す難しさ」であって「理解する難しさ」はその数百分の一以下であるはずだ。それに現代では理論は十分に研究され、数々の良書が手にはいる。
今日紹介するのは現時点においていちばん易しく楽しめる形で一般相対性理論を、その本来の数式の意味をそこなわずに理解できるようになるための手順だ。それもたった2冊の本を読むだけで事足りるのである。前提知識として高校レベルの数学の知識は必要であるが、それは「KIT数学ナビゲーション」のページでおさらいすればよいだけのこと。ベクトルと行列、微積分の単元を読んで理解すればよい。1週間もかければ十分だろう。
学生の諸君はこの夏休みに挑戦してみてはどうだろうか?この体験は人生においてお金では買うことのできない価値のひとつなのだと僕は思う。
もちろんこれに挑戦する人すべてが理解できるとは思っていない。独学で最終ゴールにたどりつける人の割合は、僕が想像するに次のような感じ。
- 中学時代に数学の平均点が40点くらいだった人:5%
- 中学時代に数学は得意ではなかったが授業にはついていけた人:10%
- 中学時代に数学は比較的得意だった人:20%
- 高校時代に数学は得意ではなかったが落ちこぼれていない人:30%
- 高校時代に数学の授業は3年生まで十分理解していた人:50%
- 理系学部の大学生(物理学専攻以外):70%
- 物理学専攻の大学生:85%
さて、最終ゴールにたどりつくための最短ルートを紹介しよう。学生時代のつまらない授業とは全く違った、想像力と知識欲に満たされた登山ルートだ。
大学レベルの物理数学のうち行列、ベクトル、微積分、一般座標変換(ヤコビアン)、ベクトル解析を理解する段階。これは登山にたとえれば、ふもとの山小屋でのトレーニングに相当する。
「図解入門 よくわかる物理数学の基本と仕組み」の第1章から第3章までを読んで理解しておけば十分である。実質140ページくらいの分量だ。Googleブック検索によるとこのようなレベルの本である。

もちろん、こちらのサイトで物理数学を学ぶのもよいと思う。
EMANの物理数学
http://eman-physics.net/math/contents.html
登山開始!「趣味で相対論」(Kindle版)という本を読むのがポイントだ。その内容はすべてネットで「EMANの相対性理論」として公開されている。

第1部「特殊相対論」
第1部「特殊相対性理論」を終えるまでが3合目あたり。なだらかな坂道なので楽しみながら読み進めることだろう。途中でマクスウェルの方程式に特殊相対論を適用するくだりがあるが、深く理解したい人は「EMANの電磁気学」や「趣味で物理学」の電磁気学についての章に寄り道するのもよい。
アインシュタイン自身、電磁気学的な発想で特殊相対性理論を導いている。だから特殊相対性理論は力学的な側面だけでなく光の速度と切り離せない電磁気学を学んでおくことは理にかなった寄り道なのだ。そもそも光は電磁波であり、原子は電子と原子核でできているのだから、物質現象の本質は電磁気の法則なのである。
第1部までの範囲で E=mc^2 の導き方は理解できるようになる。
第2部「座標変換の理論」
この章を登山にたとえるときつい上り坂だ。頑張って読み進もう。
相対性理論に座標変換は欠かせない。お互いの立場によって空間と時間の座標が異なっているからだ。時空が曲がっているというのはこのためである。お互いの間でどう見えるかは座標変換をしてみないと確認できない。
曲がった時空はいわばゆがんだ4次元方眼紙のようなもの。ゆがんだ方眼紙を時空の各点で拡大すると、それは「斜交座標」になる。普段私たちが使っている直交座標の軸を傾けたイメージだ。斜交座標には直交座標にはない「反変座標」と「共変座標」という2つの座標のとりかたがでてくる。これらがそれぞれお互いに離れた2人が自分の座標だと思っているものだ。(図版は「EMANの相対性理論」のこのページから拝借している。)

この2つの座標系で、ベクトルや行列を一般化した「テンソル」という量はそれぞれ「反変ベクトル」、「共変ベクトル」、「反変テンソル」、「共変テンソル」のようにあらわされ、「反変~」と「共変~」の間の変換式が紹介される。つまり微小な斜交空間どうして相手がお互いどう観測されるかが表現される。
テンソルというのは行列の一般化だと書いたが想像がつかないだろう。高校で習う行列は2行2列の行列でいわば「2次元の数」だ。これに「奥行き」の成分を加えて「2行2列2奥行き」のようにしたのが「3次元の数」でありこれを「3階のテンソル」と呼ぶ。つまり要素の数が i, j, k のように3つであらわされる「立体行列」のような量なのだ。たとえば物体に力がかかったとき内部に発生する張力や圧力、ひずみなどは「応力テンソル」という3行3列の2階テンソルであらわされる。(応力テンソルの解説を含むサイトのトップページはここ。)
相対性理論の時空は4次元だからテンソルの添え字の i, j, kのそれぞれは 0~3 の4つの値となる。つまり「4行4列4奥行き」のようなテンソルだ。実際のところはこれ以外のテンソルも出てくるので詳しいことは本で学んでほしい。
もうひとつ大切な量がある。「計量」や「計量テンソル」と呼ばれる4行4列の行列(2階テンソル)だ。これが時空の各点での斜交座標軸の「傾き方」を示している量だ。3次元の直交座標の場合、この計量テンソルは3次元の単位行列に一致する。計量はピタゴラスの定理やベクトルの内積の定義の一般化になっている。
ここまでの「座標変換の理論」は物理学ではなく数学の世界の話、幾何学の話である。
第3部「相対性原理の実践」
きつい上り坂はいったんここで終わる。5合目あたりだ。ここからは普通の斜面である。しかしこの章で解説される意味は重要なので気を抜かずにがんばろう。
ここではニュートン力学で使われていた質量、位置、速度、加速度、時間、エネルギー、運動方程式(F=ma)、電磁気学のマクスウェルの方程式などを相対論的な表現に書き換えておく。いわば一般相対論に入る前の物理学的な準備作業。
「相対論的な表現に書き換える」とは2つの座標系で物理法則が同じ形に表現されるように変えるということだ。そのことを「物理法則の共変性」とか「物理法則が共変的である」とか表現する。「共変ベクトル」のときの「共変」とは言葉は同じだが意味が異なる。つまり「相対性原理」とは物理法則の共変性のことである。
第4部「一般相対論の入り口」
この章のはじめが6合目あたり。ここから頂上まではまさに「絶壁」である。目がくらむが、読者をげんなりさせないために頂上からこの地点を見下ろしてくれている。頂上までの距離感をつかんでおくのは安心だ。
目標とする方程式は次の2つ。複雑なことをものすごく簡略化して表現している。
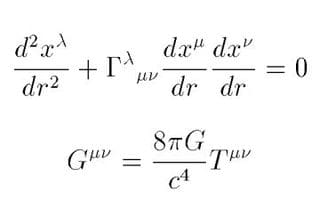
これらを分解して、どういうものが式に含まれているかを具体的に読者に紹介してくれている。結論だけ書いておこう。2つめの式、つまり重力場の方程式の展開はこのようになり、それに含まれるリッチ・テンソルの第1成分だけでもこのように展開されるものなのだ。
つまり一般相対性理論の方程式は、分解すればするほどわかりづらいものとなる。これを解決するのが「アインシュタインの縮約」と呼ばれる方法だ。この流儀のおかげで過度に式を複雑にしないまま計算を続けることができるのである。それでもなお式展開はこみいっているので、意味を深く考えずに数式の展開手順を丹念に追うことがこの絶壁を登るコツである。
第5部「リーマン幾何学」
微小な斜交座標がつながったのが曲線座標だ。相対性理論ではこの曲線座標は「4次元のゆがんだ方眼紙」である。ただこの中にいる人は自分が曲がった時空の中にいることには気がつかない。このように曲がった座標であらわされた幾何学をリーマン幾何学と呼んでいる。
私たちが習った「微分」は曲がった空間では成り立たない。微分とは少し離れた箇所との差を求めるのだから、座標が曲がっているとその結果は若干のずれを生じる。その補正をして微分をより完全にして一般化したのを「共変微分」と言う。つまりどのような座標系でも法則が変わらないような強力な微分なのだ。曲がった座標系では「平行移動」も直交座標系とは異なったものになる。曲がった時空を進む光のルート、すなわち「測地線」の方程式を得るのに平行移動は重要な考え方だ。
次に時空がどれほど曲がっているかを数式であらわすことを試みる。そのためにまず重要な考え方は「接続」や「接続係数」と呼ばれているものだ。時空のそれぞれの場所の斜交座標が連続的につながっていることが曲がった時空には必要だ。「接続」とはそのあたりのつながり具合をあらわす量。クリストッフェル記号であらわされる量である。テンソルの表現に似ているがテンソルの演算規則は満たしていない。
時空の曲がりを「接続」と「平行移動」の考え方を使ってあらわしたのが「リーマン曲率」だ一般相対性理論でいちばん難しいところ。これは「リーマン曲率テンソル」や「リーマン・テンソル」と呼ばれる量であらわされる。
リーマン・テンソルはあまりに複雑なので、これを縮約(単純化)したものを「リッチ・テンソル」と呼ぶ。これも時空の曲がり具合をあらわすテンソル量だ。「縮約」とはテンソルの階数を下げる数学演算である。
さらにリーマン・テンソルに計量テンソルを掛けることによって時空の曲がり具合は「リーマン曲率 R」と呼ばれるスカラー量になる。
またリーマン・テンソルは「ビアンキの恒等式」を使って「アインシュタイン・テンソル G」という時空の曲率をあらわすテンソルにまとめあげられる。
ここまでの説明は曲がった時空を表現するための数学的手法にすぎない。どうして時空が曲がるのかということについて何も言っていないからだ。物理学としての説明はここからはじまる。頂上は見えてきた。
まず、曲がった時空における測地線の方程式から近似的にニュートンの運動方程式(F=ma)が導けることを示す。
そして最終段階の「重力場の方程式」を導く。ここで「質量とエネルギーの等価原理」を導入する。「重力場の源はエネルギー運動量テンソルである」という考えを新しく採用することを意味する。 すると重力場の方程式の右辺は「エネルギーと運動量を含むテンソル T」となる。
つまり4次元時空の各点において方程式が
[時空の曲がりをあらわすテンソル]=比例定数x[エネルギーと運動量のテンソル]」
となった瞬間。右辺のエネルギーや運動量という物理的な量によって左辺の曲率という幾何学的な量が生じている。ゴールは目前だ!
仕上げにこの方程式の右辺に含まれる比例定数を求める。重力場の方程式を変形したものと、ニュートン力学から得られる「ポアソンの方程式」を比べてみると、この比例定数が万有引力の法則の「万有引力定数 G」であることがわかる。
ニュートン力学の重力ポテンシャルに対するポアソンの方程式

これで重力場の方程式は完全になった!これが一般相対性理論を制覇した瞬間である。
第6部「一般相対論の検証」
最後の章では「重力場の方程式の検証」を行う。詳細は省くが一般相対性理論の方程式から次のようなことが計算できることを具体的に見せてくれている。実際にそれらが理論だけから導かれる数式で表現されているのを目の当たりにすると、あらためてアインシュタインの先見性、洞察の深さに感動を覚えるのだ。
- ブラックホールの存在(シュバルツシルト解)
- 光の湾曲
- 水星の近日点移動
- 重力赤方偏移
以上が、これまで素人には理解できないと信じられてきた一般相対性理論の概要である。
なお、座標変換やリーマン幾何学など難しい数学の部分で途方にくれてしまった人には、もう少しわかりやすい本を紹介しておこう。
「相対性理論への数学的第一歩―共変微分のやさしい説明」

----------------------------
2011年11月7日に追記
その後、本書は改訂された。お買い求めになる方は新版をどうぞ。
「新版 相対性理論への数学的第一歩―共変微分のやさしい説明:多田知記」
----------------------------
2017年4月3日に追記
初学者が一般相対性理論に挑戦できる選択肢が増えた!
発売情報:一般相対性理論を一歩一歩数式で理解する: 石井俊全
https://blog.goo.ne.jp/ktonegaw/e/1699a1c22477c269c68c02091d0ca049
----------------------------
2018年12月22日に追記
初学者が一般相対性理論に挑戦できる選択肢がさらに増えた!
ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平
https://blog.goo.ne.jp/ktonegaw/e/f4401f2ce79451070b7b9c089f304315
----------------------------
2021年6月13日に追記
「ド文系」の著者が一般相対性理論を理解するに至ったドキュメンタリー本が講談社ブルーバックスから刊行された。
アインシュタイン方程式を読んだら「宇宙」が見えた:深川峻太郎
https://blog.goo.ne.jp/ktonegaw/e/4a200a8594234b351980a81062eec683
----------------------------




掲載画像はこの理論を代表する2つの方程式。1916年に発表されたものだ。1つめは「測地線の方程式」と呼ばれている式で、物体の質量による重力によって曲げられた4次元の時空を進む光の軌跡をあらわしている。
2つめは「重力場の方程式」とか「アインシュタイン方程式」と呼ばれている式で、右辺の T であらわされる物質の質量(=エネルギー)や運動量によって左辺の G という「曲率」でその場所の時空がどのように曲げられるかを示している。時空の各点にこのような G と T が関連性をもちながら存在しているというのだ。2つめの式は次のように書かれる場合もある。
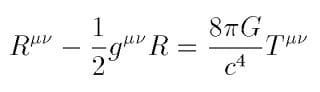
20世紀最高の科学者であるアインシュタイン。この理論を理解するためにはリーマン幾何学をはじめ、いくつかの高度な数学が必要になる。
天才の中の天才が発見したこの偉大な理論はとうてい自分には理解できないのだと最初からあきらめてしまってはいないだろうか? 凡人には天才のすごさは想像できても「天才の中の天才」のすごさとの違いはわからないのだと思っているのではないだろうか?
たしかに難しい理論である。しかしアインシュタインの感じたのはそれを「生み出す難しさ」であって「理解する難しさ」はその数百分の一以下であるはずだ。それに現代では理論は十分に研究され、数々の良書が手にはいる。
今日紹介するのは現時点においていちばん易しく楽しめる形で一般相対性理論を、その本来の数式の意味をそこなわずに理解できるようになるための手順だ。それもたった2冊の本を読むだけで事足りるのである。前提知識として高校レベルの数学の知識は必要であるが、それは「KIT数学ナビゲーション」のページでおさらいすればよいだけのこと。ベクトルと行列、微積分の単元を読んで理解すればよい。1週間もかければ十分だろう。
学生の諸君はこの夏休みに挑戦してみてはどうだろうか?この体験は人生においてお金では買うことのできない価値のひとつなのだと僕は思う。
もちろんこれに挑戦する人すべてが理解できるとは思っていない。独学で最終ゴールにたどりつける人の割合は、僕が想像するに次のような感じ。
- 中学時代に数学の平均点が40点くらいだった人:5%
- 中学時代に数学は得意ではなかったが授業にはついていけた人:10%
- 中学時代に数学は比較的得意だった人:20%
- 高校時代に数学は得意ではなかったが落ちこぼれていない人:30%
- 高校時代に数学の授業は3年生まで十分理解していた人:50%
- 理系学部の大学生(物理学専攻以外):70%
- 物理学専攻の大学生:85%
さて、最終ゴールにたどりつくための最短ルートを紹介しよう。学生時代のつまらない授業とは全く違った、想像力と知識欲に満たされた登山ルートだ。
大学レベルの物理数学のうち行列、ベクトル、微積分、一般座標変換(ヤコビアン)、ベクトル解析を理解する段階。これは登山にたとえれば、ふもとの山小屋でのトレーニングに相当する。
「図解入門 よくわかる物理数学の基本と仕組み」の第1章から第3章までを読んで理解しておけば十分である。実質140ページくらいの分量だ。Googleブック検索によるとこのようなレベルの本である。

もちろん、こちらのサイトで物理数学を学ぶのもよいと思う。
EMANの物理数学
http://eman-physics.net/math/contents.html
登山開始!「趣味で相対論」(Kindle版)という本を読むのがポイントだ。その内容はすべてネットで「EMANの相対性理論」として公開されている。

第1部「特殊相対論」
第1部「特殊相対性理論」を終えるまでが3合目あたり。なだらかな坂道なので楽しみながら読み進めることだろう。途中でマクスウェルの方程式に特殊相対論を適用するくだりがあるが、深く理解したい人は「EMANの電磁気学」や「趣味で物理学」の電磁気学についての章に寄り道するのもよい。
アインシュタイン自身、電磁気学的な発想で特殊相対性理論を導いている。だから特殊相対性理論は力学的な側面だけでなく光の速度と切り離せない電磁気学を学んでおくことは理にかなった寄り道なのだ。そもそも光は電磁波であり、原子は電子と原子核でできているのだから、物質現象の本質は電磁気の法則なのである。
第1部までの範囲で E=mc^2 の導き方は理解できるようになる。
第2部「座標変換の理論」
この章を登山にたとえるときつい上り坂だ。頑張って読み進もう。
相対性理論に座標変換は欠かせない。お互いの立場によって空間と時間の座標が異なっているからだ。時空が曲がっているというのはこのためである。お互いの間でどう見えるかは座標変換をしてみないと確認できない。
曲がった時空はいわばゆがんだ4次元方眼紙のようなもの。ゆがんだ方眼紙を時空の各点で拡大すると、それは「斜交座標」になる。普段私たちが使っている直交座標の軸を傾けたイメージだ。斜交座標には直交座標にはない「反変座標」と「共変座標」という2つの座標のとりかたがでてくる。これらがそれぞれお互いに離れた2人が自分の座標だと思っているものだ。(図版は「EMANの相対性理論」のこのページから拝借している。)

この2つの座標系で、ベクトルや行列を一般化した「テンソル」という量はそれぞれ「反変ベクトル」、「共変ベクトル」、「反変テンソル」、「共変テンソル」のようにあらわされ、「反変~」と「共変~」の間の変換式が紹介される。つまり微小な斜交空間どうして相手がお互いどう観測されるかが表現される。
テンソルというのは行列の一般化だと書いたが想像がつかないだろう。高校で習う行列は2行2列の行列でいわば「2次元の数」だ。これに「奥行き」の成分を加えて「2行2列2奥行き」のようにしたのが「3次元の数」でありこれを「3階のテンソル」と呼ぶ。つまり要素の数が i, j, k のように3つであらわされる「立体行列」のような量なのだ。たとえば物体に力がかかったとき内部に発生する張力や圧力、ひずみなどは「応力テンソル」という3行3列の2階テンソルであらわされる。(応力テンソルの解説を含むサイトのトップページはここ。)
相対性理論の時空は4次元だからテンソルの添え字の i, j, kのそれぞれは 0~3 の4つの値となる。つまり「4行4列4奥行き」のようなテンソルだ。実際のところはこれ以外のテンソルも出てくるので詳しいことは本で学んでほしい。
もうひとつ大切な量がある。「計量」や「計量テンソル」と呼ばれる4行4列の行列(2階テンソル)だ。これが時空の各点での斜交座標軸の「傾き方」を示している量だ。3次元の直交座標の場合、この計量テンソルは3次元の単位行列に一致する。計量はピタゴラスの定理やベクトルの内積の定義の一般化になっている。
ここまでの「座標変換の理論」は物理学ではなく数学の世界の話、幾何学の話である。
第3部「相対性原理の実践」
きつい上り坂はいったんここで終わる。5合目あたりだ。ここからは普通の斜面である。しかしこの章で解説される意味は重要なので気を抜かずにがんばろう。
ここではニュートン力学で使われていた質量、位置、速度、加速度、時間、エネルギー、運動方程式(F=ma)、電磁気学のマクスウェルの方程式などを相対論的な表現に書き換えておく。いわば一般相対論に入る前の物理学的な準備作業。
「相対論的な表現に書き換える」とは2つの座標系で物理法則が同じ形に表現されるように変えるということだ。そのことを「物理法則の共変性」とか「物理法則が共変的である」とか表現する。「共変ベクトル」のときの「共変」とは言葉は同じだが意味が異なる。つまり「相対性原理」とは物理法則の共変性のことである。
第4部「一般相対論の入り口」
この章のはじめが6合目あたり。ここから頂上まではまさに「絶壁」である。目がくらむが、読者をげんなりさせないために頂上からこの地点を見下ろしてくれている。頂上までの距離感をつかんでおくのは安心だ。
目標とする方程式は次の2つ。複雑なことをものすごく簡略化して表現している。
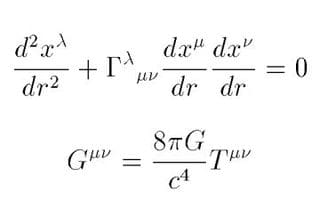
これらを分解して、どういうものが式に含まれているかを具体的に読者に紹介してくれている。結論だけ書いておこう。2つめの式、つまり重力場の方程式の展開はこのようになり、それに含まれるリッチ・テンソルの第1成分だけでもこのように展開されるものなのだ。
つまり一般相対性理論の方程式は、分解すればするほどわかりづらいものとなる。これを解決するのが「アインシュタインの縮約」と呼ばれる方法だ。この流儀のおかげで過度に式を複雑にしないまま計算を続けることができるのである。それでもなお式展開はこみいっているので、意味を深く考えずに数式の展開手順を丹念に追うことがこの絶壁を登るコツである。
第5部「リーマン幾何学」
微小な斜交座標がつながったのが曲線座標だ。相対性理論ではこの曲線座標は「4次元のゆがんだ方眼紙」である。ただこの中にいる人は自分が曲がった時空の中にいることには気がつかない。このように曲がった座標であらわされた幾何学をリーマン幾何学と呼んでいる。
私たちが習った「微分」は曲がった空間では成り立たない。微分とは少し離れた箇所との差を求めるのだから、座標が曲がっているとその結果は若干のずれを生じる。その補正をして微分をより完全にして一般化したのを「共変微分」と言う。つまりどのような座標系でも法則が変わらないような強力な微分なのだ。曲がった座標系では「平行移動」も直交座標系とは異なったものになる。曲がった時空を進む光のルート、すなわち「測地線」の方程式を得るのに平行移動は重要な考え方だ。
次に時空がどれほど曲がっているかを数式であらわすことを試みる。そのためにまず重要な考え方は「接続」や「接続係数」と呼ばれているものだ。時空のそれぞれの場所の斜交座標が連続的につながっていることが曲がった時空には必要だ。「接続」とはそのあたりのつながり具合をあらわす量。クリストッフェル記号であらわされる量である。テンソルの表現に似ているがテンソルの演算規則は満たしていない。
時空の曲がりを「接続」と「平行移動」の考え方を使ってあらわしたのが「リーマン曲率」だ一般相対性理論でいちばん難しいところ。これは「リーマン曲率テンソル」や「リーマン・テンソル」と呼ばれる量であらわされる。
リーマン・テンソルはあまりに複雑なので、これを縮約(単純化)したものを「リッチ・テンソル」と呼ぶ。これも時空の曲がり具合をあらわすテンソル量だ。「縮約」とはテンソルの階数を下げる数学演算である。
さらにリーマン・テンソルに計量テンソルを掛けることによって時空の曲がり具合は「リーマン曲率 R」と呼ばれるスカラー量になる。
またリーマン・テンソルは「ビアンキの恒等式」を使って「アインシュタイン・テンソル G」という時空の曲率をあらわすテンソルにまとめあげられる。
ここまでの説明は曲がった時空を表現するための数学的手法にすぎない。どうして時空が曲がるのかということについて何も言っていないからだ。物理学としての説明はここからはじまる。頂上は見えてきた。
まず、曲がった時空における測地線の方程式から近似的にニュートンの運動方程式(F=ma)が導けることを示す。
そして最終段階の「重力場の方程式」を導く。ここで「質量とエネルギーの等価原理」を導入する。「重力場の源はエネルギー運動量テンソルである」という考えを新しく採用することを意味する。 すると重力場の方程式の右辺は「エネルギーと運動量を含むテンソル T」となる。
つまり4次元時空の各点において方程式が
[時空の曲がりをあらわすテンソル]=比例定数x[エネルギーと運動量のテンソル]」
となった瞬間。右辺のエネルギーや運動量という物理的な量によって左辺の曲率という幾何学的な量が生じている。ゴールは目前だ!
仕上げにこの方程式の右辺に含まれる比例定数を求める。重力場の方程式を変形したものと、ニュートン力学から得られる「ポアソンの方程式」を比べてみると、この比例定数が万有引力の法則の「万有引力定数 G」であることがわかる。
ニュートン力学の重力ポテンシャルに対するポアソンの方程式

これで重力場の方程式は完全になった!これが一般相対性理論を制覇した瞬間である。
第6部「一般相対論の検証」
最後の章では「重力場の方程式の検証」を行う。詳細は省くが一般相対性理論の方程式から次のようなことが計算できることを具体的に見せてくれている。実際にそれらが理論だけから導かれる数式で表現されているのを目の当たりにすると、あらためてアインシュタインの先見性、洞察の深さに感動を覚えるのだ。
- ブラックホールの存在(シュバルツシルト解)
- 光の湾曲
- 水星の近日点移動
- 重力赤方偏移
以上が、これまで素人には理解できないと信じられてきた一般相対性理論の概要である。
なお、座標変換やリーマン幾何学など難しい数学の部分で途方にくれてしまった人には、もう少しわかりやすい本を紹介しておこう。
「相対性理論への数学的第一歩―共変微分のやさしい説明」

----------------------------
2011年11月7日に追記
その後、本書は改訂された。お買い求めになる方は新版をどうぞ。
「新版 相対性理論への数学的第一歩―共変微分のやさしい説明:多田知記」
----------------------------
2017年4月3日に追記
初学者が一般相対性理論に挑戦できる選択肢が増えた!
発売情報:一般相対性理論を一歩一歩数式で理解する: 石井俊全
https://blog.goo.ne.jp/ktonegaw/e/1699a1c22477c269c68c02091d0ca049
----------------------------
2018年12月22日に追記
初学者が一般相対性理論に挑戦できる選択肢がさらに増えた!
ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平
https://blog.goo.ne.jp/ktonegaw/e/f4401f2ce79451070b7b9c089f304315
----------------------------
2021年6月13日に追記
「ド文系」の著者が一般相対性理論を理解するに至ったドキュメンタリー本が講談社ブルーバックスから刊行された。
アインシュタイン方程式を読んだら「宇宙」が見えた:深川峻太郎
https://blog.goo.ne.jp/ktonegaw/e/4a200a8594234b351980a81062eec683
----------------------------




























超弦理論については大栗先生の本のほか、入門レベルの教科書「初級講座弦理論 基礎編、発展編:B.ツヴィーバッハ」などを読みました。肯定派か否定派かということでは8割肯定派ということろでしょうか。
初級講座弦理論 基礎編、発展編:B.ツヴィーバッハ
http://blog.goo.ne.jp/ktonegaw/e/6da996449afaf50f8cf0f4f84881da0e
http://blog.goo.ne.jp/ktonegaw/e/ff65ac32a5a9b397d8833a7ca155cb68
カラビ-ヤウ空間のこと自体まで僕の理解が進んでいませんし、pブレーンやDブレーンになると「本当かなぁ??」とも思えてしまうわけです。ただし、重力と量子力学を矛盾なく満たすこと、素粒子の標準理論を含んでいることは実際に理解して驚きました。しかし、まだ生まれたばかりの理論ですから、これからということでしょうね。どのように発展していくのかさまざまな可能性があるはずです。
宇宙戦艦ヤマトの新作は面白そうですね。予告編などチェックしてみます。
ラグランジアンは(超弦理論でない)通常の物理学の範囲でしたら理解していますよ。「物理数学の直観的方法」や「EMANの解析力学」をお読みになるのが手っ取り早いと思います。
物理数学の直観的方法
http://blog.goo.ne.jp/ktonegaw/e/ab9396e295687179ac3a71553b8165a1
EMANの解析力学
http://homepage2.nifty.com/eman/analytic/contents.html
とねさんは超弦理論はどうおもわれますか?
私は肯定派なんですが今だ実験で証明されていないのが現状で残念です。余次元はカラビヤウ空間にまとめられてると11次元とか、M理論とかメンブレーンの存在についてもあくまでも理論上の話で今だ実験物理では避難中傷をあびています。宇宙戦艦ヤマトはほんと私の原点で、いまリメイクで2199が人気があります劇場公開も12月6日にありイスカンダルから帰るところから話が出てきます。ちゃんと物理の話があるので、臨場感が
ありほんにおもしろいですよ!!重力勾配とか、ラグランジュポイントL1とかかなりリアルあるです。ラグランジュ方程式一応解けるんですけど11次元のラグラジアンンはさすがに解けません。とねさんはわかりますか?
はじめまして。コメントをいただきありがとうございました。
この記事を書いたのは5年前ですが、当時のgooブログでは1つの記事に入力できる文字数が今より少なかったので、一般相対論を手短かにまとめるのに苦労したことを思い出しました。簡潔に説明しているのはそのせいかもしれません。
僕も昔は天文学に熱中していた時期がありました。ブログを拝見させていただいたところ、趣味が実に多彩ですね。ドブソニアンの望遠鏡は僕が高校生の頃に販売されるようになりました。今も昔も天体望遠鏡は高価ですね。w
あとお若い方も宇宙戦艦ヤマトが好きな方もかなり多くいることに、リアルタイムで初代宇宙戦艦ヤマトのテレビ放送や映画を見ていた僕としては感慨深いものがあります。
を大学で勉強してまして、とくに宇宙や星が好きです。宇宙がなぜ始まったのか重力の正体とは?数式は自然を記述する道具だけれども、私はそこに哲学てきなものがはいりこんでいると思うのです。理由は微細構造定数とか1/137
絶妙な天体の動き方とかほんまに絶妙なタイミングと数値(定数)で私たちはこの地球にすんでいるからです。
英語の物理フォーラムにお考えを投稿されていたのですね。すごいなーと思います。僕などとてもそんな勇気はありません。(笑)
そのように叩かれながら成長するということも考えられますけど、趣味でされているのなら楽しいほうがいいですよね。
世の中いろいろな人がいますし、お互い顔の見えない状況での議論になりますので気をつけてください。
これからもよろしくお願いします。
暖かいお言葉、有り難うございます。
物理学関係で投稿したりメールしたりしても、けんもほろろな扱いを受けることが多く、少しへこんでいました。
http://www.physicsforums.com/showthread.php?p=4525789&posted=1#post4525789
などは、至極真っ当な主張をしたつもりだったのですが。
これからもよろしくお願いいたします。
http://doppolaboratory.com/
Sorao
はじめまして。コメントをいただきありがとうございます。
素敵なホームページですね。拝見させていただきました。英語メニューもお作りになっているところから「意欲」が強く伝わってきました。(アメリカ国旗ではなくイギリス国旗なのですね。)
僕もこのようなホームページを作りたいと数年前から思っているのですが、時間がとれずに実現していません。
「空男の物理学」の内容が着実に増えていくことを楽しみにしています。ときどき訪問させていただきます。
Sorao(本名:安井克明)と言います。
私も一般相対性理論に挑戦中です。 いろいろな教科書に挑戦しては挫折して次の教科書を探す、と言う行動を繰り返していたのですが、このページで紹介されている本は良いですね。 特に、EMANさんの本は、普通の教科書には無い、納得できる深掘りがされており、私の第1のおすすめです。
おかげで、Schwarzschild時空については、ほぼ理解できたと思っております。 下記ホームページの、「Excelを用いた Schwarzschild 時空の具体例計算」 にまとめましたので、よろしければ一度ご訪問下さい。
http://doppolaboratory.com/
Sorao
コメントいただき、ありがとうございました。
大畠様からコメントいただいた文面の最後のほうに大畠様の(フリーアドレスではない正式の)メールアドレスが記載されていましたので、そのままコメント公開してしまうとご迷惑になると思い、メールアドレスを表示しない文面に変更して私のほうで再投稿させていただきました。
さて、コメントいただいた内容についてですが、ほとんどの物理学者に受け入れられている一般相対性理論に誤りが含まれているという主張に同意するのは勇気がいることであり、慎重に考えなければなりません。
少しお時間をいただきますようお願いします。
また、僕は専門の研究者ではなく、ただの物理学好きな素人ですので大畠様のお考えの内容を理解できるかどうかは今のところわかりません。
より知識のある多くの方の考えを聞くのには「EMANの物理学」というサイトの掲示板が知られていますが、そちらにご自身の考えを述べてみてはいかがでしょうか?
拝啓 「とね日記」を拝見いたしました。
一般相対性理論における、次のような問題(誤り)を示しましたので、お知らせいたします。
問題.
1.重力赤方偏移が教科書によって、縦ドップラー効果で説明されているものと、横ドップラー効果で説明されているもの(など)とありますが、二つのドップラー効果は物理的意味が全く異なるものです。従って、二通り(以上)に説明されていることはおかしい。
2.一般相対性理論で、シュワルツシルト時空(例えば太陽系)に於いて、空間半径方向に(人間の目の前の短い長さでさえ)一本の物指の長さが二つ以上あることは矛盾である。
3.シュワルツシルト表面が、物理学理論上の“実在”である事象の地平面であり、かつもう一方で(人間の机上の式計算である)一般座標変換で生じたり消滅したりするみかけの特異点(面)でもあることは矛盾である。
これらの問題(誤り)及び解決について、ホームページ『一般相対性理論の誤りについて』(添付ファイル)で述べましたので、是非ご覧になってください。
ホームページURLは https://sites.google.com/site/oohatarelativity/ です。ホームページの ご意見・ご感想はこちらまで のこちらをクリックすると大畠までメールを送ることができます。
ご多忙中と存じますが、ご意見・ご感想を下さいませんでしょうか。ご面倒と思いますが、問題の1.~3.について、はい、いいえ でお答え下さいませんでしょうか。
(ホームページから大畠にメールを送ることができます。)
よろしくお願いいたします。
敬具
2012年5月27日 大畠哲也.
そうなのです。特殊相対性理論は数学好きな高校生のレベルであれば理解できますよね。
「一般」のほうは、だいぶ敷居が下がったもののゴールに到達できる人は少ないかもしれません。それでもEMANさんの取り組みはすばらしいと僕は思っています。
> 大学の数学は概念と記号が多いだけで、
> 計算自体は中学高校の時よりも遥かに
> 簡単ですから。
なるほど、そういう考え方もありますね。納得しました。
僕自身も難関校の入学試験の数学や数学オリンピックの問題で、解けないものがたくさんあります。
なんだか眠れなくてネットをつらつらと見ていたところとねさんのHPを発見、触発されて特殊相対論を調べてたらこんな時間に^^;
特殊相対論は意外と簡単ですね。これなら一般相対論も楽勝・・・と思ったら特殊は「なだらかな坂」で一般は「絶壁」ですか^^;;;
独学でゴールにたどり着ける人の節ですが、相対論で使ってる数学は大学の数学みたいなので中学高校の数学の点数はあてにならないと思いますよ。大学の数学は概念と記号が多いだけで、計算自体は中学高校の時よりも遥かに簡単ですから。