式の計算で、どういうわけか 同じパターンのミスを見かけます。
たくさんの人が同じパターンで間違えるというのは
授業のどこかで、大きな勘違いを誘発しているのでは?と推測します。
たとえば次のような 問題

分数の割り算は、分数の分母と分子をひっくり返して(逆数にして)
逆数のかけ算になおして計算する。という方法がありました。
そのやり方で解いたら上のようになった!
このように考える方が多数います。
なるほど分数はひっくり返っているように見えますが
分数の一部しかひっくり返っていない!のです

このようにABを分子側に仕分けしてから上下をひっくり返しますと
間違えずに計算できます。
そして、符号ですが
×と-は、並べて書けない!(これがあまり伝わっていません)
式の中に符号(特にマイナス)が入っているときは
符号の計算を先にして、この式はプラスになるのか?マイナスになるのか?
先に書いておくと、後は符号を考えずに計算できますね。
今回は、計算結果は符号がプラスになりますから

となって、後は約分して整理します。
解き方にもパターンがありますが、
間違い方にも パターンがあります。
どちらも経験し、理解できますと 正確な計算ができるようになります。
===================================
前回の課題

ふたつの抵抗が並列に接続された場合の
抵抗の合計Rは?
電圧をE(v)、抵抗R1(Ω)、抵抗R2(Ω)、
R1に流れる電流 i1(A) R2に流れる電流 i2(A) とすると
いいですか?いっきに書きますと
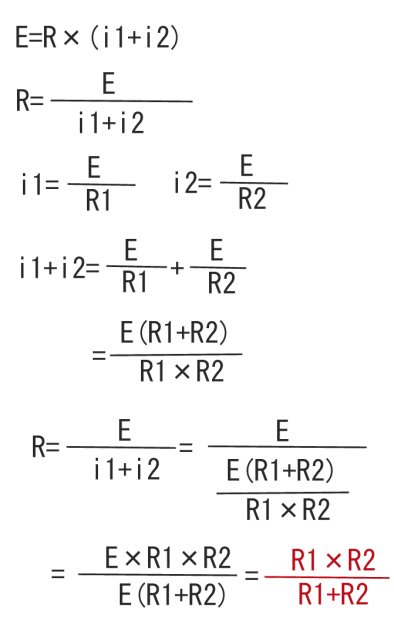
となります。
習った公式と一緒でしょ?
理科っていうより、まるまる数学ですね~
ただ、理科が数学と違うのは
計算通りにいかないことが多々ある!ということです。
原発も計算上では、事故は起こらないことになっていますから。









