[問題]
熊本県中学校数学教育研究会編「数学の友1年」啓林館版より。単元"角柱、円柱の表面積"のP.79[3]です。一部変更。
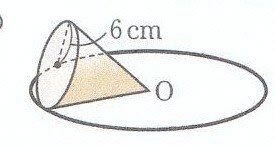
図のように、底面の半径が6cmの円錐を、頂点Oを中心として平面上で転がしたところ、もとの位置にもどるのに、円錐は3回転した。次の問いに答えなさい。
(1)円錐の母線の長さを求めなさい。
(2)円錐の表面積を求めなさい。
(1)の解説解答は、こちら。
(2)を解きます。
(1)で求めた、円すいの母線 = 18(cm)も使います。図に書き込んで確認をしましょう。(1)だけ特に与えられた条件がなければ、(2)以降でも「(1)より」と使っていいのです。
[接(せっ)した図形のルール]
"接した線分は、それぞれおなじ長さです。"
当たり前ですね。数学は、当たり前のルールをどんな場合でも使えるようていねいに説明しているだけですから。
[立体のルール]
角柱、円柱、角すい、円すい、は「立体」です。立体の問題は、「体積」と「表面積」。問題文からまず、"なにを求めるか"を確認します。たいてい、問題文の最後に書かれています。
「表面積」は、cm^2(平方センチメートル)。2乗=「平方」のこと。⇒「立体の表面積」は、面積ですから「展開図」を描いて平面に分けます。⇒円すいの表面積なら、「底面の円+側面のおうぎ形」を描きます。
描いた図に、長さや角度といった問題文から読み取れる「数字」と求める辺や角を「文字」で書き込みます。問題文にもどらず、"図を使って"理解し解いていきます。絵や図やグラフは、ヒトの直感にうったえかけ、"ひらめき"を生むからです。
図形問題はなんのため?|熊本県公立高校後期試験
[円の面積と円周のルール]
円の公式は、「円の面積」と。「円周」ですね。単位もつけて覚えればまちがえません。
円の面積(cm^2) = πr^2
円周の長さ(cm) = 2πr
[表面積のルール]
立体の表面積は、「底面積+側面石」です。
底面積 : πr^2 = π×6^2 = 36π(cm^2)
側面積 :
例題のように、「底面の円周」と「側面のおうぎ形の弧(こ・曲線部分)」が接していて長さが等(ひと)しいことを利用し、おうぎ形の中心角をx°とおいて解きます。
別解を。
この円すいの側面は、大きな円に接して3回転しています。接しているので…
[接(せっ)した図形のルール]
"接した面は、それぞれおなじ面積です。"
大きな円の面積は、円すいの側面積の3回転分と等(ひと)しい。つまり、円すいの側面積は大きな円の面積の三分の一です!
側面積 : π× 18^2 × 1/3 = 108π(cm^2)
表面積=底面積+側面積をわすれずに!
36π+ 108π = 144π(cm^2)
ルールさえわかれば、計算はやっぱりかんたん。
よのなかはルールでできています。数(かず)のルールを利用し、言葉にたよらず図で理解や説明をするトレーニングが図形問題なんです。(塾長)
たくさんの情報は整理をしよう|ヒトのもつチカラ、「書く」チカラ
熊本県中学校数学教育研究会編「数学の友1年」啓林館版より。単元"角柱、円柱の表面積"のP.79[3]です。一部変更。
図のように、底面の半径が6cmの円錐を、頂点Oを中心として平面上で転がしたところ、もとの位置にもどるのに、円錐は3回転した。次の問いに答えなさい。
(1)円錐の母線の長さを求めなさい。
(2)円錐の表面積を求めなさい。
(1)の解説解答は、こちら。
(2)を解きます。
(1)で求めた、円すいの母線 = 18(cm)も使います。図に書き込んで確認をしましょう。(1)だけ特に与えられた条件がなければ、(2)以降でも「(1)より」と使っていいのです。
[接(せっ)した図形のルール]
"接した線分は、それぞれおなじ長さです。"
当たり前ですね。数学は、当たり前のルールをどんな場合でも使えるようていねいに説明しているだけですから。
[立体のルール]
角柱、円柱、角すい、円すい、は「立体」です。立体の問題は、「体積」と「表面積」。問題文からまず、"なにを求めるか"を確認します。たいてい、問題文の最後に書かれています。
「表面積」は、cm^2(平方センチメートル)。2乗=「平方」のこと。⇒「立体の表面積」は、面積ですから「展開図」を描いて平面に分けます。⇒円すいの表面積なら、「底面の円+側面のおうぎ形」を描きます。
描いた図に、長さや角度といった問題文から読み取れる「数字」と求める辺や角を「文字」で書き込みます。問題文にもどらず、"図を使って"理解し解いていきます。絵や図やグラフは、ヒトの直感にうったえかけ、"ひらめき"を生むからです。
図形問題はなんのため?|熊本県公立高校後期試験
[円の面積と円周のルール]
円の公式は、「円の面積」と。「円周」ですね。単位もつけて覚えればまちがえません。
円の面積(cm^2) = πr^2
円周の長さ(cm) = 2πr
[表面積のルール]
立体の表面積は、「底面積+側面石」です。
底面積 : πr^2 = π×6^2 = 36π(cm^2)
側面積 :
例題のように、「底面の円周」と「側面のおうぎ形の弧(こ・曲線部分)」が接していて長さが等(ひと)しいことを利用し、おうぎ形の中心角をx°とおいて解きます。
別解を。
この円すいの側面は、大きな円に接して3回転しています。接しているので…
[接(せっ)した図形のルール]
"接した面は、それぞれおなじ面積です。"
大きな円の面積は、円すいの側面積の3回転分と等(ひと)しい。つまり、円すいの側面積は大きな円の面積の三分の一です!
側面積 : π× 18^2 × 1/3 = 108π(cm^2)
表面積=底面積+側面積をわすれずに!
36π+ 108π = 144π(cm^2)
ルールさえわかれば、計算はやっぱりかんたん。
よのなかはルールでできています。数(かず)のルールを利用し、言葉にたよらず図で理解や説明をするトレーニングが図形問題なんです。(塾長)
たくさんの情報は整理をしよう|ヒトのもつチカラ、「書く」チカラ





















