星田さんの記事に対するコメント。

「アタリマエ」さんを見る。「複素数平面」ってのはよく聞くけど虚数部iは例えると(実部の増減を東北座標の動きだとすると)南北の座標を表すものなのだという。座標を表すのに(x y)とかってしなくても1つの式で表せるのが便利だと、確かに!プログラミングの場合を考えると取り扱いがメチャクチャ楽になりそう(使えるのかまだ知らんけどね)
SchemeやRacketも当然複素数は扱える。殆どのLisp系言語には死角がない、のだ。
と言うか、数学的に扱う「数」に対しては、偶然にも日本での高校数学程度のブツはビルトインで完備してる、ってのが多くのLisp系言語の特徴。
分数を始めとして複素数まで扱える、と言うのは、基本的な数値計算に於いても、Lisp系言語はほぼ無敵だ、と言う事だ。ハッキリ言うとC言語なんかよりも単純な数値計算は得意だ。
ただ、何故にLispが「遅い」と思われてるのかの秘密もここにある。LispはC言語的なナイーブな数値を結果扱わない。「至極複雑なデータ型を内包している」んだ。結果、データ処理が足かせになって速度が稼げない可能性があるわけ。
次の例を見てみよう。

Scheme/Racketでは上の数式は次のようにして記述する。
> (* 1+i 0+i)
-1+1i
> (* 4+2i 0+i)
-2+4i
>
Lisp的にはビックリするだろうが、Scheme/Racketでは複素数は実数部+虚数部iと記述する。そして重要なのはこれらは合わせて1個の数である、と言う事だ。れっきとした数値データだ。関数等ではない。
言い換えると0+iあるいは0+1iと言うのが虚数単位と言う事になる。ここをまず押さえておこう。
座標にiを掛けると(確かに)グラフ上で90度左回転するな・・今回関係があるか知らんけどプログラミングだと画像の回転とかに使ったりするのかな?基本、そんだけの解説だった。
発想がいい。
ただし、複素数を取り上げる前にまずはオーソドックスな「回転」を覚えよう。

まずは星田さんのアバターアイコンを使って、初期状況が次のようなウィンドウになるプログラムを組む。

まず、このウィンドウは480x480と言うサイズを想定している。これは星田さんのアバターアイコンの画像サイズが240x240と言う事から導いたサイズだ。
星田さんの写真を4つ配置するのは次のコードでplace-imagesを用いた事に拠る。
(define (place-hoshida w)
(place-images (make-list 4 *hoshida*)
`(,(world-posn1 w) ,(world-posn2 w) ,(world-posn3 w) ,(world-posn4 w))
*background*))
place-imagesの第一引数で大域変数の星田さんの写真から4つの要素を生成したリストを使っている。
また、今回のworld構造体は4要素だが、どれも座標を表すposn構造体になってる、ってのが前提だ。4枚の写真を4つの座標と関連付けたい、ってのが意図だ。
さて、座標を「回転」させるには通常、昔の高校数学(数II?)で扱った回転行列と言うものを用いる。

さて、三角関数が出てきたね(笑)。ここでθは角度でプログラム上では単位時間毎に変化していく数値って事にしてるんだけど、その辺は後回しにしよう。
いずれにせよ、この回転行列を任意の座標(数学上では原点からのベクトルと言うが)を掛けると座標が「回転」する。
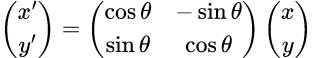
x'とy'が回転後の座標だ。
行列の計算方法を覚えてるかどうかは分かんないけど、計算過程はこうなる。

ベクトルa = (x, y)とベクトルb = (i, j)があって、xi + yjと言う計算を行う事を内積を取ると言う(※1)。つまり、行列とベクトルの「掛け算」と言うのは事実上、行列の行(横の並び)をベクトルと見なして、(x, y)との内積を行数分だけ作っていく事に他ならない。それも「何で?」じゃなくって、単なる定義だ。計算の約束事だ。よって単純に従おう。
僕らみたいな応用数学の立場だと、数学理論が云々、と言う話より結論が欲しいんだ。長ったらしい理論的な話を理解するよりも、与えられた数式がプログラム可能なものなのか、そして実際に使えるものなのか、の方が重要だ。
数学教育的な立場から言えば「こらこら」と言うような発言になるが(笑)、実際その通りなんだ。こういう応用数学的な立ち位置、ってのは何もプログラミングに限らず、物理学なんかでも似たようなモノだ。数学は道具であって、応用数学的にはひと握りの理論屋を除けばそんなに深くは立ち入らないわけだ。
例えば上で挙げた内積とか、どうしてそんな計算を定義したのか理由を考えるよりプログラミング出来るか否か、の方が重要だろう。そしてユーティリティとして考えた時、使い回せるか否かの方が重要だ。
;; 内積の定義例(define (dot-product vec0 vec1)
(apply + (map * vec0 vec1)))
そしてもっと言っちゃうと数式を「読む」よりプログラムを「読む」方がラクになっちゃえば幸いだ(笑)。
回転行列にせよ、ここではθ(theta)がどんな値なのかは不問とするが、プログラムで「書ける」か否か、が重要になる。
;; 回転行列の実装例;; リストのリストにすればいい。(define *rotate-matrix*
`((,(cos theta) ,((compose - sin) theta))
(,(sin theta) ,(cos theta))))
回転、もやっぱりプログラムが書けるか否か、がポイントになる。
;; 回転の計算を行う関数の例
(define (rotate vec)
(map (lambda (x)
(dot-product x vec)) *rotate-matrix*))
これでベクトルの原点周りの回転は記述出来た。
ただし、最初に提示したプログラムがちとややこしいのは、原点周りの回転じゃない辺りだ。
グラフィカルなプログラムにしばしば起こるんだけど、通常、座標(0, 0)と言う原点はモニタの左上隅とかウィンドウの左上隅になる。
一方、先程設定した星田さんのアバターアイコンのサイズから作ったウィンドウは480x480だった。つまり、ウィンドウの中心は(240, 240)と言う座標になる。
そして、星田さんの4枚の座標を(240, 240)を中心として回転させたい。
こういう場合、回転行列を用いた計算は次の式で表される。

a, bは中心とする座標ベクトルの要素だ。今はaもbも240になる、と言う事が分かる。
そして上記の式を書き換えると次のようになる事が分かるだろう。
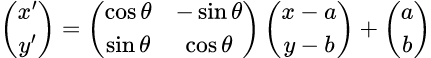
要は、
- 与えられた座標(あるいは座標群の中心)を原点に移動させて、回転させた後、移動させた分だけ元に戻せ
と言ってるわけだ。
それをバカ正直に実装したのがplace-hoshida-on-tick関数になる。
(define (place-hoshida-on-tick w)
(let ((matrix `((,(cos 1/28) ,((compose - sin) 1/28)) ;; 回転行列
(,(sin 1/28) ,(cos 1/28))))
(posns `(,(world-posn1 w) ,(world-posn2 w) ,(world-posn3 w),(world-posn4 w))))
(apply world
(map (lambda (k)
(apply make-posn k))
(map (lambda (i)
(let ((x (posn-x i)) (y (posn-y i)))
(map (lambda (j)
(+ (* (car j) (- x 240)) (* (cadr j) (- y 240)) 240))
matrix))) posns)))))
リストをposn構造体に変換し、なおかつ返り値でworld構造体を組み立ててるのでややこしく見えるかもしれないけど、基本的には、上で書いた通り、各画像を(0, 0)周りに配置しなおした後回転、そしてその後、中心(240, 240)周りに戻している。
なお、回転行列のθを1/28にしてるのは、big-bangの時間計測(on-tick)の最小値が28分の1秒だから、だ。動画性能としては28フレーム、って言い方も出来るのかな。
つまり、place-hoshida-on-tickって関数はbig-bangのマクロon-tickに与えて、28分の一秒毎に画像更新情報を送る。具体的にはworld構造体に含まれる位置情報を28分の一秒毎に更新する。
(big-bang (world (make-posn 360 240) ;; 座標初期値
(make-posn 240 360)
(make-posn 120 240)
(make-posn 240 120))
(on-tick place-hoshida-on-tick) ;; ここで単位時間毎に座標データを更新する
(to-draw place-hoshida))
そうすれば、ウィンドウの中心周りで星田さんの画像がくるくる回るわけだ。

とまぁ、これが「回転」の基本だ。非常にオーソドックスな手だ。
なお、何回か言った事があるけど、この「行列演算」ってのが実はコンピュータが大の苦手で、その計算に特化したGPUが1990年代のプレステ1辺りからポピュラーになってきた。今のPCに含まれてるGPUもこの行列演算が重要な機能になっている。
さて、「回転」の基礎を押さえておいて。
次は果たして、「回転行列」の代わりに複素数を用いても回転が表現出来るかどうか考えよう。
平たく言うと、複素平面上で座標を表す複素数に別の複素数を掛けると「座標が移動する」と言うのがポイントになる。
じゃあ、その「掛ける複素数」をどうするのか。今回は「回転」がテーマなんで、角度を含む複素数、そう、件の有名なオイラーの公式を使ってみよう。
オイラーの公式を再録する。
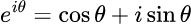
まずは手始めにオイラーの公式の右辺を使用しよう。
これをLispでプログラムするには、取り敢えずθを保留しておくと次のように書ける。
(+ (cos theta) (* 0+i (sin theta)))
繰り返すが、Scheme/Racket上では0+iが虚数単位となる。
そして上の回転行列のプログラムでもそうだったが、複素数同士でも「回転」は原則原点周り、となる。つまり、やっぱり座標の移動が必要になる。
そこで、座標を引いたり足したりする際、ウィンドウの中心部も複素数で表現したい。その値は当然、
240+240i
になる。
この2つの前提でplace-hoshida-on-tickを複素数で書き直すと次のようになる。
(define (place-hoshida-on-tick w)
(let ((r (+ (cos 1/28) (* 0+i (sin 1/28))))
(posns `(,(world-posn1 w) ,(world-posn2 w) ,(world-posn3 w) ,(world-posn4 w)))
(convert 240+240i)) ; 原点とウィンドウの中心の座標変換に使う
(let ((z (map (lambda (i)
(+ (* r (- (+ (posn-x i) (* 0+i (posn-y i))) convert)) convert))
posns)))
(apply world
(map (lambda (x)
(make-posn (real-part x) (imag-part x))) z)))))
元々、ウィンドウの座標情報は実数x, yの組だった。それらから単一の複素数を作らなきゃならない、つまり複素数への変換が必要にせよ、確かに回転行列よりも関数自体はシンプルに書けるんだ。これは大きい。
気をつけなければならないのは、Schemeの複素数から実数部を取り出すreal-part関数と虚数部を取り出すimag-part関数を使って、またposn構造体を作った上でworld構造体を生成して返さなければならない。しかし「データ変換が要り様」だとしても回転行列版よりも遥かにシンプルになっている。
言い換えれば、複素数で平面を表現するのは、確かに記述上超強力なんだ。
次はオイラーの公式の左辺を考えよう。オイラーの公式は等式なんで、左辺と右辺は同じ量を表す。言い換えれば回転するのに三角関数の力を借りなくてもいいと言う事だ。
オイラーの公式の左辺はScheme/Racketでは
(exp (* 0+i theta))
と表現出来る。関数expは自然対数の底(ネイピア数)のn乗を返してくれる。そして乗数は虚数でも構わない。Scheme/Racketはそんなまさしく数学チックな計算指定でもヘーキで処理してくれるんだ。Lispってサイコーだろ(笑)?
右辺版で三角関数を使って複素数を作り上げたトコに上の式をハメ込めば「3つ目の回転方式」を試す事が出来る。
(define (place-hoshida-on-tick w)
(let ((r (exp (* 0+i 1/28))) ; ここを変更
(posns `(,(world-posn1 w) ,(world-posn2 w) ,(world-posn3 w) ,(world-posn4 w)))
(convert 240+240i))
(let ((z (map (lambda (i)
(+ (* r (- (+ (posn-x i) (* 0+i (posn-y i))) convert)) convert))
posns)))
(apply world
(map (lambda (x)
(make-posn (real-part x) (imag-part x))) z)))))
と言うわけでオーソドックスな回転行列を利用した「回転」からはじまって、オイラーの公式と複素数座標を用いた回転2つを紹介した。
シチュエーションによって使い分ければいいと思う。少なくとも武器が3つある、と言う事は悪くはないだろう。

複素数で回る女のケツ(謎
※1: 内積がある、って事は当然外積もある。












