ぼちぼちゆるゆる その２

書きかけたデータの話。
1000シリーズ9000問に触れましたが、一つのマトリクスに1ずつを加えて、
１のマスは２に、２は３に、・・・9は１に書き換えて新しいマトリクスを
作り出します。1つの親マトリクスから8つの子マトリクスができるので、
9個をひとまとめにして、1シリーズと呼ぶことにします。
また、1問につき、回転、反転、それらの組み合わせにより、
7つの位相系の派生形が生じます。さらにそれぞれの不等号の向きを
すべて反転させた補数系の派生形も登録しました。
これら16問は見た目は違っても基本のDNAが同じなので
ひとまとめにして、ファミリーと呼びます。
階層的には、9×9の数字の集団をマトリクス、
同じDNAで出来ている派生形15個を加えてファミリー、
1を加える変形（親戚ってことかな）が９つ集まってシリーズとなります。

え、問題発生？・・・・。


fig.1は明らかに複数解なので採用はしないのですが、
20分以上かけて解いたfig.2はどうでしょう。
＋1の変形を加えたfig.2aでは、複数解が発生しているので
fig.2には規格外の烙印が押されることになります。
親マトリクスだけ複数解がないパターンを「一喜八憂」と呼ぶとか呼ばないとか。
こんなことが度々あったので、家元の問題作成ソフトには
やがて複数解予備審査ルーチンが実装されました。
以降遠回りしていた無駄がかなり省けたと思います。
こんな難し目のfig.2なんかはお蔵入りにするにはちょっと口悔しいので、
データを管理するExcel のbook に、scrap というsheet をこしらえて
苦闘の痕跡を残しておいたのが、ちりも積もって宝の山に見えてきた。
規格外のマトリクスも有効に使える不等号データの数値化に
繋がっていきます。（結果的に重複の発覚にも繋がっている）。
プログラムのサイズを圧縮するために発案したシリーズ化を放棄して、
そもそも9×9のマトリクス・データを内在させておいて、
実行時に読み出すやり方をやめて、144個の不等号の向きを
数字に置き換えたデータからマトリクスを復元することにしました。
1列の不等号は最大2種類8個。0と1に置き換えれば2進8桁。
さらに書き換えれば見慣れた16進2桁。
これが縦横合計18個あれば復元できる理屈。
ただし難題が持ち上がる。答え合わせが難しい。
9×9のマトリクス・データを基にことを進めた場合は、
（ A 、B )のマスに N が配置されたか、という判断を
81のマスに対して行えばよかったから、
正解、そうでない場合はこことここがミスですよと明示できた。
ところが数値化した不等号でのゲームの場合、144か所の大小関係がすべて
成立していれば正解と断定できるものの、不正解の場合にはどの不等号が
成立していないかは明示できても、このマスはミスと断定できない。
例えば上に示したfig.2。７と8を全て入れ替えて回答したとする時、
成立していない不等号は、７と8が直接隣り合っている、
上から5段目と8段目の2ヶ所だけになります。
このあたりのもやもや感とは上手に付き合っていただくことにして
家元は Excel の関数とマクロを駆使してデータベースづくり。

不等号の向きで0と1に書き分ける if 関数、そのデータが入った
セル情報をくっつけちゃう concatenate 関数、
その結果できた4桁の2進数を16進数に変換する bin2hex 関数、
そのセルを2つくっつけて・・・、と関数たちが八面六臂の大活躍。
マクロもデータが大きくなればなるほど威力を発揮する。
上の説明図のように、右隣に1を加えた子マトリクスを書け、
それを8回繰り返せ、ということがマクロの書き方次第で可能だ。
不等号の向きの数値化データ作成には、
sheet A のマトリクスをsheet B にコピペし、
16個の演算結果をsheet C にコピペしろ。
ペーストした最終行の次の行のセルを次にペーストするセルだと
覚えておけ、
sheet A に戻れ、
さっきの起点のセルから10行下のセルを次の起点だと覚えろ、
今のマクロを71回繰り返せ
というマクロがフル回転。
7回ボタンを押すだけで500ファミリーのうち
497ファミリーの処理が終わってしまう。残りの3ファミリーは
基本のマクロを3回やればいいってわけ。

2008年の前のブログ立ち上げ時点で、500シリーズ4500問の
ストックがありました。ただ難易度の分布に偏りがあって、

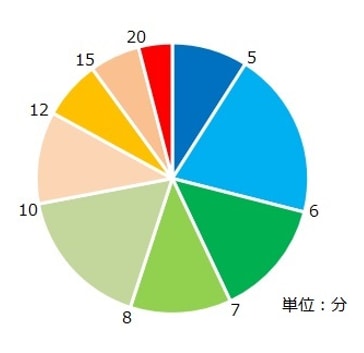
こんな風に簡単に解けてしまう問題の割合が結構大きかったので、
不等号ナンプレが軽く見られがちな風潮を打破すべく、
エディタを積極的に使って、難しそうな問題作りを始めたのが15年初夏。
後期型500シリーズ4500問揃えるのに、2年半かかりました。
ナンプレ配列が何通りあるか試算したら10の22乗という天文学でも
扱わないような答えが出たので、ダブルブッキングのチェックは
必要ないと考えました。もう一つのチェックをやめた理由が
Excel で扱えるデータ数が１列あたり65535行までということで、
9000×16＝144,000個のデータは一度には扱えない、
というのもあったかな。
4500問のマトリクスデータ内在型の不等号ナンプレのゲームは
前期型と後期型の2つあったわけだけど、
不等号の向きの数値化データ提供型だと、重複さえしていなければ
一つの大きな集合として扱うことが可能となるし、
一喜八憂タイプの復権も見えてくる。
あれとこれは同じじゃないかとクレームが入らないようにと
16進で表示する不等号データの最初の1文字ごとに調べてみたら
見つかったんです、12シリーズ。で、その穴埋めのために108問、
解きまくりました、なんでこんなことをやってるんだろうって
思いながら、所要時間の平均が12分オーバーのちょっとキツいのを。
おかげで、難易度の水準は落とさずに済んだようです。

また折を見て近況とやらを書いてみます、まずはここまで

ぼちぼち ゆるゆる 不等号ナンプレ宣伝隊活動再開

え、開設の意気込みですか？
まあ、ぼちぼちゆるゆるっていうことで、マイペースでやります。
以前のブログを、「突然ですが」って中断してもう9年。
世の中を見回してみると、ニュースタンダードとかいうひとくくりで
すっかり変わっちまったものもあれば、相変わらずのものも。
4年余りで3000問を超える不等号ナンプレを公開した
以前のブログのほうは、「不等号ナンプレ」と画像検索してみると
それらしいのは残っているが、記事のほうは長期間の放置で、
検索のランキングがずーっと下位になったみたいで到達困難かも。
日曜恒例の難問用のツールもリンクが途切れて利用不可。
私はというと、相変わらず、ヒントの数字の入っていない不等号ナンプレを、
我が世の春の来ることを信じながら、育てております。
今、企てているのは、ナンプレの問題を打ち込んで、
解くのをサポートするプグラム。ってのはあるんだろうから、
解き終えたら、不等号ナンプレの複数解をチェックして（ここは手動）、
無さそうだったら、不等号ナンプレとしての愉しみを満喫する、
というプログラム。ナンプレ解きは、絞込みを強力にアシストしてくれるので
はかどるはかどる。目標30分という問題が1分で解けたりしてる。で、
次は不等号ナンプレ。複数解をチェックするんだけど、実はこの1年で
ナンプレを2000問ぐらい解いてるのね、自作ソフトを使って。
で、何がわかったかというと、どの問題集でも複数解になってしまう割合が
7割で、ほとんど差が出ないということ。で、残った3割を解いてみて、
所要時間を記録するなんてことを、ほめられもせず　苦にもされず
やってたんですよ。
それから、企てその２。1問あたり144個ある不等号の向きを数値化した
16進6桁×6個のデータを提供し、それを入力して、マトリクスを再現してもらい、
不等号ナンプレを解いてもらうというプログラム。
プログラミングと並行して提供するデータを作ってたら、
1000シリーズ9000問の中に重複が12シリーズも見つかった。
問題作成時に出自を書き留めていたから、1媒体から2度採用することは
考えにくい。とすると一つのマトリクスを2つの媒体が出版したのを
それぞれ採用しちゃったのかな。ま、同じマトリクスでも
片方は数字が32個入っている初級問題、もう片方は数字が23個の
上級問題だったということは考えられなくもない。
ともあれ、重複分、12シリーズ108問を補充しました。とさ。
あ、データについて説明しておいたほうがいいかも。
でも長くなりそうだから、日を改めることにして、まずはこれまで。