悪いネタもない。
なので今日はネタなしということで。
----
体重:80.8kg 体脂肪率:26.6% 脂肪量:21.5kg 筋肉量:56.2kg
----
ネタもなければコメントもない。おわり。
昼食という名のカップ麺のストックが切れたので近くのドラッグストアで買ってきました。
量の割には価格が安くコスパがいいのでお気に入りです。
ついでに大学ノートを2冊ほど買いました。
文章を書く依頼を受けたので下書きとして使おうかな、と。
え？Word？テキストエディタ？スマホ？残念ながら下っ端なのでパソコン類には触らせてもらえず。スマホも印刷ができないので除外。
しかもテレワーク未導入で職場で依頼をこなさないといけないので結局大学ノートを使うことに落ち着きました。amazon？届いてからじゃ遅い！
話はかなり変わって、ダイエットの話。
すり足ウォーキングをしていたら絨毯の状態に違和感を覚えました。
どうやらすり足し過ぎて絨毯の毛がそこだけペッタンコになっていたようで。
おまけに畳の上に敷いていたので畳のフチのラインがくっきりと。
でも絨毯のおかげか畳が傷んでいるわけではないので、すり足ウォーキングは続けます。
----
体重:82.3kg 体脂肪率:28.3% 脂肪量:23.3kg 筋肉量:56.0kg
----
わはははは！ こりゃまた けっさくだべ！
……と言いたくなるような値の変わりよう。一時的なものだと信じたい。
自分がまとめたイラストロジックの解答講座がGoogle先生にどんな扱いをされているか、いわゆるエゴサーチなるものをしてみました。
1ページ目に出てきたのですが、そこはgoo blogの検索結果。
そこからさらに調べてみると……イラストロジックについての記事は今年に入ってから自分しか書いていないことがわかりました。
というより、イラストロジックというジャンルの記事自体かなりマイナー。開拓する以前の問題。
Google先生からも先駆者のイラストロジック解答講座を検索結果の上の方に出される始末。
なんだかモチベーションががくっと下がったみたいなので、解答講座は一旦中断します。
コメントや解答講座記事の評価次第では再開するかもしれません。
……エターなるとはよく言ったものですが、ツクールで何度も経験しているとはいえブログでも経験することになるとは。
まあ、ダイエットや自動解答ツールの製作に時間を回せるだけマシでしょう。タブンネ。
----
体重:82.6kg 体脂肪率:26.4% 脂肪量:21.8kg 筋肉量:57.6kg
----
筋トレと有酸素運動を行うなら筋トレを先にやってから有酸素運動をするといいというのがGoogle先生のアドバイスらしいですが、最近は運動をあまりしてなくても測定結果がまあまあいい感じになっているのですが。
この状態で運動を再開したらもっと測定結果が良くなるんでしょうかね？
とりあえずすり足ウォーキングを毎日30分以上を目標にしてみますか。
せっかくウォークマンがあるんですし。
誰かの役に立つと信じて一生懸命努力しても、誰も応援してくれない。
資料を用意して、発表しても誰にも聞いてもらえない。
ああ、むなしい。
今はそんな気持ちです。
でも、現実では努力するのは自由でも価値がなければ発表の場は与えられないんですよね。
発表の場が無条件に与えられているだけでも幸福だと考えるのが当然なのでしょう。
でも、むなしい。
----
体重:82.2kg 体脂肪率:26.8% 脂肪量:22.0kg 筋肉量:57.0kg
----
＊むなしい きじの かずかずが せすじを つたう。
今回は「全く手を付けていない解き始めの状態」から「確実に塗れるマス・塗ってはいけないマス」を導く方法のPart3です。
今回はヒント数字が「2つ以上」の場合について考えます。
今回は電卓があるとやりやすいかもしれません。
さて、ヒント数字が「2つ以上」の場合の例を挙げてみます。今回は「6 3 2」幅「15マス」とします。
とりあえず「6」「3」「2」の順で成立する全てのパターンを洗い出してみます。
「6」は緑、「3」は赤、「2」は水色で色分けしました。わかりやすさという理由もありますが、他にも理由があります。それは後述。
全部で10パターンとなりました。多いですね。
さて、これを縦に見て白マスにならないマスをあぶり出してみます。すると、
こうなります。水色の「2」は最初の1パターンだけ白マスになるマスがあったので全部消えてしまいました。
この残った5マスは白マスになるパターンがないので、「確実に塗れるマス」となります。よって、
この例はこの形で一旦落ち着きます。
ところで、今回の例は10パターンで済みましたが、毎回総当たりしていると時間がいくらあっても足りませんし、そもそもそんな時間は無駄です。
そこで役に立つ考え方が「両端寄せ」の考え方です。
簡単に言うと、「塗れるマスの塊を限界まで左端・右端に寄せた状態だけを考える」考え方です。
上記の完成形も添えて2パターンに絞ってみます。
最初の10パターンから、一番上と一番下のパターンだけを抽出しました。
これだけでも「同じ色の」マスが確実に塗れるマスと一致していることがわかります。
しかし、これだけだと1つ問題点が浮かび上がってきます。
ピンクのマスはこの2パターンだけを考えた時に白マスになっていないですね。
しかし、実際はそこは未確定のマスです。
この問題点のポイントはただ1つ、「異なるヒント数字に対応したマスが重なっている」ことです。
この「両端寄せ」の考え方では、「同じヒント数字に対応したマスが重なるマス」だけが「確実に塗れるマス」となることを忘れないでください。
なお、「同じヒント数字」とはいっても「同じ値のヒント数字」ではありません。順番が異なればそれは「異なるヒント数字」となります。
例として、「5 5 1」幅「15マス」を考えてみます。
ピンクのマスはそれぞれ「緑の5」と「赤の5」、「赤の5」と「水色の1」と重なっていますが、やはり未確定のマスです。メモ帳なりペイントソフトなりで試してみるとわかると思います。
さて、この「両端寄せ」の考え方ですが、いちいち紙か何かに書き起こしていたら時間も紙も余計に消費してしまうでしょう。
そこで朗報、この「両端寄せ」を暗算する「公式」が存在します。いよいよロジックパズルらしくなってきましたが、実はここがイラストロジックで一番つまづきやすいポイントだったりします。
その公式とは、「列の幅－ヒント数字a－ヒント数字b－ヒント数字c－……－ヒント数字n－ヒント数字の個数＋1」です。はい、ややこしいですね。
では、先に挙げた例2つを公式に当てはめてみましょう。
ヒント「6 3 2」幅「15マス」の場合：「15－6－3－2－3＋1」＝「2」
ヒント「5 5 1」幅「15マス」の場合：「15－5－5－1－3＋1」＝「2」
偶然にも同じ結果になりましたが、それは置いといて……。
さて、この公式の値、何になるのか？それは、「公式の値より大きいヒント数字は確実に塗れるマスが存在する」ということがわかることです。
公式の値をヒント数字から引き算して、「1以上」になればそのヒント数字は「確実に塗れるマスが存在する」ことになります。
ヒント「6 3 2」－「2」＝「4 1 0」
ヒント「5 5 1」－「2」＝「3 3 -1」
これで1つ目の例は「6」と「3」、2つ目の例は「5」と「5」に確実に塗れるマスが存在することがわかりました。
では、ここからどうやって「フィールドに出力」するのか？
そのコツは、「1、2、3、4、……とカウントアップしながら、公式の値より大きい値になったらそこを塗る、ヒント数字と同じ値の次は『トン』と、一拍置いてまた1、2、3、4、……と繰り返していく」ことです。
サンプルとして2つの例を左と右の両方からカウントアップした画像を用意しておきます。
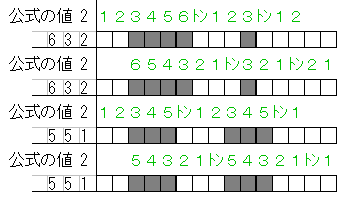
公式の値「2」より大きい「3～」の下のマスが確定マスとなっているのがわかると思います。
これをマスターすれば第1の壁は越えたも同然です。
なお、電卓があるとやりやすいと書いたのはこの公式の値を暗算ではなく電卓で導くことができるからです。
特にジャンボロジックになると暗算だと厳しくなってくるので、電卓でも導けるようになると便利です。
ヒント数字と個数を「引き算」して最後に「1足す」というのがややこしいですが、これができるとできないとでは天地の差があるので確実にマスターしたいところです。
ちなみに公式の値が「0」になったらその列は確定します。前述のコツにならえば、「トン」の部分は×マス、他のマスは確実に塗れるマスになります。
また、この公式はヒント数字が1つの場合でも成立します。ヒント数字が「0」でも一応成立しますが、その列は無条件で全部×マスになるので特に意味はありませんが。
長くなりましたが、今回はここまで。次回からは「すでに確定したマスがある状態」から発展させる考え方について取り上げます。