知識の木の実

知識の木

　アダムとイヴの伝説によれば、人間が最初の統一を去るようになった誘惑は蛇によって人間にやってきたことになっています。

　しかし実際は、「対立」へ足をふみ入れること、すなわち意識の目覚めは人間自身のうちにあるのであって、このことは、あらゆる人のうちで繰り返されている歴史なのです。

　　ヘーゲル｢小論理学§２４

　ランベール画｢善悪の樹」

　　

　

　生命と知識

　わたしたちは知識を得るために分析・分解します。わたしたちは知覚のうちに、多くの要素からなる具体的なものを持っています。

　知識を得るためわたしたちはそれらの緒要素を、まるで玉ねぎの皮でもはぐように分解するのです。そして分解ということ以外には何もつけ加えないと考えています。

　しかし実際には「知覚」を「思想」に変えているのです。具体的なものを抽象的なものに変えているのです。

　もし具体的なもの、統一的なもののみが「生命あるもの」なら、このような方法は同時に生命あるものを殺していることになるのです。　

　　　　　　　　同§３８

　多くの人は、認識するということは与えられた具体的な対象を抽象的な要素に分解し、これらを個々別々に観察する以外なにもすることができないと言う。

　しかし、こうした方法が事物を変化させるものであり、あるがままに事物をつかもうとする認識は、そのさい自己矛盾におちいることはすぐわかります。

　たとえば、化学者は一片の肉をレトルトに入れて、それをさまざまな方法で処理し、それが窒素、炭素、水素などから成っていることがわかったと言います。

　しかし、これら抽象的な素材はもはや決して肉ではないのです。経験的心理学者がある行為を観察し、そこにおいて示されるさまざまな側面を分解して、これらをあくまで分離する場合も同じです。分析の対象は、いわば、人がその皮を一枚一枚はいでいくタマネギのように取り扱われているのです。

　　　　　　　　　同 § 227

　たとえば、生きた肉体の肢体や器官は、単に部分とのみみるべきものではありません。なぜならそれらは、それらの統一のうちにおいてのみ、肢体や器官であって、決して統一に無関係なものではないからです。それらは、解剖学者の手にかかるとき、はじめて単なる諸部分となるのであり、解剖学者が取り扱うのは、もはや生きた肉体ではなくて、死体にすぎないのです。　　同§136

　肉体の個々の分肢はその統一によってのみ、また統一との関係においてのみ、それらがあるところのものであります。たとえば、身体から切り離された手は、すでにアリストテレスも言っているように、名の上でのみ手であるにすぎず、事実においてはそうでありません。　　同§216

ランベール画｢善悪の樹」

　知識の木の実

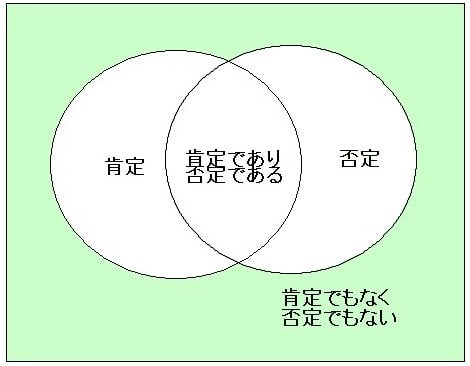
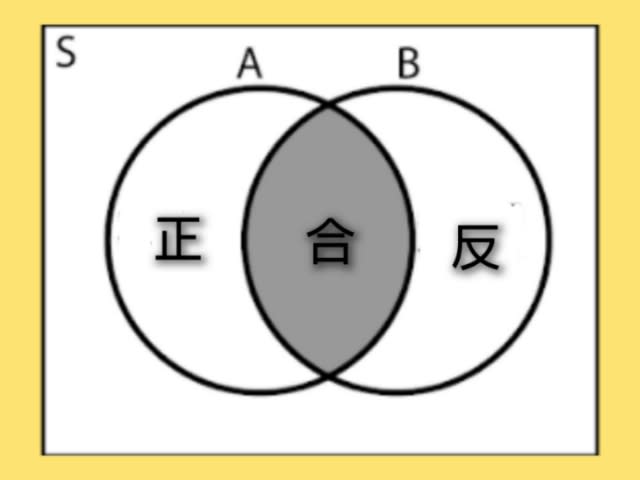
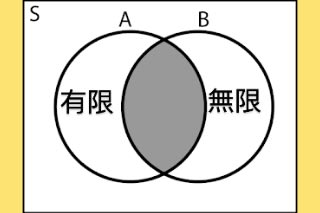
　わたしたちが知識の木の実を食べるとき、すなわち反省により意識が知識へと変わるとき、現実であったものが観念的となり、具体的であったものが抽象的になり「一」であったものが「多」となります。

　ここにおいて一方に神あれば一方に世界あり、一方に我あれば一方に物あり、すべての物は互いに相対し、すべての物は対立するようになるのです。

西田幾多郎「善の研究」四篇四章より

西田 幾多郎（にしだ きたろう、1870 - 1945は、日本の哲学者。著書に『善の研究』などがある。

弁証法

　弁証法は以下のように説明されています。

弁証法

　物の考え方の一つの型。形式論理学が、「ＡはＡである」という同一律を基本に置き、「ＡでありかつＡでない」という矛盾が起こればそれは偽だとするのに対し、矛盾を偽だとは決めつけず、物の対立・矛盾を通して、その統一により一層高い境地に進むという、運動・発展の姿において考える見方。(不明)

上図は一般的な説明に使われる図。下図は上からの下降図。これを見ると弁証法はいわゆる「ツリー構造」になっているのがわかります。

別の説明もあります。

　

　一つの物事を対立した二つの規定の統一としてとらえる方法。

(日本大百科全書(ニッポニカ)「弁証法」の解説)

対立と統一のイメージ

以下はヘーゲル本人の説明です。

対立するものの相互関係

　常識的には、区別されたものは相互に無関係であると考えられています。たとえば、わたしたちは人間であり、私の周囲には空気や水があり、動物やさまざな物がある、と言う。ここではすべてのものが別々になっています。

　哲学の目的はこれに反して、このような無関係を排してさまざまな事柄の必然性を認識することにあり、他者をそれ固有の他者に対立するものとみることにあります。

　たとえば無機物を単に有機物とは別なものとみるべきではなく、有機物に必然的な他者と見なければならないのです。両者は本質的な相互関係のうちにあり、その一方は、それが他方を自分から排除し、しかもまさにそのことによって他方に関係するかぎりにおいてのみ存在するのです。

　同じように自然もまた精神なしには存在せず、精神は自然なしには存在しないのです。

　　　ヘーゲル　小論理学§119

　主観と客観の同一性が主題になっていますが、ヘーゲルの「小論理学」は仏教で説かれる縁起や不二法門に近いものがあります。その原理自体は簡単なものであるとヘーゲルは言います。

抽象的同一と具体的同一

　真正の宗教あるいは知的直観は、ある人にはとても理解し難いものと、またある人には正真正銘の真理と、また別な人には迷信に類するものと見なされています。

　しかし真正の宗教の主張が神秘的に思えるのは知性に対してだけなのです。しかもその理由は、実に単純なことです。知性の原理が「抽象的な同一」であるのに対し、真正の宗教、または知的直観の原理は「具体的な同一」であること、これだけのことです。

　

　ヘーゲル小論理学§82の意訳

　　

ヘーゲル（1770年 - 1831年）は、ドイツの哲学者。

　

ベン図とオイラー図

オイラー図やベン図は、集合の相互関係を表す図。 オイラー図はベン図とは異なり、各集合を表す円が必ずしも重なっている必要はない。（wiki)

スーパーポジションとは集合Aと集合Bの重なり合う部分をいいます。下図の場合は「Aであり、かつBである」の部分です。

数学ならプラスマイナス０の部分ですが、０の考え方が数学とは違います。

スーパーポジションは重なり合いと状態の共存の場所ですからプラスもマイナスも０もそのまま保存されます。そして赤い部分をみると上図がそのまま繰り込まれています。部分の中に全体が入り、全体がそのまま部分をあらわした構造になっています。論理自体が入れ子構造になっていてこれが無限に続いていきます。鏡の中に鏡が写り、それがまた鏡に写り、それが延々と重なり合う状態です。フラクタル状態とは静止した状態ではなく、時間軸に沿った一種の動きであり、変化でもあります。

ここの０は数式のプラスマイナス０ではなく座標軸の原点のようなものです。プラスとマイナスはあるがその場ではどちらとも区別がつかない、あるいはどちらにでも変化できる状態、といった意味です。

　これは色々な考え方に応用がききます。「重ね合わせと状態の共存」は論理学的に言えば弁証法運動をおこなっているからです。

✽ベン図が便利なので使っていますが、考え方は下図のU磁石からの発想です。U磁石を真上から見たイメージがベン図で横から見たイメージが弁証法です。＋と−は電子のイメージです。弁証法というのは重なり合う部分にプラスとマイナスの二項対立の両項がアウフヘーベン（統一かつ保存され）てゼロという概念になっているからです。

　ですから重なり合う部分は+-がそのまま「ある」という保存状態と、引力・斥力が「ない」という統一状態の二面性をもっているわけです。ここでは「ない」というのは「無」ではなく「統一」のことです。

これを言葉で表現するなら、ゼロとは「あり」かつ「ない」ものだと言わざるを得ません。これを形式論理学では「矛盾」と呼びます。

0と1の間の無限

カントール集合

カントール集合は、フラクタルの1種で、閉区間 [0, 1] に属する実数のうち、その三進展開のどの桁にも 1 が含まれないような表示ができるもの全体からなる集合である。1874年にイギリスの数学者ヘンリー・ジョン・スティーヴン・スミス（英語版）により発見され1883年にゲオルク・カントールによって紹介された。

　カントールの三進集合とも呼ばれフラクタル概念の生みの親であるブノワ・マンデルブロは、位相次元が 0 の図形をダスト（塵）と呼び、カントール集合のことはカントール・ダストやカントールのフラクタルダストと呼んでいた。(wiki)

これをもっとわかりやすく視覚化したのがツリー構造です。

複雑に枝分かれするパターン

　数学的な表現はチンプンカンプンですが、要するに直線の中央の線分の1/3を削除し、残った部分の中央の1/3をまた削除する。そしてこの作業を永遠に続ける。すると最後にはほぼ空白ながら、限りなく短い直線が限りなく多く残るということです。

0と1の閉ざされた有限の中に無限が入り込んだのです。

カントール集合最終のイメージ。

コッホ雪片

　1905年、スウェーデンの数学者コッホはカントールの手法を応用して、のちにコッホ曲線と呼ばれる自己相似な図形を考案しました。コッホ曲線はコッホ雪片の一部として紹介されることが多い。コッホ雪片はひとつの三角形から始まり、各辺の中央の1/3を三角形に置き換えるという作業を際限なく繰り返す。その結果、辺が無限に長く、面積が有限という初期の幾何学者を困惑させるような図形ができる。

(創元社　深遠なる「幾何学の世界」より)

辺の長さは無限で面積は有限です。

0と1という有限の中に無限があるというのは矛盾です。また無限の長さの線分に囲まれた有限な図形も矛盾です。ところがこの矛盾の場所というのが「スーパーポジション」すなわち「共存の場所」なのです。

「有限であり、かつ、

無限」ということです。

見出し画

フィラエ島にある古代エジプトの建物の柱頭にはカントール集合に似た模様が付けられている。

木構造／ツリー構造

上図の「半分にする」という分け方がよくわからないので調べたところIT用語の「木構造」に似ていることがわかりました。

木構造 【tree structure】 ツリー構造

木構造とは、データ構造の一つで、一つの要素（ノード）が複数の子要素を持ち、子要素が複数の孫要素を持ち、という具合に階層が深くなるほど枝分かれしていく構造のこと。木が幹から枝、枝から葉に分岐していく様子になぞらえた名称である。

　　　　　　　(IT用語辞典より)

　現実の木は地中の根から上に向かって幹や枝を伸ばし、葉が上方にあるが、木構造を図示する際にはこれとは逆に、根ノードを図の最上部に描き、一段下に子ノード群、その下に孫ノード群、といった具合に下向きに広がるように描くことが多い。家系図の描き方と同じである。

２分木(Binary Tree)

　下の図のような形のデータ構造を２分木という。それぞれの節(○)は、最大2つの枝を持ち、その枝先には、さらに節を持つ。枝を持たない節を葉ともいう。データの整列や探索などに使用される。

再帰的な性質

上図は、二分木の概念図に、赤い枠を加えたものです。

二分木の一部分を囲っていますが、この囲まれた部分だけを観察してみると、その部分もやはり二分木になっていることが分かります。

　このように、木構造はその一部分だけを取り出してみても、やはり木構造の形をしているという特徴があります。ここで、一部分の木のことを部分木と呼びます。

　この概念図の場合、全体としての根の右側にある部分木を囲っていますが、この場合、根に対して右部分木と呼びます。左側にあれば左部分木と呼ばれます。

　もっと大きな木構造であれば、部分木の中にさらに部分木が、その中にさらに部分木があるという構造になります。このように、自分自身の一部が、自分自身と同じ形状をしているような構造は、再帰的な構造と呼ばれます。

二分木 | Programming Place Plus　アルゴリズムとデータ構造編【データ構造】　第７章より

　図形の「フラクタル構造」の説明と情報の「ツリー構造」の説明を比べて読むと、両者が驚くほど似ているのに気がつきます。あるいは同じことをそれぞれの分野での言葉で言っているだけかもしれません。

見出し画　セェフィロトの樹

生命の樹（せいめいのき、英語: Tree of Life）は、旧約聖書の創世記（2章9節以降）にエデンの園の中央に植えられた木。命の木とも訳される。生命の樹の実を食べると、神に等しき永遠の命を得るとされる。

ユダヤ教のカバラではセフィロトの木（英語: Sephirothic tree）とも呼ばれ、宇宙万物を解析する為の象徴図表に位置付けられている。(wiki)