鏡と鏡を合わせた時にあらわれる無限は虚像ですから、無いものが有るように見えているだけです。しかしそのイメージを損なわないまま実際に存在するものがあります。 



上図はコンピューターで描かれたシダの葉。
シダは、自己相似図形の代表例の1つ。すなわち、数学的に生成されたパターンであり、そのパターンは任意に拡大または縮小しても同一の形状が現れる自己相似性を示します。シェルピンスキーの三角形のように、バーンズリーのシダは、コンピューターで数式を繰り返し使用することで、視覚的に美しい図形を構築しています。
モデルとなった本物のシダの葉

フラクタル構造
フラクタル構造とは、「図形のどの部分を取っても、それが全体と同じ構造になっている」ことを意味します。
例えば、下図のように三角図形の一部を切り取ると、全体の三角図形と同じ構造が見られ、更に切り取った図形の一部を見ると、また同じ形になっている・・というものです。
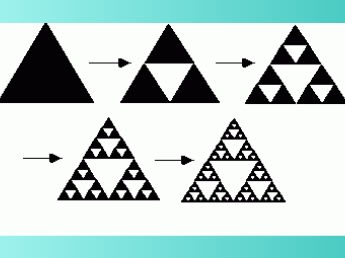
シェルピンスキーの三角形
このようにフラクタル構造は全体の形が、規則的に繰り返されているのが特徴です。
フラクタル構造は自然界の物体にもよく見られ、雪の結晶やブロッコリー、人間の血管などもフラクタル構造と言われています。


自己相似性
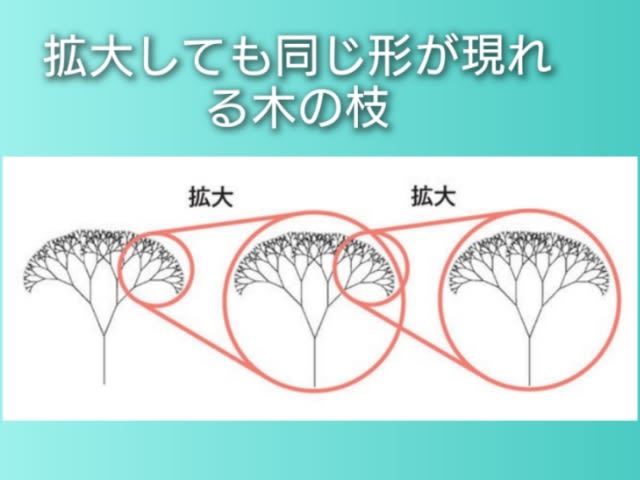
全体と部分とが同じ形をしています。これはフラクタルの特徴で、「自己相似性」といいます。自己相似性とは自分自身のミニチュアがそっくりそのまま自分の中に入っているような構造のことです。


「フラクタル」が無限の正体かもしれません。拡大しても縮小しても同じものが現れます。底もなく天井もなく、どこが始まりかどこが終わりかわかりません。基準になる尺度がないのです。部分の中に全体があり、全体の中に部分があり、切っても切っても同じものが現れます。


見出し画 クリムト「生命の木」