Cube root using abacus: Theory (Triple-root method)

Square root & Cube root

[Japanese]

This is beginning of articles about how to solve Cube root. Today is the theory of Triple-root method. (Sankon method)

Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.

"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.

157,464 -> (157|464): 157 is the 1st group number. The root digits 2.
20,346,417 -> (20|346|417) : 20 is the 1st group number. The root digits is 3.

Cube root of 20,346,417 is 273. We call 1st root=2, 2nd root=7, 3rd root=3.


Case 1) Root is 2-digits

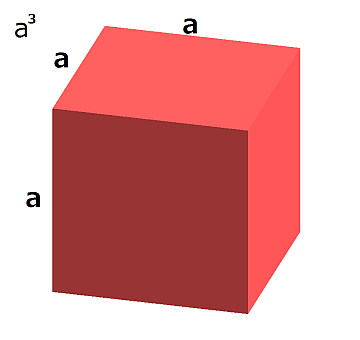
1st root=a, 2nd root=b, then C (Cube) is given by following formula.





Use next formula for the Cube root calculation.








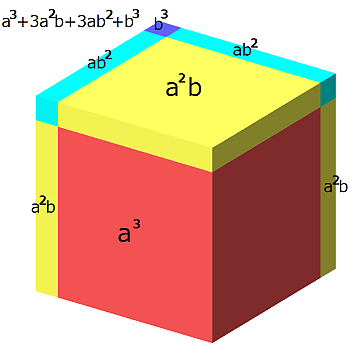
Step 1) Find the 1st root and subtract its cube.

Find the 1st root and subtract its cube from 1st group number.





Step 2) Divide by 3x of the 1st root.

Divide remainder by 3x(1st root). This is why we call the calculation as "Triple-root method".







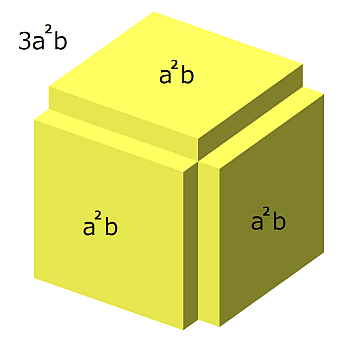
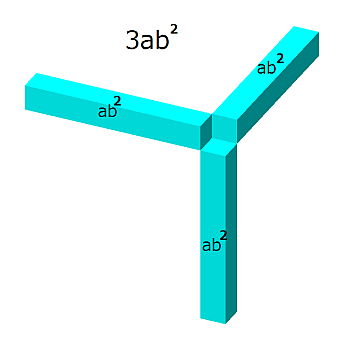
Step 3) Divide by 1st root and get 2nd root.





Step 4) Subtract square of the 2nd root.





Step 5) Subtract cube of the 2nd root.






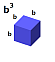
Case 2) Root is 3-digits

1st root=a, 2nd root=b, 3rd root=c, then C (Cube) is given by following formula.









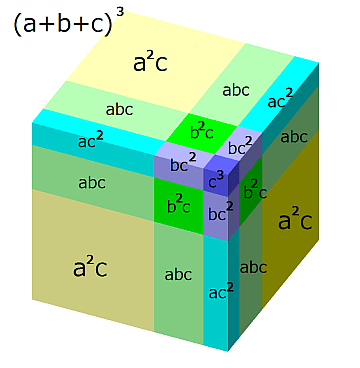
Step 1) Use next formula for the Cube root calculation.





Step 2) Divide by 3x of the current root.



Step 3) Divide by a+b and get c as 3rd root.





Step 4) Subtract square and cube of the 3rd root.






Next article shows how to solve Cube Root by Triple-root method using "Mr. Cube Root" abacus.


Related articles:

How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed

Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b


Please place your mouse on the buttons and click one by one. These are blog ranking sites.