
「ワインバーグの宇宙論(下): ゆらぎの形成と進化」
内容紹介
最新の結果に基づいた宇宙論の教科書。内容の深さ、エレガントさで、他の追随を許さない。 ワインバーグ(ノーベル物理学賞受賞)による、最新の観測結果に基づく宇宙論の教科書。
上巻は、ゆらぎのない、一様宇宙を扱う。下巻では、ゆらぎのある非一様宇宙を扱う。
著者略歴
スティーブン・ワインバーグ: ウィキペディアの紹介記事
1933年、ニューヨーク生まれ。コーネル大学卒業、コロンビア大学でPh.D.を取得。ハーバード大学教授を経て、現在テキサス大学物理学科教授で、天文学科教授も併任。専門は素粒子物理学と宇宙論。1979年に、S.グラショウ、A.サラムとともに電弱理論への貢献でノーベル物理学賞を受賞
翻訳者略歴
小松英一郎
1974年、兵庫県宝塚市生まれ。2001年、東北大学大学院理学研究科博士課程修了。テキサス大学教授を経て、現在、マックスプランク宇宙物理学研究所所長、東京大学高等研究所カブリ数物連携宇宙研究機構上級科学研究員。理学博士。専門は宇宙論
理数系書籍のレビュー記事は本書で257冊目。
上巻を読み始めたのは「宇宙が始まる前には何があったのか?: ローレンス・クラウス」の記事を投稿した6月20日くらいなので、下巻を読み終えるまで2カ月と少しかかったことになる。
途中、日本史の教科書や「宇宙創世はじめの3分間 (ちくま学芸文庫):S. ワインバーグ」を読んでいたので実質は1カ月半くらいかかったのだと思う。読書以外にも「NHK宇宙白熱教室」の感想記事を書いたり、8月ということで第2次世界大戦関連のドキュメンタリー番組をたくさん見ていたし、本業の仕事のほうが超多忙だったので科学系の勉強にあてる時間はいつものペースの半分に落ちていた。忙しいながらも仕事や勉強をしたりテレビを見たりできるのも日本に平和が続いているからだと思うわけである。理屈がどうあろうとも二度と戦争はしてはいけない。戦争に結びつく可能性のある選択は絶対にしてはいけないと思った。
下巻では、ゆらぎのある非一様宇宙を扱う。章立てはこのとおり。
第5章:小さなゆらぎの一般論
第6章:宇宙論的ゆらぎの進化
第7章:マイクロ波で観た空の異方性
第8章:構造の成長
第9章:重力レンズ
第10章:宇宙論的ゆらぎの起源としてのインフレーション
上巻のレビュー記事で僕はワインバーグ博士のことを「コンピュータの計算能力に古典的な解析学の手法で立ち向かう年老いたドン・キホーテのようだ」と表現したが、下巻ではさらに数式の難易度が増す。下巻の主なテーマは宇宙論的なゆらぎであり、場の量子論で使われる数学的手法が駆使されている。すなわち場の量子論は下巻を理解するための大前提となる。もちろん一般相対性理論を理解していることも前提だ。
COBEやWMAPによる観測で明らかになった宇宙マイクロ波背景放射の揺らぎが数式で計算できるのだ。すごいではないか。宇宙誕生の瞬間に生じたゆらぎが宇宙が膨張するにしたがってどのように進化(成長)して現在観測されているサイズのゆらぎになるかということも含めて、博士はすべて本書で計算を示している。たとえ数式が難しくて理解不能であっても、その導出過程を「鑑賞」するだけでも読む価値があると僕には思えた。
宇宙の歴史はその膨張過程においていくつかのフェーズに分けて考えることが必要で、それぞれの段階での温度や宇宙を構成している素粒子について摂動法に基づいた微分方程式をたてるのが第一段階だ。この微分方程式の厳密解は求められないので近似的な解法が必要になる。
博士が用いているのは流体力学(確率の流れ)を導入した近似的な解法である。これに対し通常行われているコンピュータによる解法は統計力学をベースにした連立ボルツマン方程式を数値的に解くものだ。途中の段階でWMAPによる観測によって得られた宇宙論的パラメータをあてはめて、具体的な解を導くのだが、博士が求めた流体力学による解とコンピュータが計算する統計力学的な解、そして観測から直接得られる値は見事に一致する。宇宙論的パラメータのような大域的な量から局所的なゆらぎやその時間の経過による大きさの変化が求められるというのが興味深い。
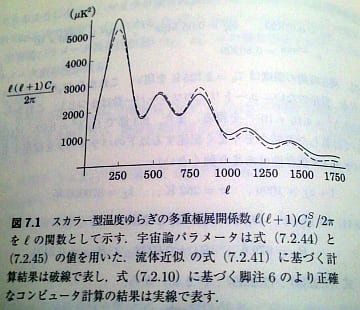
このグラフは「CAMB Webインタフェース」のページのいちばん下の「Go!」ボタンをクリックすると表示されるので、ぜひ試していただきたい。
第5章:小さなゆらぎの一般論
この章では解析に必要な基礎を得るため、小さなゆらぎの進化を記述する一般相対論的方程式を導いた後、ゆらぎに関する一般的な性質を学ぶ。
第6章:宇宙論的ゆらぎの進化
この章では解説の中で導く式を用いて放射優勢期から物質優勢期を経て脱結合の時刻という現在近くまでのゆらぎの進化を調べる。まずスカラー型摂動を記述する方程式を書き下す。これらの方程式は冷たい暗黒物質とバリオンのプラズマに関しては単純な流体力学の方程式となるが、光子とニュートリノに関して高精度の計算をするには位相空間における分布関数の進化を記述する連立ボルツマン方程式を解く必要がある。これらの方程式は複雑すぎて解析的には解けないので、CMBfastやCAMB(Webインタフェース)といったコンピュータによる計算が必要となる。しかし、そのようなコンピュータ・プログラムによる計算結果は、物理過程を理解する目的には有用ではない。したがって、この章では解析的に扱える流体近似を用いた計算を中心に行う。とはいえ、いくつかの数値積分は必要となる。流体近似は単純であるが、コンピュータによる正確な計算結果をほどよく再現できるという意味で現実的な近似となっている。ゆらぎにはスカラー型のものとテンソル型のものがある。本章ではテンソル型の摂動の計算もスカラー型の摂動と同じくらいページ数を割いて解説している。スカラー型摂動とテンソル型摂動は独立である。
第7章:マイクロ波で観た空の異方性
この章では観測される温度ゆらぎを記述する一般公式を導く。第6章で与えた宇宙論的摂動の進化の解析と組み合わせ、スカラー型摂動とテンソル型摂動のそれぞれについて多重極展開係数の計算を簡単化する近似法を紹介する。またマイクロ波背景放射の偏向も計算する。
NASAのマイクロ波観測衛星WMAPで得られた宇宙マイクロ背景輻射の全天分布

「WMAP Viewer」を使うといろいろな温度帯(周波数帯)で宇宙マイクロ波背景輻射のゆらぎを見ることができる。ぜひご覧いただきたい。
第8章:構造の成長
この章で第6章で計算した時刻以降、すなわち脱結合の時刻以降のゆらぎの進化を計算する。まずはじめに線形解析を使って摂動が小さい頃の進化を追う。その後、星や銀河や銀河団の存在を見れば明らかなように、時間経過に従い物質密度の摂動は線形近似が使えなくなるほど大きくなる。この章では冷たい暗黒物質とバリオン物質の膨張、そして収縮、その後ガス雲からなる原始銀河への凝縮、星の誕生までの過程が示される。
第9章:重力レンズ
重力レンズ効果には「強い重力レンズ効果」と「弱い重力レンズ効果」がある。前者は暗い天体の探査や銀河団の構造の研究、そしてハッブル定数の測定に用いられてきた。後者は密度ゆらぎの相関関数を測定するのに強力な手段となる可能性がある。そして最後に「宇宙ひも」による重力ポテンシャルの計算方法が示されるが、宇宙ひもの検出がきわめて難しいことを紹介している。
第10章:宇宙論的ゆらぎの起源としてのインフレーション
この章ではインフレーション理論が第6章から第9章の議論に与える影響を学ぶ。第4章で学んだインフレーション宇宙理論の最も面白いところは、インフレーション理論が、宇宙マイクロ波背景放射や宇宙の大規模構造で観測される宇宙論的ゆらぎの起源として、量子力学を用いた自然な説明を与えるところにある。将来的には、インフレーションで生成された重力波も観測される可能性がある。(参考記事:「宇宙誕生時の「重力波」観測 米チームが世界初 」)
第6章の「宇宙論的ゆらぎの進化」が特に重要だ。宇宙が膨張するにしたがってゆらぎも大きく成長し拡大していく。しかし斑(まだら)模様を風船の表面に描いた場合、風船の膨張に比例してまだら模様のサイズは大きくなるが、宇宙の膨張とゆらぎの成長は比例しているわけではない。第6章では宇宙の歴史を物質優勢期になるまでのゆらぎと、放射優勢期になるまでのゆらぎをそれぞれ考察し、双方の期間で得られた解をなめらかにつなぐ方法を学ぶのだ。ゆらぎの成長曲線を求めるわけである。この計算は僕にとって「雲形定規」を使って区間ごと曲線をなめらかにつないでいくようなイメージに思えた。
式の変形過程は難解で詳しいところまではとても理解することができない。物理的に無視してよい項はどんどんそぎ落とし、アクロバティックな項の置き換えが何度も行われていく。理論的に美しい数式は、あれよあれよという間に複雑なものへと変形されていく。ごりごりと解に向かって突き進む職人技を見せ付けられる感じだ。その式や項の物理的な意味を実感として手に取るように理解しているからこそできる数式変形なのだと僕は思った。
ワインバーグ博士が本書の英語版を書かれたのは2008年、75歳のときである。(現在81歳)老いてもなお最先端の宇宙論に果敢に挑み続ける博士の頭脳と気力が衰えていないことには驚嘆させられるばかりである。NHKの「神の数式」にも出演して熱く語っておられたので、博士の顔を覚えている方も多いことだろう。世界最高クラスのノーベル物理学賞の実力というのはこんなにすごいものかと本書を持つ手につい力が入ってしまった。
数式の変形を追うことはできなくても、場の量子論を学んだ人ならば何を計算しているのかという流れにはついていける本だと思う。僕のようなレベルでも読後の充実感は大いにあった。
今年の夏は僕にとって宇宙論に対する意識変革の季節となった。以前は「宇宙論は大ざっぱで、詳しい計算結果で示されないからあまり興味が持てない。」と思っていたのだがNHKの「宇宙白熱教室」がきっかけで現代宇宙論の意義が強烈に心に焼きついたのだ。
本書にチャレンジしてみたいという方は、こちらからお買い求めいただきたい。
「ワインバーグの宇宙論(上): ビッグバン宇宙の進化」
「ワインバーグの宇宙論(下): ゆらぎの形成と進化」


翻訳の元となった英語版はこちらである。2008年刊行。
「Cosmology: Steven Weinberg」

英語版がでてから5年経っているとはいえ内容は最新だ。ぜひ一度書店でお手にとってみてほしい。
そしてワインバーグ博士が1970年代にお書きになった本も載せておこう。
1972年に刊行された宇宙論の教科書はこちら。
「Gravitation and Cosmology: Steven Weinberg」

一般読者向けに1977年に刊行された本の日本語版と英語原書はこちら。英語版は1977年初版だが、以下のリンクで買えるのは1993年に刊行されたUpdated版である。もちろん日本語版もUpdted版の翻訳だ。Update版では1989年に打ち上げられてCOBE衛星による宇宙マイクロ波背景放射の観測についても補足されているそうだ。
「宇宙創世はじめの3分間 (ちくま学芸文庫)」(レビュー記事)
「The First Three Minutes: A Modern View Of The Origin Of The Universe」(Kindle版)


関連記事:
宇宙論(上)ビッグバン宇宙の進化:S. ワインバーグ
https://blog.goo.ne.jp/ktonegaw/e/bd3d49fe1e13bcdd97116b33e8c736bb
発売情報:ワインバーグの宇宙論(上)(下)
https://blog.goo.ne.jp/ktonegaw/e/3aab4560e20f675285c35002fc96dfab
宇宙が始まる前には何があったのか?: ローレンス・クラウス
https://blog.goo.ne.jp/ktonegaw/e/b6f36e8eedba5ee63a4f919d30a2cb20
宇宙創世はじめの3分間 (ちくま学芸文庫):S. ワインバーグ
https://blog.goo.ne.jp/ktonegaw/e/cd00222f81ac344af10061b48e4d289d
大著に挑む (ワインバーグの「場の量子論」)
https://blog.goo.ne.jp/ktonegaw/e/95ac4b64aa4eaf70608088006813cbf5
応援クリックをお願いします!

「ワインバーグの宇宙論(下): ゆらぎの形成と進化」

第5章 小さなゆらぎの一般論
5.1 場の方程式
5.2 フーリエ分解と確率的初期条件
5.3 ゲージを選ぶ
5.4 地平線の外側での保存
第6章 宇宙論的ゆらぎの進化
6.1 スカラー型摂動──運動学的理論
6.2 スカラー型摂動──流体力学的極限
6.3 スカラー型摂動──長波長領域
6.4 スカラー型摂動──短波長領域
6.5 スカラー型摂動──内挿と輸送関数
6.6 テンソル型摂動
第7章 マイクロ波で観た空の異方性
7.1 温度ゆらぎの一般公式
7.2 温度の多重極展開の係数:スカラーモード
7.3 温度の多重極展開の係数:テンソルモード
7.4 偏光
第8章 構造の成長
8.1 再結合後の線形摂動論
8.2 非線形成長
8.3 バリオン物質の重力崩壊
第9章 重力レンズ
9.1 質点のレンズ方程式
9.2 増光:強いレンズとマイクロレンズ
9.3 広がったレンズ
9.4 時間の遅れ
9.5 弱い重力レンズ
9.6 宇宙ひも
第10章 宇宙論的ゆらぎの起源としてのインフレーション
10.1 インフレーション中のスカラー場のゆらぎ
10.2 インフレーション中のテンソル場のゆらぎ
10.3 インフレーション中のゆらぎ:スローロール近似
10.4 多重場インフレーション
付録B 一般相対性理論の復習
付録C 放射と電子間のエネルギー輸送
付録D エルゴード定理
付録E ガウス分布
付録F ニュートン力学的宇宙論
用語集
例題集
























微小項でも共鳴などが起こると影響も小さいとは限らないから面倒なんです。
コメントありがとうございます。
微小項というのはややもすると共鳴したりして無視できなくなる場合もあるのですね。
ワインバーグ博士もきっとそのあたりも十分に確認したうえで本書の微小項を無視したのだと思いました。
エロイカさんの紹介でここにきました。
今宇宙の勉強をするために、超準解析の独学中です。
数学はとても面白いので、これからもずっと勉強したいと思っています。
はじめまして。コメントいただき、ありがとうございました。
超準解析ですか。僕はまだ勉強はじめていませんが、あこがれのテーマのひとつです。
学びに終わりはありません。お互いがんばりましょう。
コメントありがとうございます。文章が最後のところで途中になってしまっていますが、きっと
n>mのすべてのnについて、|Xnーa|<εとなる
とお書きになりたかったのですよね。
このあたりのことは次のページをお読みになると理解できると思いますよ。
http://homepage3.nifty.com/rikei-index01/biseki/bisekiteiri1.html
あとε-δ論法の説明については「物理数学の直観的方法(ブルーバックス)」がわかりやすいです。
コメントいただきましたが、文章が途中で切れていますよ。
いえいえ、とんでもないです。
相変わらず文章は途中で途切れていますが、その理由がわかりました。
このコメント欄には不等号記号を半角文字で入力するとHTMLタグだと誤解されて、表示されないのです。(コメント欄にHTMLタグは入力できない仕様になっています。)
ですので、不等号記号を入力するときは全角文字の不等号を使えば文章をすべて表示させることができるようになります。たとえば>、<、≦、≧のように全角文字にします。
イプシロン-デルタ論法の最初の部分がおわかりにならないのですね。
適当な正の数δを決めると、そのδより小さくてゼロより大きい数が必ず存在しますからそれを|Xーa|と置くという意味です。
イプシロン-デルタ論法は次の動画やページを見ると理解できるようになると思いますよ。
動画:【微分積分】関数の連続性(イプシロン・デルタ論法)
https://www.youtube.com/watch?v=I0htQLgpsTE
ε-δ論法 その1「極限」
http://www2.odn.ne.jp/dokatin/ipusipon1.html
高校生のイプシロンデルタ - 数列の極限
http://www.ab.auone-net.jp/~visitors/_userdata/daigaku/kaiseki/suretukyokugen.pdf
ところで、いま、√2=1.41421356‥という無理数を例にとって、1.14,1.41,1.414,1.4142,‥という数列Xnを考えてみる。この数列の各項はいずれも有限小数で、有理数である。しかも、X1<X2<X3<‥
すべてのnについて、Xn<C (Cは定数)
という性質をもっている。という部分の意味ってなんですか?教えてください。
このブログのコメント欄は、数学や物理の問題の解き方や意味を相談する場所ではありません。
ご自分でお考えいただきますようお願いします。