マクスウェル方程式を１本にまとめたのは誰？

相対論的マクスウェル方程式のTシャツ

「EMANの物理学」や「趣味で物理学シリーズ」でおなじみの広江克彦さんは、最近物理学グッズの物販にも活動の幅を広げていらっしゃっている。掲載画像のような新商品を発売された。

Eman Physics - 物理学ライフを楽しくします。（物販サイト）
http://emanphysics.saleshop.jp/


1864年にジェームズ・クラーク・マクスウェルが数学的形式として整理し導いたマクスウェルの方程式は下のTシャツに書かれている４本の式であらわされ、これは電磁気学の基礎方程式である。この方程式からマクスウェルは電磁波の存在を予言し、1888年にヘルツによって電磁波は実証された。（参考ページ： 「電波は誰が発見したの？」）



４本の式であらわされるマクスウェル方程式によって古典電磁気学は確立した。けれどもその後、1905年にアインシュタインが特殊相対論を発表し、時空の概念に大変革がもたらされた。つまりこの世界は３次元の空間と１次元の時間で構成されているのではなく、空間と時間が一体となった４次元の「時空」として存在していることが発見されたのである。空間と時間は互いに関連をもちながら存在していたのだ。

マクスウェルの方程式は空間と時間の中でおきる電磁気現象を記述しているのだから、時空概念の大変革によって影響を受けてしまう。つじつまが合うように書き換えなければならない。実際に計算してみると不思議な結果が得られた。

マクスウェルの方程式に電磁ポテンシャルを導入して、相対論的（時空の４次元の形にする）にまとめると、なんとたった１本の式に集約されてしまうのだ。



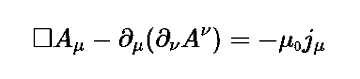
トップの掲載画像は新商品のTシャツで、１本にまとめられた方程式がプリントされている。電磁気学の４つの法則が４次元の時空では１つに見えることをあらわしている非常に美しい方程式だ。




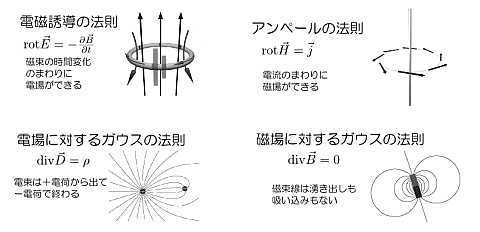
しかし式の導出方法は物理学専攻の学生にとっては特に難しいものではない。EMANの物理学では次のように導出している。

ステップ１）電磁ポテンシャル（EMANの電磁気学）
http://eman-physics.net/electromag/potential.html

ステップ２）ゲージ変換（EMANの電磁気学）
http://eman-physics.net/electromag/gauge.html

ステップ３）相対論的なマクスウェル方程式（EMANの相対性理論）
http://eman-physics.net/relativity/maxwell.html


でも世界で初めてこの式の導出を行ったのは誰なのだろう？そうツイートしたところ、広江さんもご存知でないようだった。



ええっ、広江さんも知らないの？？

アインシュタインが生まれた1879年にマクスウェルは亡くなっているのだから、この式を導いたのはもちろんマクスウェルではない。相対性理論を導いたアインシュタインでもないだろうし、ましてその先の相対論的量子力学を始めたディラックでもなさそうだ。導出手順は比較的やさしいので、論文で発表するほどでもなかったのだろうか？

捜索範囲は特殊相対論が発表された1905年からおそらく1925年あたりまでということになる。

「アインシュタイン選集１」と「アインシュタイン選集２」を調べてみた。特殊相対論を発表したころアインシュタインの電気力学は電磁ポテンシャルやテンソルを使わない形で書かれていたし、テンソル計算が使われている一般相対論の論文に電気力学についてのものは見当たらなかった。

もしこの式の歴史的背景や初めて導いたのが誰なのかご存知の方がいらっしゃったら、ぜひ教えていただきたい。

----------
その後、広江さんから次のことをツイッターでご連絡いただきました。

ワイルが1918年に、「電磁気、重力の統一の試みにゲージ理論を考案使用」とありますね。　「電磁気学への一般相対論の手法導入への挑戦」とも。　(今は見られなくなっているオヤオヤ文庫さんのサイト情報です）

ベクトルポテンシャルの意義が見直されるのがいつ頃かというのも関係ありそうですね。　ゲージ変換はもっと早めに行われていそうですけど。

参考文献は、湯川秀樹　井上健編集 世界の名著６６　現代の科学II（中央公論社）１９７０　だそうです。

ワイルの「空間・時間・物質（ちくま学芸文庫）」を確認してみたところ、なるほど下巻の最後のほうの「§40 電磁場の幾何学的表現」というセクションに重力場における電磁場の式が導出されていました。しかし、これは一般相対論と電磁場の統一のことです。今知りたいのは特殊相対論と電磁場の統一の式です。

また、たくさんの物理学書を翻訳された樺沢宇紀先生は次のようにツイートされています。

「ダランベルシャン記号（□ (⧠））を最初に使ったのは誰か？というのも気になるなあ。クライン＝ゴルドンあたりかなあ？（完全なあてずっぽう）教えてもらいたい。」

「４元ポテンシャルの式は不明ですが、A.パイスのアインシュタイン評伝『神は老獪にして・・・』の中に、ミンコフスキーの1908年の論文で「マクスウェル-ローレンツ方程式が初めて現代のテンソル形式で提示され」たという記述あり（p193）。」

「実質的にローレンツ条件下での?Ａ＝－ｊに相当する式は、ポアンカレの1905年の論文に既に見られますね（式(1)）。テンソル形式では書き下してないみたい（？）。
https://en.wikisource.org/?curid=664793#.C2.A7_1._.E2.80.94_Lorentz_transformation」

そしてツイッターやFacebookでお世話になっているおがわけんたろうさんは、次のようにおっしゃっています。

「さらに微分形式に翻訳したのは誰なんだろう。ここまでまとまるともう一歩ですよね。」

例えばマクスウェル方程式を「微分形式」で書くと・・・

dF = 0
d * F = J

これだけで済んでしまいます。（参考ツイート）

マクスウェル方程式の微分形式・外微分表現
挫折しない微分幾何学（リーマン幾何学）
https://yamakatsusan.web.fc2.com/maxwell.html

「この辺の歴史の本あっても良いと言うか・・・調べてまとめると好事家の興味は引きそうなんですが、問題はどの分野がどの時期に現代に通用するように整備されたかとかそういうのも関係しそうで、かなり広範な知識と調査が必要そうですね。誰かそういう仕事やらない・・・よなあｗ」

「当初の目的と言う論点では、ポアンカレの論文と言うことで良さそうですね。テンソル形式は少し調べてみれば結構さくっと出てきそう。微分形式の場合は、おそらくゲージ理論と微分幾何学の接点、解析力学あたりを突っ込んでいかないと・・・こりゃ深そう。」

「太田氏の電磁気学の基礎II」489ページのミンコフスキーの1908年の…と言うのは、これと思われる。おそらく共変形式はこれが初出であろうと思いますがどうでしょう。
https://en.m.wikisource.org/wiki/Translation:The_Fundamental_Equations_for_Electromagnetic_Processes_in_Moving_Bodies」

---------------------
2017年11月15日に追記：

ついにドイツ語の原論文が見つかりました。ツイッターでフォローさせていただいている中嶋慧さん（@subarusatosi）さんから教えていただきました。ありがとうございます！

最初に共変的に書いたのは、1908年の
H. Minkowski, Die Grundgleichungen fur die elektromagnetischen Vorgange in bewegten Korpern,
Minkowski1908a.pdf： リンク１　リンク２

だと思われます。
これは、太田浩一『マクスウェル理論の基礎』の文献[312]で、この本の10章の最初に、これが初だと書いてあります。


あとはダランベルシャン記号（□ (⧠））を使って、式を１本に最初にまとめたのは誰か？また、テンソル形式で最初に表記したのは誰か？という疑問が未解決だ。あともう一息である。

どうやら僕はパンドラの箱を開けてしまったようだ。

---------------------
2024年11月に追記：

コメント欄を通じ、浜村様から以下の情報をいただきました。ありがとうございます。

（マクスウェル方程式を１本にまとめたのは）ウィーン大学のフリードリッヒ⋅コトラー(1886-1965)で、1913年頃ではないか？

Friedrich Kottler のことは、下記の文献の111ページで知りました。

The Road to Relativity: The History and Meaning of Einstein's "The Foundation of General Relativity" Featuring the Original Manuscript of Einstein's Masterpiece
https://www.amazon.co.jp/Road-Relativity-Foundation-Manuscript-Masterpiece/dp/0691162530/

Friedrich Kottler (Wikipedia)
https://en.wikipedia.org/wiki/Friedrich_Kottler


関連記事：

趣味で物理学：広江克彦
https://blog.goo.ne.jp/ktonegaw/e/7faaca22d6b525d82e45a5724fef9811

趣味で相対論：広江克彦
https://blog.goo.ne.jp/ktonegaw/e/90aa60383b600ff4e4fd7bea6589deaa

趣味で量子力学：広江克彦
https://blog.goo.ne.jp/ktonegaw/e/3023098b9c5204d626808aa57823c16f

趣味で量子力学2（Kindle版、オンデマンド版）： 広江克彦
https://blog.goo.ne.jp/ktonegaw/e/0fdd36c5d70eaabc15ea5ae494a3955a


ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。