
「天体の回転について:コペルニクス著、矢島祐利訳」
明けましておめでとうございます。今年もよろしくお願いいたします。新年早々、長ったらしい記事を書いてしまいました。
「江戸で物理学を説く: ニュートン力学 」の記事の中で、僕は1600年代後半の江戸の町にタイムスリップしてしまい、まず地動説を実証することが必要になった。
地動説を唱えたコペルニクスのように、当時受け入れられていた天動説を僕は覆すことができるだろうか?彼はどのようにしてそれを成し得たのだろうか?それを知る必要がある。
そのためには「アインシュタインの相対性理論のとき」と同様、ご本人による著作を読むのがいちばんだ。何より著者の思考プロセスをありのままにたどることができる。天文学や物理学専攻の学生でも、さすがに本書のような古典を紐解く人は少ないだろう。しかし本書は科学史上の数ある名著のうち忘れてはならない1冊である。
クリックで拡大


原書は「Copernicus: De revolutionibus orbium coelestium (1543)」の全6巻。このうち第1巻だけが日本語訳され、昭和27年(1952年)に岩波文庫から出版された。翻訳者は科学史家の矢島祐利(やじますけとし)氏である。第1巻だけでコペルニクスの考えはほぼ尽くされている。後述した各巻目次に示したように第2巻から第6巻は天文学上の専門的な事柄、第1巻で述べた事項を具体的に実証するプロセスを解説している。
第1巻:太陽系の説明
第2巻:天球および日周運動の研究
第3巻:歳差の研究
第4巻:月の運行の研究
第5巻、第6巻:惑星運行論
翻訳本は現在絶版である。(復刊リクエスト)僕が100円で入手した中古本は昭和48年(1963年)の第4刷。川端康成の「伊豆の踊子」と同じくらい薄い文庫本だ。漢字は旧字体で7ポイントの小さな活字がびっしり。おまけに全ページわら半紙のように日に焼けているから原書に負けないくらい古く見える。
クリックで拡大
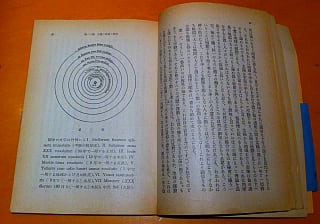
右ページをお読みいただくとわようにここが本書において太陽を中心に置いた地動説について結論している箇所だ。
全150ページのうち、前半86ページまでが第1巻の本編で、後半は翻訳者による解説であり、次の項目から構成されている。
1) コペルニクスの生涯(本書出版までのいきさつを含む)
2) コペルニクス以前の宇宙論
- 古代ギリシア、古代エジプト末期(年代順:イオニア学派、ピタゴラス学派、プラトン学派、エウドクソスの同心球説、アリストテレスの宇宙論、アリスタルコスの太陽中心説、エラトステネスの地球の測定、ヒッパルコスの周転円説、プトレマイオスの宇宙論)
- ローマ時代の宇宙観(暗黒の時代)
- 中世の宇宙論(古代ギリシア学術書の翻訳による学問の普及。ユークリッド幾何学、プトレマイオスの天文書(天動説)など)
3) コペルニクス説の発展
- コペルニクス説の反響
- ジョルダノ・ブルノ(コペルニクス説の信奉者。火刑にされた。)
- ティコ・ブラーエ(天体観測家。修正天動説考案。精密な観測結果を膨大に残した。)
- ヨハネス・ケプラー(コペルニクス説支持。ティコ・ブラーエの観測結果をもとにケプラーの3法則を提唱。)
- ガリレオ・ガリレイ(コペルニクス説支持。望遠鏡による天体観測。力学の基礎を築く。地動説を主張したため異端審問にかけられた。)
つまり、コペルニクスが地動説を唱える前まではプトレマイオスがその著書「アルマゲスト」としてまとめた天動説が信じられていた。
「アルマゲスト:プトレマイオス著、薮内清訳」

プトレマイオスの時代までには次のようなことがわかっていた。(xをつけたものは現代では誤りとされている。)
x 宇宙の中心は地球で、全ての天体が地球の周りを公転している。
x 地球から近い順に月、水星、金星、太陽、火星、木星、土星が回っている。
x 惑星の不規則な見かけの運動は大きな離心円と小さな周転円をいくつも組み合わせることによって可能になる。(離心円とは中心がずれた円のこと。楕円ではない。)
- 地球は球形で1日に1度の周期で自転している。
- 地球の緯度と経度、その天球上への投影した座標、つまり赤緯、赤経、天球の赤道、天球上の太陽の道筋としての黄道、そして天球座標としての黄緯、黄経が天体の位置の計算に使われていた。
- 黄道と赤道が一致していないので、地球の自転軸は天の北極に一致せず、その傾斜角が知られていた。
- 地球の大きさは不正確ながら求められていた。(全周が46500Kmと計算されていた。正しくは40000Km)
- 月、太陽、惑星の大まかな公転周期は長年の観測によって求められていた。
- 月や太陽、惑星までの距離は不正確ながら計算されていた。
- 月や太陽の大きさが不正確ながら計算されてれていた。
- 日食や月食の計算、予報が行われていた。
天動説はもちろん誤りであるが、古代ギリシアの時代からコペルニクスの時代に至るまでおよそ2000年間ずっとこの体系が信じられていた。
参考サイト:天動説(周転円説)と地動説との幾何学的関係
(Javaアプレットにより天動説、地動説それぞれの場合について月や惑星の運行を見ることができる。)
http://kakuda.ed.niigata-u.ac.jp/semi/ob/thesis/99niwata_thesis2-21/space/pto_fou/planet/planet.html
太陽系の惑星運行シミュレーション(コペルニクスの太陽中心モデルと、ティコ・ブラーエの地球中心モデルが比較できるようになっている。画像クリックで開く。)

そして順序が逆になったがコペルニクスによる本編第1巻の概要は次のとおりである。
第1章:宇宙は球形なること
宇宙は球形であり、この形こそ完全であり、太陽や月、星などすべてを含む最大容積をもつものであることが述べられている。
第2章:地もまた球形なること
地球も他の天体と同様に球形をしていることが述べられる。その根拠として次のことがあげられている。
- 北上するにつれて天球の北極が高くなること。
- 南北を隔てた場所により、見える星、見えない星が異なっていること。
- 遠ざかる船が水平線より下に沈むことから海面も球形の一部をなしていること。
第3章:地と水と共にいかにして球をなすか
地球全体の「土」と「水(海)」の比率についての解説。「土」の部分のほうが多いとしている。この章の解説は見当はずれなものだが、地球の中心へ向かう力(重力)が存在していることに言及していることを見逃してはならない。中心へ向かう力によって地球は球の形になっていることが主張されている。
第4章:天体の運動は一様で円いこと、あるいは円運動の合成なること
この章では次のことが解説されている。
- 太陽、月、惑星は球であり、球の自然な運動は「回転」であること。
- 天球の黄道上を太陽が1年かけて回る年周運動があり、それが1年の長さを決めること。
- 月は天球上を約1ヶ月かけて回り、それが1ヶ月の長さを決めること。
- 天球をはじめ太陽、月、惑星は日周運動をすること。
- 惑星は黄道に近い場所を動くが、その動きは順行、留、逆行など不定であること。
- 惑星の不定な動きにより、地球に近いとき(近地点)と遠いとき(遠地点)があること。
- 惑星の動きが遅いときは、それが地球から遠いときであり、早いときは地球から近いときであること。
- 太陽や月、そして惑星の不定な動きは円運動の組み合せによって説明可能なこと。(周転円理論:この章では天動説、地動説のどちらも主張していない。)
第5章:円運動は地球にもあてはまるか、またその場所
- 地球は球形であるからその自然な運動として回転(公転)する可能性が否定できないこと。だから地球が宇宙の中心ではない可能性がある。
- 地球は自転しているため、天球はじめ諸天体が日周運動すること。
- 地球を宇宙の中心以外の場所に置くことで、惑星の不定な運動、位置の遠近を説明することが可能である。
- 相対運動について。実際の運動と見かけの運動についての説明。
- 太陽や月についてもその運行が速くなったり遅くなったりすることが観測されていた。
- ピタゴラス学派の数学者フィロラオスは、地球が円運動すること、星のひとつに過ぎないと主張していた。
第6章:地球の大きさに較べて天の無限なること
- 天球の大きさは無限であるので、宇宙の中心が地球であってもなくても恒星の観測される位置に違いはないことを主張した。
- 土星は30年で天を1周し、月は1ヶ月で天を1周することが知られている。
- 宇宙の中心が地球であろうとなかろうと、天球の巨大さに比較するとその差は原子ほど小さいものである。(古代ギリシアのデモクリトスの原子論について言及されている。)
第7章:なぜ古代人は地球が不動で宇宙の中心であると考えたか
- 古代には重いものは地球の中心に向けて動き、軽いものは地球の中心から離れる方向に動くと考えられていた。
- 落下する物体の速度は増していくこと、すなわち加速度の概念が直観的に知られていた。
- 物の運動にはこのような上下の運動と中心に対する回転の運動の3種類あると考えられた。
- 回転運動の結果、遠心力が生じることが知られていた。
第8章:前章の理由の不十分なこと、および反論
- 古代には地球が回転(公転)するとその遠心力で地上の物体が破壊されるのでそれはあり得ない、すなわち地球は宇宙の中心に静止していると考えられていた。
- しかし、無限の広がりを持つ宇宙が回転すると考えることは、その遠心力が無限になるため、それは不可能なことだ。だから静止しているのは地球ではなく宇宙のほうである。
- 物の運動には上下の運動(落下と上昇)と中心に対する回転の運動の3種類あることが再度主張されている。
- 惑星は何かを中心として回転(公転)しているが、その中心が地球とは限らない。
第9章:地球にいろいろの運動を与え得るか、また宇宙の中心について
- 重力は地球以外に、太陽、月、惑星にもあることを主張。
- 太陽を宇宙の中心に置いても何ら矛盾は生じない。
- むしろそのほうが地球の年周運動により、惑星がほぼ1年毎に遠地点、近地点に来ること、それらの見かけの運動(順行、留、逆行など)を説明しやすくなる。
第10章:天体の軌道の順序
- 惑星の運動は遠いとき遅く見え、近いとき速く見える
- 惑星は遠いとき暗く見え、近いとき明るく見える。
- 惑星の輝きは太陽光線の反射である。
- 月までの距離は地球半径の64倍と計算した。(三角測量による。実際は60倍なのでかなり正確。)
- 太陽までの距離は地球半径の1160倍と計算した。(三角測量による。実際は2万3550倍なので不正確。)
- その他、水星、金星までの距離を不正確ながらも計算した。
- 水星、金星の軌道は地球の軌道の内側にあることにより、太陽からの離角が一定以上にならないことを示した。
- 太陽の周りを水星は80日、金星が9ヶ月、地球が1年、火星は2年、木星は12年、土星は30年で公転すること、そしてこれが太陽から各惑星までの距離の順番であることを主張した。(各惑星の公転周期は長年の観測によって古代から知られていた。)
- そして月は地球の周りを1ヶ月で公転し地球にいちばん近いことを述べた。
- 以上の計算、考察により太陽を中心とした地球、月、惑星を現代知られているのと同じ順序に配置した。これにより初めて正しい太陽系の惑星と月の配置が得られた。地動説の完成である。
クリックで拡大:
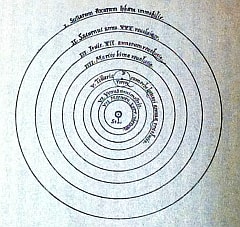
図中の文字は外側から
I. Stellarum fixarum sphaera immobilis (不動の恒星球)
II. Saturnus anno XXX reuoluitur (30年で一周する土星)
III. Iouis XII annorum reuolutio (12年で一周する木星)
IV. Martis bima reuolutio (2年で一周する火星)
V. Telluris cum orbe lunari annua reuolutio (1年で一周する地球および月の軌道)
VI. Venus nonimestris (9ヶ月で一周する金星)
VII. Mercury LXXX dierum (80日で一周する水星)
中央 Sol (太陽)
第11章:地球の三様の運動の証明
- 地球の三様の運動とは、自転、公転、歳差運動の3つをいう。
- 歳差運動とは地球の自転軸がコマのように回転することをいう。
- 歳差運動の周期はプトレマイオスの時代とコペルニクスの時代では21度の角度の違いがあることがわかっていた。
注意:恒星年と太陽年の差が,年々積み重なって1恒星年になるときが歳差運動の周期となるので 365.25636/(365.25636-365.24219)≒25776.7年 が正しい周期である。
第12章:円の弦の長さについて
- ギリシア、ローマの数字よりインドの数字を使ったほうが計算しやすいこと。
- 円や円弧、その弦や余弦、内接または外接する多角形の計算方法。
- 三角法による計算方法の解説。
第13章:平面三角形の辺と角について
- 平面幾何学の定理の解説。
第14章:球面三角形について
- 球面上に張り付いた三角形に成り立つ定理の解説。
ここまでが本編の概要であるが、以下の第2巻~第6巻の目次から、次のこともコペルニクスは理解していたことがわかる。(望遠鏡がガリレオによって発明されるのはコペルニクスの死後66年経った1609年であることに注意。)
- 春分点や秋分点の移動の観測により地球の歳差周期は比較的正確に計算されていた。
- 月の見かけの直径が変化すること。(月までの距離が一定でないこと。)
- 水星や金星の軌道は同一平面になく、軌道傾斜角が計算されていた。(しかし太陽から惑星までの距離が不正確なので軌道傾斜角も不正確である。)
- 水星や金星の軌道の中心がずれていることがわかっていた。(軌道の離心率という言葉が使われているが、軌道は円で中心がずれているものと考えていた。正しくは楕円軌道である。)
そして第2巻~第6巻では長年に渡る観測結果と計算結果との整合性が示され、地動説の正しさが詳細に検証されるのだ。
しかし、コペルニクスが到達できなかった事柄のうち、特に重要なのは次の3つである。
- 地球や月、惑星の軌道は円軌道だと理解していた。(正しくは楕円軌道。)
- 地球や惑星の公転周期はわかっていたが、公転半径が不正確なためケプラーの法則が導けなかった。(ケプラーにはなれなかった。)
- 地球や惑星が公転運動の原因がわからず、幾何学的な議論に終始していた。つまり天体の重力の存在には気づいていたが、公転運動と重力、力学との結びつきに思い至ることはなかった。(ニュートンにはなれなかった。)
ニコラウス・コペルニクスは1473年に生まれた。彼が18歳の1491年にクラクフ大学に入学し著名な天文学者で従天動説に懐疑的な見解を持っていたアルベルト・ブルゼフスキ教授と出会い、はじめて天文学に触れた。
当時、大学はキリスト教会に属していたので彼は聖職者としての道を進みながら神学はもちろん、天文学、算術、幾何学、測地学、力学、光学、法律学などを学ぶことになる。
1526年(コペルニクス53歳)にはクラクフ大学時代のブルゼフスキ教授の天文学の講座の同窓の親友で数学者のベルナルド・ヴァポフスキ がポーランド王国とリトアニア大公国の版図全体の地図を作成した際、コペルニクスはその事業を手伝った。一方で1535年、「地球の動き方」に関するコペルニクスの重要な論文の出版に向けてはヴァポフスキは力を貸し、出版を請け負っていたウィーンの関係者へ手紙を書いて出版の催促をするなどしている。ヴァポフスキはこの手紙を出した2週間後に他界したため、論文の出版を見届けることはなかった。
自己の地動説の発表による影響を恐れたコペルニクスは、主著『天体の回転について』の販売を1543年(コペルニクス70歳)に死期を迎えるまで許さなかった。彼自身は完成した書物を見る事無く逝ったと言われている。
臨終の床にあるコペルニクスにとってケプラーは28年後、ニュートンは99年後に生まれる未来人である。
コペルニクスの偉大さは次の2つに集約される。
- それまで2000年間信じられてきた「天動説という常識」は彼自身も学び、身についていたにもかかわらず、科学的な考察と実際の観測による計算の積み重ねによって、全くそれに反する「地動説」を導いたこと。
- 彼自身が所属するキリスト教会という巨大な組織による迫害を恐れずに著作を完成させたこと。その序文で当時の法王パウル3世に地動説の正当性を主張していること。
コペルニクスの地動説はその後長い間受け入れられることはなかった。キリスト教会の教義との矛盾については1992年、ローマ教皇ヨハネ・パウロ2世は、ガリレオ裁判が誤りであったことを認め、ガリレオに謝罪した。ガリレオの死去から実に350年後のことである。
また、ローマ教皇ベネディクト16世は2008年12月21日に行われた国連やユネスコが定めた「世界天文年2009」に関連した説教で、ガリレオらの業績を称え、地動説を改めて公式に認めている。
以上がコペルニクスおよび彼の地動説のあらましである。
最後に本書を翻訳した矢島祐利氏について触れておこう。僕はこの方についてよく知らなかったのだが、ウィキペディアの略歴から中学生のときに読んだファラデーの「ロウソクの科学」の翻訳者でもあることに気がついた。矢島氏は1995年にお亡くなりになっている。
またネットで調べていると、矢島氏の奥様は矢島せい子という有名な社会福祉運動家であり、彼女の妹は大女優の沢村貞子であることもわかった。
矢島祐利氏と奥様の矢島せい子氏のお写真:


矢島祐利の部(うずら文庫)
http://uzurabunko.com/suketoshi/suketoshi01.html
矢島せい子の部(うずら文庫)
http://uzurabunko.com/seiko/seiko.html
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。




「天体の回転について:コペルニクス著、矢島祐利訳」

全6巻の内容目次
第1巻:太陽系の説明
第1章:宇宙は球形なること
第2章:地もまた球形なること
第3章:地と水と共にいかにして球をなすか
第4章:天体の運動は一様で円いこと、あるいは円運動の合成なること
第5章:円運動は地球にもあてはまるか、またその場所
第6章:地球の大きさに較べて天の無限なること
第7章:なぜ古代人は地球が不動で宇宙の中心であると考えたか
第8章:前章の理由の不十分なこと、および反論
第9章:地球にいろいろの運動を与え得るか、また宇宙の中心について
第10章:天体の軌道の順序
第11章:地球の三様の運動の証明
第12章:円の弦の長さについて
第13章:平面三角形の辺と角について
第14章:球面三角形について
------ 本書はここまで ------------------------------------------
第2巻:天球および日周運動の研究
第1章:種々の円とその名称
第2章:黄道の傾斜・回帰の距離およびそれらの定め方
第3章:赤道・黄道・子午線の交点に対応する弧および角ならびにそれらによって赤緯および赤経を定めること
第4章:十二宮の真中を通る円(黄道)の外にあるが経度と緯度の分っている星の赤緯と赤経の定め方およびそれが黄道のどの点で空を二つに切るか
第5章:水平の断面
第6章:南(北)中の影の差異はいかなるものか
第7章:最も長い日、星の出の緯度、球の傾きはいかにして定まるか、および日のそのほかの差異
第8章:時間および昼夜の分かち
第9章:十二宮の傾き、或る原点に関しそれの定め方およびどの宮が空を二分するか
第10章:黄道と地平線との傾斜
第11章:表の使用について
第12章:水平面の両極を通り黄道に交わる諸円の角および周
第13章:星の出および入り
第14章:星の位置の研究および恒星の正しい記述
第3巻:歳差の研究
第1章:分点および二至の予見
第2章:変化する分点の歳差を打ち立てた観測の歴史
第3章:分点および黄道の傾きを証明する諸仮説
第4章:秤動はどうして円運動できるか
第5章:分点および傾きの予見の不規則なことの比較的の証明
第6章:分点の移動および黄道の傾きの変化の規則的な運動
第7章:分点の規則的な移動と見かけのそれとどちらが大きいか
第8章:それらの運動の特別の差異とその正しい現し方
第9章:歳差に関する現し方の検査と修正
第10章:分点と黄道の部分のうちどちらが大きいか
第11章:分点の一定の運動とアノマリ
第12章:春分点移動と傾斜変化の計算
第13章:太陽年の長さと違い
第14章:地球の中心の公転の規則的と平均の運動
第15章:太陽の運動の見かけの不規則性を証明するに役立つ諸原理
第16章:太陽の見かけの不規則性について
第17章:太陽の第一の、すなわち年週不規則ならびに特殊の差異
第18章:経度における規則的運動の検査について
第19章:太陽の運動が一様なるとき年中の場所および歳首を前もって定めることについて
第20章:地球からの距離の変化のために太陽の運動に伴う第二の、すなわち二重の違いについて
第21章:太陽の不規則の第二の違いの大きさは何程か
第22章:太陽の遠地点の規則的な運動および違った運動はいかにして説明されるか
第23章:太陽のアノマリの補正およびその場所を前もって定めることについて
第24章:一様性と見かけの差異の正しい現わし
第25章:太陽の見かけの計算について
第26章:自然日と違う昼夜の長さ
第4巻:惑星運行論
第1章:古代の人の意見による月の円の仮説
第2章:それらの人の意見の消滅について
第3章:月の運動に関する別の理論
第4章:月の公転およびその特殊の運動について
第5章:新月および満月に現れる月の第一の不規則性の証明
第6章:経度における月のアノマリの一様な運動の現わしの証明
第7章:経度における月のアノマリの位置
第8章:月の第二の違い、およびいかに第一の周転円が第二のに一致するかということ
第9章:月が周転円の最高点から不規則に動くように見えるところの第三の違いについて
第10章:月の見かけの運動がいかにして与えられたいくつかの一様な運動で記述されるか
第11章:プロスタフェレスつまり月の運動の不等の正しい現わし
第12章:月の運行の調べ
第13章:月の運動を緯度においていかに研究し記述するか
第14章:緯度におけるアノマリの位置
第15章:視差の機械の作り方
第16章:月のみちかけ
第17章:地球からの月の距離およびそれを地球の直径で現わすこと
第18章:月の地球へ投ずる影の直径とその経過
第19章:地球からの太陽および月の距離・それらの直径・月が通って行くときの影・影の軸をいかにして同時に明らかにするか
第20章:三つの天体すなわち太陽・月・地球の大きさおよびそれらの比較
第21章:太陽の見かけの直径およびその変化
第22章:月の見かけの直径およびその変化
第23章:地球の影の多様性をいかに説明するか
第24章:水平面の極を通る円のなかでの太陽および月の特殊の偏差の正しい現わし
第25章:太陽および月の視差の計算について
第26章:経度と緯度の視差をいかに区別するか
第27章:月の視差に関する現わしの確かめ
第28章:太陽と月の合および衝
第29章:太陽および月の真の合および衝の立入った研究
第30章:太陽および月の合および衝と黄道のその他の合および衝をいかに識別するか
第31章:日食および月食の広がりはどうであろうか
第32章:食がどれだけの時間続くか前もって知るために
第5巻:惑星運行論
第1章:惑星の回転と平均の運動について
第2章:古代の人の意見に従ったこれらの天体の見かけの一様性の証明
第3章:地球の運動による見かけの不等の一般的な証明
第4章:なぜ惑星の固有の運動は不等に見えるか
第5章:土星の運動の証明
第6章:夕方土星の近くに見える最近観測された三つの星について
第7章:土星の運動の調べについて
第8章:土星の位置の決定について
第9章:年毎に地球の軌道から遠ざかる土星の摂動について、また地球からその距離は何程か
第10章:木星の運動の証明
第11章:夕方木星の近くに見える最近観測された三つの星について
第12章:木星の一様な運動の証明
第13章:木星の位置の決定について
第14章:木星の摂動および地球公転に対するその高度の研究
第15章:惑星火星について
第16章:明け方火星の近くに見える最近観測された三つの星について
第17章:火星の運動の証明
第18章:火星の位置の決定
第19章:火星の軌道の大きさおよび地球の年週軌道についてのその見積り
第20章:惑星金星について
第21章:地球の軌道と金星のそれの比は何程であるか
第22章:金星の二つの運動について
第23章:金星の運動の調べについて
第24章:金星のアノマリの位置について
第25章:水星
第26章:水星の近地点および遠地点について
第27章:水星の離心率の大きさは何程か、またその軌道の対称はどうであるか
第28章:水星の離角はなぜ近地点に生ずるそれよりも六角形の一辺だけ(60度)大きく見えるか
第29章:水星の平均の運動の調べについて
第30章:最近観測された水星の運動について
第31章:水星の位置を前もって決定することについて
第32章:遠ざかりおよび近よりのもう一つの説明について
第33章:五つの惑星のプロスタフェレスの表
第34章:五つの惑星の位置を経度においていかに計算するか
第35章:五つの惑星の留および逆行について
第36章:逆行の時と位置をいかに識別するか
第6巻
第1章:五つの惑星の緯度における逆行を主題とする一般的叙述
第2章:惑星が緯度において動く円の仮説
第3章:土星・木星・火星の軌道の傾きの大きさは何程であるか
第4章:これらの三つの惑星の或る一般的な他の経度の現わしについて
第5章:金星および水星の経度について
第6章:金星および水星の近地点および遠地点におけるそれらの軌道の傾きによるそれらの緯度における第二の通過について
第7章:金星と水星の傾きの角は何程であるか
第8章:偏差と呼ぶ金星および水星の緯度における第三の状況について
第9章:五つの惑星の緯度の計算について
明けましておめでとうございます。今年もよろしくお願いいたします。新年早々、長ったらしい記事を書いてしまいました。
「江戸で物理学を説く: ニュートン力学 」の記事の中で、僕は1600年代後半の江戸の町にタイムスリップしてしまい、まず地動説を実証することが必要になった。
地動説を唱えたコペルニクスのように、当時受け入れられていた天動説を僕は覆すことができるだろうか?彼はどのようにしてそれを成し得たのだろうか?それを知る必要がある。
そのためには「アインシュタインの相対性理論のとき」と同様、ご本人による著作を読むのがいちばんだ。何より著者の思考プロセスをありのままにたどることができる。天文学や物理学専攻の学生でも、さすがに本書のような古典を紐解く人は少ないだろう。しかし本書は科学史上の数ある名著のうち忘れてはならない1冊である。
クリックで拡大


原書は「Copernicus: De revolutionibus orbium coelestium (1543)」の全6巻。このうち第1巻だけが日本語訳され、昭和27年(1952年)に岩波文庫から出版された。翻訳者は科学史家の矢島祐利(やじますけとし)氏である。第1巻だけでコペルニクスの考えはほぼ尽くされている。後述した各巻目次に示したように第2巻から第6巻は天文学上の専門的な事柄、第1巻で述べた事項を具体的に実証するプロセスを解説している。
第1巻:太陽系の説明
第2巻:天球および日周運動の研究
第3巻:歳差の研究
第4巻:月の運行の研究
第5巻、第6巻:惑星運行論
翻訳本は現在絶版である。(復刊リクエスト)僕が100円で入手した中古本は昭和48年(1963年)の第4刷。川端康成の「伊豆の踊子」と同じくらい薄い文庫本だ。漢字は旧字体で7ポイントの小さな活字がびっしり。おまけに全ページわら半紙のように日に焼けているから原書に負けないくらい古く見える。
クリックで拡大
右ページをお読みいただくとわようにここが本書において太陽を中心に置いた地動説について結論している箇所だ。

全150ページのうち、前半86ページまでが第1巻の本編で、後半は翻訳者による解説であり、次の項目から構成されている。
1) コペルニクスの生涯(本書出版までのいきさつを含む)
2) コペルニクス以前の宇宙論
- 古代ギリシア、古代エジプト末期(年代順:イオニア学派、ピタゴラス学派、プラトン学派、エウドクソスの同心球説、アリストテレスの宇宙論、アリスタルコスの太陽中心説、エラトステネスの地球の測定、ヒッパルコスの周転円説、プトレマイオスの宇宙論)
- ローマ時代の宇宙観(暗黒の時代)
- 中世の宇宙論(古代ギリシア学術書の翻訳による学問の普及。ユークリッド幾何学、プトレマイオスの天文書(天動説)など)
3) コペルニクス説の発展
- コペルニクス説の反響
- ジョルダノ・ブルノ(コペルニクス説の信奉者。火刑にされた。)
- ティコ・ブラーエ(天体観測家。修正天動説考案。精密な観測結果を膨大に残した。)
- ヨハネス・ケプラー(コペルニクス説支持。ティコ・ブラーエの観測結果をもとにケプラーの3法則を提唱。)
- ガリレオ・ガリレイ(コペルニクス説支持。望遠鏡による天体観測。力学の基礎を築く。地動説を主張したため異端審問にかけられた。)
つまり、コペルニクスが地動説を唱える前まではプトレマイオスがその著書「アルマゲスト」としてまとめた天動説が信じられていた。
「アルマゲスト:プトレマイオス著、薮内清訳」

プトレマイオスの時代までには次のようなことがわかっていた。(xをつけたものは現代では誤りとされている。)
x 宇宙の中心は地球で、全ての天体が地球の周りを公転している。
x 地球から近い順に月、水星、金星、太陽、火星、木星、土星が回っている。
x 惑星の不規則な見かけの運動は大きな離心円と小さな周転円をいくつも組み合わせることによって可能になる。(離心円とは中心がずれた円のこと。楕円ではない。)
- 地球は球形で1日に1度の周期で自転している。
- 地球の緯度と経度、その天球上への投影した座標、つまり赤緯、赤経、天球の赤道、天球上の太陽の道筋としての黄道、そして天球座標としての黄緯、黄経が天体の位置の計算に使われていた。
- 黄道と赤道が一致していないので、地球の自転軸は天の北極に一致せず、その傾斜角が知られていた。
- 地球の大きさは不正確ながら求められていた。(全周が46500Kmと計算されていた。正しくは40000Km)
- 月、太陽、惑星の大まかな公転周期は長年の観測によって求められていた。
- 月や太陽、惑星までの距離は不正確ながら計算されていた。
- 月や太陽の大きさが不正確ながら計算されてれていた。
- 日食や月食の計算、予報が行われていた。
天動説はもちろん誤りであるが、古代ギリシアの時代からコペルニクスの時代に至るまでおよそ2000年間ずっとこの体系が信じられていた。
参考サイト:天動説(周転円説)と地動説との幾何学的関係
(Javaアプレットにより天動説、地動説それぞれの場合について月や惑星の運行を見ることができる。)
http://kakuda.ed.niigata-u.ac.jp/semi/ob/thesis/99niwata_thesis2-21/space/pto_fou/planet/planet.html
太陽系の惑星運行シミュレーション(コペルニクスの太陽中心モデルと、ティコ・ブラーエの地球中心モデルが比較できるようになっている。画像クリックで開く。)

そして順序が逆になったがコペルニクスによる本編第1巻の概要は次のとおりである。
第1章:宇宙は球形なること
宇宙は球形であり、この形こそ完全であり、太陽や月、星などすべてを含む最大容積をもつものであることが述べられている。
第2章:地もまた球形なること
地球も他の天体と同様に球形をしていることが述べられる。その根拠として次のことがあげられている。
- 北上するにつれて天球の北極が高くなること。
- 南北を隔てた場所により、見える星、見えない星が異なっていること。
- 遠ざかる船が水平線より下に沈むことから海面も球形の一部をなしていること。
第3章:地と水と共にいかにして球をなすか
地球全体の「土」と「水(海)」の比率についての解説。「土」の部分のほうが多いとしている。この章の解説は見当はずれなものだが、地球の中心へ向かう力(重力)が存在していることに言及していることを見逃してはならない。中心へ向かう力によって地球は球の形になっていることが主張されている。
第4章:天体の運動は一様で円いこと、あるいは円運動の合成なること
この章では次のことが解説されている。
- 太陽、月、惑星は球であり、球の自然な運動は「回転」であること。
- 天球の黄道上を太陽が1年かけて回る年周運動があり、それが1年の長さを決めること。
- 月は天球上を約1ヶ月かけて回り、それが1ヶ月の長さを決めること。
- 天球をはじめ太陽、月、惑星は日周運動をすること。
- 惑星は黄道に近い場所を動くが、その動きは順行、留、逆行など不定であること。
- 惑星の不定な動きにより、地球に近いとき(近地点)と遠いとき(遠地点)があること。
- 惑星の動きが遅いときは、それが地球から遠いときであり、早いときは地球から近いときであること。
- 太陽や月、そして惑星の不定な動きは円運動の組み合せによって説明可能なこと。(周転円理論:この章では天動説、地動説のどちらも主張していない。)
第5章:円運動は地球にもあてはまるか、またその場所
- 地球は球形であるからその自然な運動として回転(公転)する可能性が否定できないこと。だから地球が宇宙の中心ではない可能性がある。
- 地球は自転しているため、天球はじめ諸天体が日周運動すること。
- 地球を宇宙の中心以外の場所に置くことで、惑星の不定な運動、位置の遠近を説明することが可能である。
- 相対運動について。実際の運動と見かけの運動についての説明。
- 太陽や月についてもその運行が速くなったり遅くなったりすることが観測されていた。
- ピタゴラス学派の数学者フィロラオスは、地球が円運動すること、星のひとつに過ぎないと主張していた。
第6章:地球の大きさに較べて天の無限なること
- 天球の大きさは無限であるので、宇宙の中心が地球であってもなくても恒星の観測される位置に違いはないことを主張した。
- 土星は30年で天を1周し、月は1ヶ月で天を1周することが知られている。
- 宇宙の中心が地球であろうとなかろうと、天球の巨大さに比較するとその差は原子ほど小さいものである。(古代ギリシアのデモクリトスの原子論について言及されている。)
第7章:なぜ古代人は地球が不動で宇宙の中心であると考えたか
- 古代には重いものは地球の中心に向けて動き、軽いものは地球の中心から離れる方向に動くと考えられていた。
- 落下する物体の速度は増していくこと、すなわち加速度の概念が直観的に知られていた。
- 物の運動にはこのような上下の運動と中心に対する回転の運動の3種類あると考えられた。
- 回転運動の結果、遠心力が生じることが知られていた。
第8章:前章の理由の不十分なこと、および反論
- 古代には地球が回転(公転)するとその遠心力で地上の物体が破壊されるのでそれはあり得ない、すなわち地球は宇宙の中心に静止していると考えられていた。
- しかし、無限の広がりを持つ宇宙が回転すると考えることは、その遠心力が無限になるため、それは不可能なことだ。だから静止しているのは地球ではなく宇宙のほうである。
- 物の運動には上下の運動(落下と上昇)と中心に対する回転の運動の3種類あることが再度主張されている。
- 惑星は何かを中心として回転(公転)しているが、その中心が地球とは限らない。
第9章:地球にいろいろの運動を与え得るか、また宇宙の中心について
- 重力は地球以外に、太陽、月、惑星にもあることを主張。
- 太陽を宇宙の中心に置いても何ら矛盾は生じない。
- むしろそのほうが地球の年周運動により、惑星がほぼ1年毎に遠地点、近地点に来ること、それらの見かけの運動(順行、留、逆行など)を説明しやすくなる。
第10章:天体の軌道の順序
- 惑星の運動は遠いとき遅く見え、近いとき速く見える
- 惑星は遠いとき暗く見え、近いとき明るく見える。
- 惑星の輝きは太陽光線の反射である。
- 月までの距離は地球半径の64倍と計算した。(三角測量による。実際は60倍なのでかなり正確。)
- 太陽までの距離は地球半径の1160倍と計算した。(三角測量による。実際は2万3550倍なので不正確。)
- その他、水星、金星までの距離を不正確ながらも計算した。
- 水星、金星の軌道は地球の軌道の内側にあることにより、太陽からの離角が一定以上にならないことを示した。
- 太陽の周りを水星は80日、金星が9ヶ月、地球が1年、火星は2年、木星は12年、土星は30年で公転すること、そしてこれが太陽から各惑星までの距離の順番であることを主張した。(各惑星の公転周期は長年の観測によって古代から知られていた。)
- そして月は地球の周りを1ヶ月で公転し地球にいちばん近いことを述べた。
- 以上の計算、考察により太陽を中心とした地球、月、惑星を現代知られているのと同じ順序に配置した。これにより初めて正しい太陽系の惑星と月の配置が得られた。地動説の完成である。
クリックで拡大:

図中の文字は外側から
I. Stellarum fixarum sphaera immobilis (不動の恒星球)
II. Saturnus anno XXX reuoluitur (30年で一周する土星)
III. Iouis XII annorum reuolutio (12年で一周する木星)
IV. Martis bima reuolutio (2年で一周する火星)
V. Telluris cum orbe lunari annua reuolutio (1年で一周する地球および月の軌道)
VI. Venus nonimestris (9ヶ月で一周する金星)
VII. Mercury LXXX dierum (80日で一周する水星)
中央 Sol (太陽)
第11章:地球の三様の運動の証明
- 地球の三様の運動とは、自転、公転、歳差運動の3つをいう。
- 歳差運動とは地球の自転軸がコマのように回転することをいう。
- 歳差運動の周期はプトレマイオスの時代とコペルニクスの時代では21度の角度の違いがあることがわかっていた。
注意:恒星年と太陽年の差が,年々積み重なって1恒星年になるときが歳差運動の周期となるので 365.25636/(365.25636-365.24219)≒25776.7年 が正しい周期である。
第12章:円の弦の長さについて
- ギリシア、ローマの数字よりインドの数字を使ったほうが計算しやすいこと。
- 円や円弧、その弦や余弦、内接または外接する多角形の計算方法。
- 三角法による計算方法の解説。
第13章:平面三角形の辺と角について
- 平面幾何学の定理の解説。
第14章:球面三角形について
- 球面上に張り付いた三角形に成り立つ定理の解説。
ここまでが本編の概要であるが、以下の第2巻~第6巻の目次から、次のこともコペルニクスは理解していたことがわかる。(望遠鏡がガリレオによって発明されるのはコペルニクスの死後66年経った1609年であることに注意。)
- 春分点や秋分点の移動の観測により地球の歳差周期は比較的正確に計算されていた。
- 月の見かけの直径が変化すること。(月までの距離が一定でないこと。)
- 水星や金星の軌道は同一平面になく、軌道傾斜角が計算されていた。(しかし太陽から惑星までの距離が不正確なので軌道傾斜角も不正確である。)
- 水星や金星の軌道の中心がずれていることがわかっていた。(軌道の離心率という言葉が使われているが、軌道は円で中心がずれているものと考えていた。正しくは楕円軌道である。)
そして第2巻~第6巻では長年に渡る観測結果と計算結果との整合性が示され、地動説の正しさが詳細に検証されるのだ。
しかし、コペルニクスが到達できなかった事柄のうち、特に重要なのは次の3つである。
- 地球や月、惑星の軌道は円軌道だと理解していた。(正しくは楕円軌道。)
- 地球や惑星の公転周期はわかっていたが、公転半径が不正確なためケプラーの法則が導けなかった。(ケプラーにはなれなかった。)
- 地球や惑星が公転運動の原因がわからず、幾何学的な議論に終始していた。つまり天体の重力の存在には気づいていたが、公転運動と重力、力学との結びつきに思い至ることはなかった。(ニュートンにはなれなかった。)
ニコラウス・コペルニクスは1473年に生まれた。彼が18歳の1491年にクラクフ大学に入学し著名な天文学者で従天動説に懐疑的な見解を持っていたアルベルト・ブルゼフスキ教授と出会い、はじめて天文学に触れた。
当時、大学はキリスト教会に属していたので彼は聖職者としての道を進みながら神学はもちろん、天文学、算術、幾何学、測地学、力学、光学、法律学などを学ぶことになる。
1526年(コペルニクス53歳)にはクラクフ大学時代のブルゼフスキ教授の天文学の講座の同窓の親友で数学者のベルナルド・ヴァポフスキ がポーランド王国とリトアニア大公国の版図全体の地図を作成した際、コペルニクスはその事業を手伝った。一方で1535年、「地球の動き方」に関するコペルニクスの重要な論文の出版に向けてはヴァポフスキは力を貸し、出版を請け負っていたウィーンの関係者へ手紙を書いて出版の催促をするなどしている。ヴァポフスキはこの手紙を出した2週間後に他界したため、論文の出版を見届けることはなかった。
自己の地動説の発表による影響を恐れたコペルニクスは、主著『天体の回転について』の販売を1543年(コペルニクス70歳)に死期を迎えるまで許さなかった。彼自身は完成した書物を見る事無く逝ったと言われている。
臨終の床にあるコペルニクスにとってケプラーは28年後、ニュートンは99年後に生まれる未来人である。
コペルニクスの偉大さは次の2つに集約される。
- それまで2000年間信じられてきた「天動説という常識」は彼自身も学び、身についていたにもかかわらず、科学的な考察と実際の観測による計算の積み重ねによって、全くそれに反する「地動説」を導いたこと。
- 彼自身が所属するキリスト教会という巨大な組織による迫害を恐れずに著作を完成させたこと。その序文で当時の法王パウル3世に地動説の正当性を主張していること。
コペルニクスの地動説はその後長い間受け入れられることはなかった。キリスト教会の教義との矛盾については1992年、ローマ教皇ヨハネ・パウロ2世は、ガリレオ裁判が誤りであったことを認め、ガリレオに謝罪した。ガリレオの死去から実に350年後のことである。
また、ローマ教皇ベネディクト16世は2008年12月21日に行われた国連やユネスコが定めた「世界天文年2009」に関連した説教で、ガリレオらの業績を称え、地動説を改めて公式に認めている。
以上がコペルニクスおよび彼の地動説のあらましである。
最後に本書を翻訳した矢島祐利氏について触れておこう。僕はこの方についてよく知らなかったのだが、ウィキペディアの略歴から中学生のときに読んだファラデーの「ロウソクの科学」の翻訳者でもあることに気がついた。矢島氏は1995年にお亡くなりになっている。
またネットで調べていると、矢島氏の奥様は矢島せい子という有名な社会福祉運動家であり、彼女の妹は大女優の沢村貞子であることもわかった。
矢島祐利氏と奥様の矢島せい子氏のお写真:


矢島祐利の部(うずら文庫)
http://uzurabunko.com/suketoshi/suketoshi01.html
矢島せい子の部(うずら文庫)
http://uzurabunko.com/seiko/seiko.html
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。

「天体の回転について:コペルニクス著、矢島祐利訳」

全6巻の内容目次
第1巻:太陽系の説明
第1章:宇宙は球形なること
第2章:地もまた球形なること
第3章:地と水と共にいかにして球をなすか
第4章:天体の運動は一様で円いこと、あるいは円運動の合成なること
第5章:円運動は地球にもあてはまるか、またその場所
第6章:地球の大きさに較べて天の無限なること
第7章:なぜ古代人は地球が不動で宇宙の中心であると考えたか
第8章:前章の理由の不十分なこと、および反論
第9章:地球にいろいろの運動を与え得るか、また宇宙の中心について
第10章:天体の軌道の順序
第11章:地球の三様の運動の証明
第12章:円の弦の長さについて
第13章:平面三角形の辺と角について
第14章:球面三角形について
------ 本書はここまで ------------------------------------------
第2巻:天球および日周運動の研究
第1章:種々の円とその名称
第2章:黄道の傾斜・回帰の距離およびそれらの定め方
第3章:赤道・黄道・子午線の交点に対応する弧および角ならびにそれらによって赤緯および赤経を定めること
第4章:十二宮の真中を通る円(黄道)の外にあるが経度と緯度の分っている星の赤緯と赤経の定め方およびそれが黄道のどの点で空を二つに切るか
第5章:水平の断面
第6章:南(北)中の影の差異はいかなるものか
第7章:最も長い日、星の出の緯度、球の傾きはいかにして定まるか、および日のそのほかの差異
第8章:時間および昼夜の分かち
第9章:十二宮の傾き、或る原点に関しそれの定め方およびどの宮が空を二分するか
第10章:黄道と地平線との傾斜
第11章:表の使用について
第12章:水平面の両極を通り黄道に交わる諸円の角および周
第13章:星の出および入り
第14章:星の位置の研究および恒星の正しい記述
第3巻:歳差の研究
第1章:分点および二至の予見
第2章:変化する分点の歳差を打ち立てた観測の歴史
第3章:分点および黄道の傾きを証明する諸仮説
第4章:秤動はどうして円運動できるか
第5章:分点および傾きの予見の不規則なことの比較的の証明
第6章:分点の移動および黄道の傾きの変化の規則的な運動
第7章:分点の規則的な移動と見かけのそれとどちらが大きいか
第8章:それらの運動の特別の差異とその正しい現し方
第9章:歳差に関する現し方の検査と修正
第10章:分点と黄道の部分のうちどちらが大きいか
第11章:分点の一定の運動とアノマリ
第12章:春分点移動と傾斜変化の計算
第13章:太陽年の長さと違い
第14章:地球の中心の公転の規則的と平均の運動
第15章:太陽の運動の見かけの不規則性を証明するに役立つ諸原理
第16章:太陽の見かけの不規則性について
第17章:太陽の第一の、すなわち年週不規則ならびに特殊の差異
第18章:経度における規則的運動の検査について
第19章:太陽の運動が一様なるとき年中の場所および歳首を前もって定めることについて
第20章:地球からの距離の変化のために太陽の運動に伴う第二の、すなわち二重の違いについて
第21章:太陽の不規則の第二の違いの大きさは何程か
第22章:太陽の遠地点の規則的な運動および違った運動はいかにして説明されるか
第23章:太陽のアノマリの補正およびその場所を前もって定めることについて
第24章:一様性と見かけの差異の正しい現わし
第25章:太陽の見かけの計算について
第26章:自然日と違う昼夜の長さ
第4巻:惑星運行論
第1章:古代の人の意見による月の円の仮説
第2章:それらの人の意見の消滅について
第3章:月の運動に関する別の理論
第4章:月の公転およびその特殊の運動について
第5章:新月および満月に現れる月の第一の不規則性の証明
第6章:経度における月のアノマリの一様な運動の現わしの証明
第7章:経度における月のアノマリの位置
第8章:月の第二の違い、およびいかに第一の周転円が第二のに一致するかということ
第9章:月が周転円の最高点から不規則に動くように見えるところの第三の違いについて
第10章:月の見かけの運動がいかにして与えられたいくつかの一様な運動で記述されるか
第11章:プロスタフェレスつまり月の運動の不等の正しい現わし
第12章:月の運行の調べ
第13章:月の運動を緯度においていかに研究し記述するか
第14章:緯度におけるアノマリの位置
第15章:視差の機械の作り方
第16章:月のみちかけ
第17章:地球からの月の距離およびそれを地球の直径で現わすこと
第18章:月の地球へ投ずる影の直径とその経過
第19章:地球からの太陽および月の距離・それらの直径・月が通って行くときの影・影の軸をいかにして同時に明らかにするか
第20章:三つの天体すなわち太陽・月・地球の大きさおよびそれらの比較
第21章:太陽の見かけの直径およびその変化
第22章:月の見かけの直径およびその変化
第23章:地球の影の多様性をいかに説明するか
第24章:水平面の極を通る円のなかでの太陽および月の特殊の偏差の正しい現わし
第25章:太陽および月の視差の計算について
第26章:経度と緯度の視差をいかに区別するか
第27章:月の視差に関する現わしの確かめ
第28章:太陽と月の合および衝
第29章:太陽および月の真の合および衝の立入った研究
第30章:太陽および月の合および衝と黄道のその他の合および衝をいかに識別するか
第31章:日食および月食の広がりはどうであろうか
第32章:食がどれだけの時間続くか前もって知るために
第5巻:惑星運行論
第1章:惑星の回転と平均の運動について
第2章:古代の人の意見に従ったこれらの天体の見かけの一様性の証明
第3章:地球の運動による見かけの不等の一般的な証明
第4章:なぜ惑星の固有の運動は不等に見えるか
第5章:土星の運動の証明
第6章:夕方土星の近くに見える最近観測された三つの星について
第7章:土星の運動の調べについて
第8章:土星の位置の決定について
第9章:年毎に地球の軌道から遠ざかる土星の摂動について、また地球からその距離は何程か
第10章:木星の運動の証明
第11章:夕方木星の近くに見える最近観測された三つの星について
第12章:木星の一様な運動の証明
第13章:木星の位置の決定について
第14章:木星の摂動および地球公転に対するその高度の研究
第15章:惑星火星について
第16章:明け方火星の近くに見える最近観測された三つの星について
第17章:火星の運動の証明
第18章:火星の位置の決定
第19章:火星の軌道の大きさおよび地球の年週軌道についてのその見積り
第20章:惑星金星について
第21章:地球の軌道と金星のそれの比は何程であるか
第22章:金星の二つの運動について
第23章:金星の運動の調べについて
第24章:金星のアノマリの位置について
第25章:水星
第26章:水星の近地点および遠地点について
第27章:水星の離心率の大きさは何程か、またその軌道の対称はどうであるか
第28章:水星の離角はなぜ近地点に生ずるそれよりも六角形の一辺だけ(60度)大きく見えるか
第29章:水星の平均の運動の調べについて
第30章:最近観測された水星の運動について
第31章:水星の位置を前もって決定することについて
第32章:遠ざかりおよび近よりのもう一つの説明について
第33章:五つの惑星のプロスタフェレスの表
第34章:五つの惑星の位置を経度においていかに計算するか
第35章:五つの惑星の留および逆行について
第36章:逆行の時と位置をいかに識別するか
第6巻
第1章:五つの惑星の緯度における逆行を主題とする一般的叙述
第2章:惑星が緯度において動く円の仮説
第3章:土星・木星・火星の軌道の傾きの大きさは何程であるか
第4章:これらの三つの惑星の或る一般的な他の経度の現わしについて
第5章:金星および水星の経度について
第6章:金星および水星の近地点および遠地点におけるそれらの軌道の傾きによるそれらの緯度における第二の通過について
第7章:金星と水星の傾きの角は何程であるか
第8章:偏差と呼ぶ金星および水星の緯度における第三の状況について
第9章:五つの惑星の緯度の計算について
























新年おめでとうございます。
その後、このテーマについていろいろ本で調べているところです。ポイントはどれだけ精度の高い観測を行えるかですね。方位だけでなく、天体までの距離についてもです。
おっしゃるように、キリスト教が絶大な権力をふるっていた時代に反論を主張することは、命をかけた困難があったのですね。
そして、観測できたのは方向だけですから、各円の半径は任意に設定できます。
つまり、同位相で回転する円の半径を同じにすると太陽,全惑星は全く同じ回転をしているのです。
周りが同じ運動をしてたら自分が動いてると結論するのは当然のことですが、キリスト教が人間中心ですから困難ですね。
良さげなブログですね!またたく間に「お気に入り」になってしまいました。教えていただき、ありがとうございます。
今でも年に1~2度「天体望遠鏡欲しい。」という思いにとらわれることがあります。けれど、1台買うと、もっと性能の良いのが欲しくなるに決まってますから、そのたびに思いとどまっています。
次は、ちょっと、お勧めのブログです。
http://mononoke.asablo.jp/blog/2012/01/02/6275399
新年おめでとうございます。今年もよろしくお願いします。
僕も天動説や周転円のことを調べている時、フーリエ級数のことを考えていました。解析学が始まるのはコペルニクスよりもだいぶ後になるので「天動説+フーリエ級数理論」は実現し得ませんでしたが。
適当な関数を入力して、それからフーリエ級数を生成し、周転円の組み合せをグラフィック表示するJavaアプレットとか作ったら面白そうだと思いました。
コペルニクスやケプラーのことを調べているうちに昔かかった天文学熱が再燃してしまい、この正月は高校生の頃に買った古い天文学書籍を眺めながら空想に浸っています。(とねの本棚の天文のカテゴリーに登録しました。)それに飽き足らず(姪っ子のために)宇宙や星座の図鑑まで買ってしまいました。
書店に行って気がついたのですが、最近の天文書籍ってビジュアルなものがほとんどで、昔の天体観測シリーズや中級者向けの新天文学シリーズのような本、天体の軌道計算入門書のような本が無くなってしまいました。「はやぶさ」など探査機が惑星に直接行ったり、ハッブル望遠鏡のようにアマチュアが太刀打ちできないレベルまで天文学が発達したので、見るだけの本が増えてしまったのは仕方のないことでしょうけれど。それでも、もう少し一般向けの数理的な天文書が増えればよいのになと思っています。
mitakaというフリーソフトで遊ぶのも小学生、中高生にとっては大いに刺激になるのでお勧めだと思いました。こういうのが無料で手に入るのですね。隔世の感がします。
明日は仕事始めなので、宇宙から現実世界に引き戻されることになります。
今年もよろしくお願いします。
周期的運動は三角関数の和で表されるというフーリエ級数の考え方がもっと早く発見されていたかも知れません。