"5" で現れる不思議な形 (フェルマー点の話)
自然界には対称的な形をしたものがほとんどだ。太陽や地球も球であるし、惑星の軌道は楕円軌道なので線対称だ。地上に目をうつしても人間をはじめとする動物の体は左右対称だし、電磁波もきれいなサインカーブで線対称だ。ひまわりの花についている種はきれいな螺旋を描いているし、巻貝の美しい模様は回転対称的な自然の美を感じさせてくれる。
対称的なのはなにも「形」だけではない。磁石にはN極とS極があり、電気はプラスとマイナスがある。空間自体も3次元的に対称的だし時間には過去と未来という対称性がある。
神様は自然法則を作るにあたってどうも「対称性」をかなり意識したように思える。
ところが、ときおり神様はいたずらをして対称的でないものを私たちに見せてくれることがある。今日紹介するのはそのような「神様のいたずら」の一例だ。
----------------------
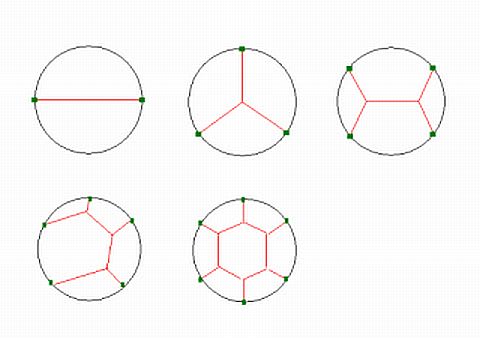
円形の透明なプラスチック板を2枚用意し、間に5ミリほどの空間ができるようにして固定する。プラスチック板の外周に小さな柱を取り付けて固定すればよい。
そのプラスチック円板が十分入るくらいの大きさの洗面器に石鹸水を入れておく。シャボン玉ができるくらいの濃さがよい。
円板の周囲に2本柱を取り付けたものを、石鹸水に沈めて静かに引き上げると柱と柱の間に石鹸水の膜ができる。円板を上から見ると、膜はこの図の赤線で示される。

石鹸膜は表面張力によって面積が最小になろうとするから、上から見た図で膜をあらわす赤い線は2つの柱を結ぶ直線になる。
次に柱の数を3本に増やして同じ実験をしたら石鹸膜はどのような形になるだろうか?このような形になるのだろうか?
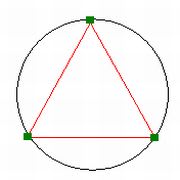
残念ながら、こうはならない。3つの柱を結ぶ線の長さを合計したものを最小にするためには、次のような形になるのだ。実験してみるとこのような膜があらわれる。円板の中に柱は立っていないのに石鹸膜をあらわす線は1点に集まってしまうのだ。

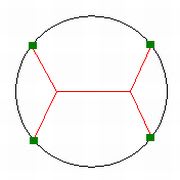
さらに柱の数を4本にするとどうだろうか?このような膜があらわれるだろうか?

これも不正解である。柱4本のときは、ちょっと不思議な膜ができるのだ。これが4つの柱を結ぶ膜の長さの合計が最小になる場合の答だ。
柱の数を5本にすると、さらに難しくなる。けれども自然にとっては何がやさしくて何が難しいかは関係ない。与えられた法則にしたがって形を決めるだけなのだから。5本のときはこのような膜があらわれるのだろうか?
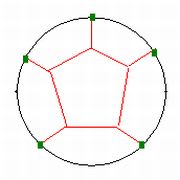
実はこれも不正解。柱が5本のときは、次のように不思議な形がでてきてしまうのだ。
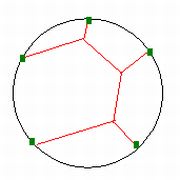
点対称でも線対称でもない不思議な図形。けれどもこれが柱5本のときの答であることは、線を物差しで測って合計してみれば、これ以外に答がないことがわかる。
ちなみに柱6本のときの正解はわかりやすい。
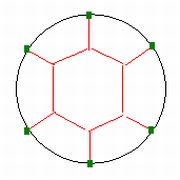
このように石鹸膜の形を不思議ともいえる形に決めている法則はいったいどんなものなのだろうか?
柱3本から6本についての「正解」を見ると、膜をあらわす3つの線が1つの点に集まっているのがわかる。この点のことを「フェルマー点」と呼ぶ。実はフェルマー点に集まる3つの線のなす角度は互いに120度であるという共通点があるのだ。つまりこの点を中心にして3方向に膜は同じ配分で表面張力が分散されているわけだ。
法則のからくりを聞いてしまえば不思議は不思議でなくなるのだが、5という柱の数が見せてくれる非対称な形は、神様のいたずらと僕には思えてしまうのである。
興味がある人は、柱が7本以上の場合も実験したり図を描いたりして答を見つけてみてほしい。
応援クリックをお願いします!




関連リンク:
フェルマー点
http://kikagaku.at-ninja.jp/triangle_geometry/Fermat_point.html
三角形のフェルマー点の3通りの証明
http://mathtrain.jp/fermat
参考ページ:
正方形の頂点を最短距離で結ぶ。(以下のページの中ほどの説明を参照)
http://www.lcv.ne.jp/~hhase/memo/m02_11a.html

自然界には対称的な形をしたものがほとんどだ。太陽や地球も球であるし、惑星の軌道は楕円軌道なので線対称だ。地上に目をうつしても人間をはじめとする動物の体は左右対称だし、電磁波もきれいなサインカーブで線対称だ。ひまわりの花についている種はきれいな螺旋を描いているし、巻貝の美しい模様は回転対称的な自然の美を感じさせてくれる。
対称的なのはなにも「形」だけではない。磁石にはN極とS極があり、電気はプラスとマイナスがある。空間自体も3次元的に対称的だし時間には過去と未来という対称性がある。
神様は自然法則を作るにあたってどうも「対称性」をかなり意識したように思える。
ところが、ときおり神様はいたずらをして対称的でないものを私たちに見せてくれることがある。今日紹介するのはそのような「神様のいたずら」の一例だ。
----------------------
円形の透明なプラスチック板を2枚用意し、間に5ミリほどの空間ができるようにして固定する。プラスチック板の外周に小さな柱を取り付けて固定すればよい。
そのプラスチック円板が十分入るくらいの大きさの洗面器に石鹸水を入れておく。シャボン玉ができるくらいの濃さがよい。
円板の周囲に2本柱を取り付けたものを、石鹸水に沈めて静かに引き上げると柱と柱の間に石鹸水の膜ができる。円板を上から見ると、膜はこの図の赤線で示される。

石鹸膜は表面張力によって面積が最小になろうとするから、上から見た図で膜をあらわす赤い線は2つの柱を結ぶ直線になる。
次に柱の数を3本に増やして同じ実験をしたら石鹸膜はどのような形になるだろうか?このような形になるのだろうか?

残念ながら、こうはならない。3つの柱を結ぶ線の長さを合計したものを最小にするためには、次のような形になるのだ。実験してみるとこのような膜があらわれる。円板の中に柱は立っていないのに石鹸膜をあらわす線は1点に集まってしまうのだ。

さらに柱の数を4本にするとどうだろうか?このような膜があらわれるだろうか?

これも不正解である。柱4本のときは、ちょっと不思議な膜ができるのだ。これが4つの柱を結ぶ膜の長さの合計が最小になる場合の答だ。

柱の数を5本にすると、さらに難しくなる。けれども自然にとっては何がやさしくて何が難しいかは関係ない。与えられた法則にしたがって形を決めるだけなのだから。5本のときはこのような膜があらわれるのだろうか?

実はこれも不正解。柱が5本のときは、次のように不思議な形がでてきてしまうのだ。

点対称でも線対称でもない不思議な図形。けれどもこれが柱5本のときの答であることは、線を物差しで測って合計してみれば、これ以外に答がないことがわかる。
ちなみに柱6本のときの正解はわかりやすい。

このように石鹸膜の形を不思議ともいえる形に決めている法則はいったいどんなものなのだろうか?
柱3本から6本についての「正解」を見ると、膜をあらわす3つの線が1つの点に集まっているのがわかる。この点のことを「フェルマー点」と呼ぶ。実はフェルマー点に集まる3つの線のなす角度は互いに120度であるという共通点があるのだ。つまりこの点を中心にして3方向に膜は同じ配分で表面張力が分散されているわけだ。
法則のからくりを聞いてしまえば不思議は不思議でなくなるのだが、5という柱の数が見せてくれる非対称な形は、神様のいたずらと僕には思えてしまうのである。
興味がある人は、柱が7本以上の場合も実験したり図を描いたりして答を見つけてみてほしい。
応援クリックをお願いします!

関連リンク:
フェルマー点
http://kikagaku.at-ninja.jp/triangle_geometry/Fermat_point.html
三角形のフェルマー点の3通りの証明
http://mathtrain.jp/fermat
参考ページ:
正方形の頂点を最短距離で結ぶ。(以下のページの中ほどの説明を参照)
http://www.lcv.ne.jp/~hhase/memo/m02_11a.html
























