
「世界は2乗でできている 自然にひそむ平方数の不思議:小島寛之」(Kindle版)
内容紹介:
2乗を通して見る、深遠な数学と物理の世界。同じ数を2回掛けると現われる「平方数」には、数の「遊び心」や物理現象の秘密がかくれている。ピタゴラス、ガウス、フェルマー、リーマンら偉大な数学者の業績に見える平方数から、ガリレイ、ボーア、アインシュタインら偉大な物理学者が見いだした自然法則まで、平方数に秘められた不思議で深遠な世界をわかりやすく紹介する。
2013年8月20日刊行、248ページ。
著者について:
小島寛之(こじま ひろゆき): ウィキペディアの記事
1958年、東京生まれ。東京大学理学部数学科卒。同大学院経済学研究科博士課程修了。経済学博士。現在、帝京大学経済学部経済学科教授。数学エッセイストとしても活躍。
小島先生の著書: Amazonで検索
理数系書籍のレビュー記事は本書で458冊目。
数学、特に統計学や経済数学を中心に多くの入門書、副読本をお書きになってきた小島先生による本だ。2013年に講談社ブルーバックスから刊行されて以来、気にはなっていたものの、自分にはやさし過ぎると早合点していたため、読むのが遅くなってしまった。
高校で物理を学んだ人であれば、自然法則に「2乗(平方数)」がよく現れることに気がついていることだろう。万有引力(重力)やクーロン力(静電気力、磁力)は距離の2乗に反比例して減衰するし、光源から発する光の強さ、音源から発する音の強さも距離の2乗に反比例して減衰する。それらはまったく違うものなのに、なぜ同じように減衰していくのか。からくりを理解していないうちは、それを神秘的、不思議に思ったりするものだ。
とどのつまり、それは空間の次元数が縦横高さの3次元だからである。これらの例で共通しているのは、それがエネルギーの拡散であるということだ。エネルギー源から空間的に四方八方に広がるエネルギーは、距離の2乗に反比例して弱まっていく。エネルギー源を頂点とする円錐を考えたとき、距離(=円錐の高さ)が長くなるに従い、円錐の底面積は距離の2乗に比例して大きくなるからだ。したがって、円錐の底面の単位面積が受けるエネルギーは距離の2乗に反比例することになる。
世界には2乗があふれているといっても、しくみを理解できれば何ということはない。本書をタイトルだけで判断して「易しい本」、「当たり前のことが書かれている本」だと僕は早とちりしていた。そうであるにもかかわらず、読もうと思ったのは第8章に「ボーアと水素原子内の平方数」が書かれていることに気がついたからである。
水素原子でバルマー系列、ライマン系列、パッシェン系列として知られる発光スペクトルのパターンに平方数(数式上では平方数の逆数)が現れるのはなぜなのか、僕はど忘れしていた。
水素原子模型と波動方程式: PDF資料Web閲覧
それ以外にも面白いと感じたことが本書にはたくさん見つかった。本書で取り上げられているのは「数学に現れる2乗」と「物理法則に現れる2乗」に分かれているが、僕が神秘的に感じたのは数学、特に「数論に現れる2乗」だった。要するに自分よく理解できていない世界、学習不足の領域に見られる「2乗」に心惹かれたのだと思う。
何を面白く感じるか、神秘的に感じるかは、その人の知識や理解、学習進度に大きく左右されるものだ。全人類が理解に達していないとき、私たちはそれを神秘と呼んでいる。
本書では9つの例を取り上げて解説している。ひとつずつ解説や感想を簡潔に書いておこう。
第1章:ピタゴラスの定理
ピタゴラスの定理の2乗が現れるのは当たり前だが、この定理を侮ってはならない。この定理は、数学の発展に大きく分けて3つの貢献をしている。第一は数論への貢献であり、第二は無理数論への貢献、そして第三には幾何学的な計量理論への貢献である。本書ではこの章のほか、この3つの貢献を別の章で詳しく解説している。ピタゴラスの定理の大切さを教えてくれる。
第2章:フィボナッチと合同数
理系ファンなら誰でも知っているフィボナッチ数。この数列にまつわる話と2乗(平方数)が結び付けられことは知らなかった。興味深く読むことができた。
第3章:ガリレイと落体運動
この章の内容は知っていたので、特に面白いとは感じなかった。要するに運動エネルギーが速度の2乗に比例するということ、高校の力学の範囲が理解できれいればわかる話である。
第4章:フェルマーと4平方数定理
興味深く読むことができた。それはフェルマーの小定理、大定理は知っていたが、フェルマーの2平方数定理、4平方数定理を僕が知らなかったからだと思う。
第5章:ガウスと虚数
興味深く読むことができた。フェルマーの2平方数定理をガウスが虚数を使って再証明したあたり、ガウス整数の話がよい。
第6章:オイラーとリーマン
この章がいちばん興味深く読むことができた。「平方数の逆数をすべて足すといくつになるか」という「バーゼル問題」は、1644年に ピエトロ・メンゴリによって提起され、1735年にレオンハルト・オイラーによって解かれた有名な問題である。バーゼル問題はその後、ゼータ関数(ζ関数)の発見、素数の研究を飛躍的に発展させることにつながった。平方数の逆数和がなぜ素数と密接に関係しているのか?その数式を導出できたとしてもても、あなたはその理由や意味を述べることができるだろうか。(解説)
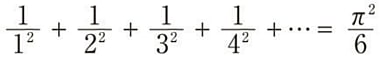
そして、ミクロの物質の世界では「カシミール効果」という物理現象を場の量子論で解析するときに ζ(-3) = 1/120 が本質的な役割を果たしている。
この2つの例は神秘的としか言いようがない。

ζ(-3) = 1/120 : WolframAlphaで計算してみる 解説
第7章:ピアソンとカイ2乗分布
興味深く読めた。それは標準偏差や正規分布に2乗が現れるからくりは理解していたが、その先のピアソンやカイ2乗分布の話は知らなかったからである。あと、ガウスの誤差理論、最小二乗法に2乗がでてくるからくりも「なるほど!」という感じで読むことができた。
第8章:ボーアと水素原子内の平方数
本書を読むきっかけとなった章である。スペクトルの系列の数式に平方数の逆数がでてくるのは、要するに電子の運動エネルギー(速度の2乗)が本質的な役割を果たしているからだと理解した。
第9章:アインシュタインとE=mc^2
この章の内容は知っていた。特殊相対性理論は4次元の幾何学であり、本質的には4次元のピタゴラスの定理のようなものである。E=mc^2という式の導き方を知っていれば、この式に2乗がでてくることは容易に理解できる。
多くの方に読んでいいただきたい本だ。しかし、数式を引用して説明している。微積分の知識は不要だが、高校の数学II+B程度まで理解していることが読者の前提条件だ。




「世界は2乗でできている 自然にひそむ平方数の不思議:小島寛之」(Kindle版)

はじめに
第1章:ピタゴラスの定理
- 平方数の楽しみ
- 2乗についての大事な公式
- 平方といえばピタゴラス
- ピタゴラス数
- 無理数の発見
- 無理数の難しさ
- 空間の計測
[平方数を好きになる問題]1
第2章:フィボナッチと合同数
- フィボナッチ数
- フィボナッチ数と平方数
- 数学試合
- 合同数の問題
- ペル方程式
- 双曲線上に解が並ぶ
- 無理数との関係
- ペル方程式の解法
- ペル方程式のその後の展開
[平方数を好きになる問題]2
第3章:ガリレイと落体運動
- ガリレイの実験
- 慣性の法則
- 運動エネルギーは速度の2乗
- ケプラーの法則
- ニュートンの万有引力
- 月が地球に落ちてこない理由
- 円運動の加速度を求める
[平方数を好きになる問題]3
第4章:フェルマーと4平方数定理
- 数論の祖フェルマー
- フェルマーの小定理
- フェルマーの大定理
- 2平方数定理
- 4平方数定理
- 母関数による別証明
- 4平方数定理の母関数による証明
- 10進法と2進法
- p進数とは何か
- 7で割り切れるほど近くなる
- 7進数の中での2の平方根
- 4平方数定理とp進数
[平方数を好きになる問題]4
第5章:ガウスと虚数
- 天才ガウス
- 合同式
- 平方剰余の研究
- 2平方数定理と虚数
- ガウス整数
- 2平方数定理ふたたび
- 類体論という壮大な世界
[平方数を好きになる問題]5
第6章:オイラーとリーマン
- 平方数の逆数をすべて足すといくつになるか?
- 18世紀最大の数学者オイラー
- 無限の和
- 関数を無限次の多項式で表す
- 三角関数を無限次の多項式で表す
- 解と係数の関係を復習しよう
- 円周率の平方がなぜ現れるのか
- 平方数の逆数和が素数と関係する!
- オイラー積はなぜ成り立つのか
- リーマンのゼータ関数
- 短命の数学者リーマン
- 史上最大の難問リーマン予想
- ミクロの物質の物理学にゼータが現れた!
[平方数を好きになる問題]6
第7章:ピアソンとカイ2乗分布
- 今や、データ解析は必須
- 散らばりを代表する標準偏差
- 標準偏差は2乗平均
- 正規分布の発見
- 一般の正規分布
- この世界には正規分布がいっぱい
- ガウスの誤差理論
- 統計学者ピアソン
- カイ2乗分布の発見
- ピアソンの適合度検定
- ピアソン vs フィッシャー
[平方数を好きになる問題]7
第8章:ボーアと水素原子内の平方数
- プリズムと虹
- 水素のスペクトルはなぜか飛び飛び
- 平方数が出現
- 現代物理学の父ニールス・ボーア
- 原子の中の宇宙法則
- 量子跳躍と量子条件
- 電子の軌道が飛び飛びなのはなぜか
- 幸運な偶然
- ミクロの世界は複素数の姿をしている
- 幸運な一致の理由
[平方数を好きになる問題]8
第9章:アインシュタインとE=mc^2
- 天才アインシュタインの特殊相対性理論
- 川の流れの速度を知る方法
- 動く世界の速度を求める
- 音波を利用すれば船の速度がわかる
- 地球の絶対速度を求める試み
- 空間は収縮する
- いよいよ、アインシュタインの登場
- 歪む時間
- 異なる座標系の観測者
- 歪む時間・空間の中での不変量
- E=mc^2の発見
[平方数を好きになる問題]9
内容紹介:
2乗を通して見る、深遠な数学と物理の世界。同じ数を2回掛けると現われる「平方数」には、数の「遊び心」や物理現象の秘密がかくれている。ピタゴラス、ガウス、フェルマー、リーマンら偉大な数学者の業績に見える平方数から、ガリレイ、ボーア、アインシュタインら偉大な物理学者が見いだした自然法則まで、平方数に秘められた不思議で深遠な世界をわかりやすく紹介する。
2013年8月20日刊行、248ページ。
著者について:
小島寛之(こじま ひろゆき): ウィキペディアの記事
1958年、東京生まれ。東京大学理学部数学科卒。同大学院経済学研究科博士課程修了。経済学博士。現在、帝京大学経済学部経済学科教授。数学エッセイストとしても活躍。
小島先生の著書: Amazonで検索
理数系書籍のレビュー記事は本書で458冊目。
数学、特に統計学や経済数学を中心に多くの入門書、副読本をお書きになってきた小島先生による本だ。2013年に講談社ブルーバックスから刊行されて以来、気にはなっていたものの、自分にはやさし過ぎると早合点していたため、読むのが遅くなってしまった。
高校で物理を学んだ人であれば、自然法則に「2乗(平方数)」がよく現れることに気がついていることだろう。万有引力(重力)やクーロン力(静電気力、磁力)は距離の2乗に反比例して減衰するし、光源から発する光の強さ、音源から発する音の強さも距離の2乗に反比例して減衰する。それらはまったく違うものなのに、なぜ同じように減衰していくのか。からくりを理解していないうちは、それを神秘的、不思議に思ったりするものだ。
とどのつまり、それは空間の次元数が縦横高さの3次元だからである。これらの例で共通しているのは、それがエネルギーの拡散であるということだ。エネルギー源から空間的に四方八方に広がるエネルギーは、距離の2乗に反比例して弱まっていく。エネルギー源を頂点とする円錐を考えたとき、距離(=円錐の高さ)が長くなるに従い、円錐の底面積は距離の2乗に比例して大きくなるからだ。したがって、円錐の底面の単位面積が受けるエネルギーは距離の2乗に反比例することになる。
世界には2乗があふれているといっても、しくみを理解できれば何ということはない。本書をタイトルだけで判断して「易しい本」、「当たり前のことが書かれている本」だと僕は早とちりしていた。そうであるにもかかわらず、読もうと思ったのは第8章に「ボーアと水素原子内の平方数」が書かれていることに気がついたからである。
水素原子でバルマー系列、ライマン系列、パッシェン系列として知られる発光スペクトルのパターンに平方数(数式上では平方数の逆数)が現れるのはなぜなのか、僕はど忘れしていた。
水素原子模型と波動方程式: PDF資料Web閲覧
それ以外にも面白いと感じたことが本書にはたくさん見つかった。本書で取り上げられているのは「数学に現れる2乗」と「物理法則に現れる2乗」に分かれているが、僕が神秘的に感じたのは数学、特に「数論に現れる2乗」だった。要するに自分よく理解できていない世界、学習不足の領域に見られる「2乗」に心惹かれたのだと思う。
何を面白く感じるか、神秘的に感じるかは、その人の知識や理解、学習進度に大きく左右されるものだ。全人類が理解に達していないとき、私たちはそれを神秘と呼んでいる。
本書では9つの例を取り上げて解説している。ひとつずつ解説や感想を簡潔に書いておこう。
第1章:ピタゴラスの定理
ピタゴラスの定理の2乗が現れるのは当たり前だが、この定理を侮ってはならない。この定理は、数学の発展に大きく分けて3つの貢献をしている。第一は数論への貢献であり、第二は無理数論への貢献、そして第三には幾何学的な計量理論への貢献である。本書ではこの章のほか、この3つの貢献を別の章で詳しく解説している。ピタゴラスの定理の大切さを教えてくれる。
第2章:フィボナッチと合同数
理系ファンなら誰でも知っているフィボナッチ数。この数列にまつわる話と2乗(平方数)が結び付けられことは知らなかった。興味深く読むことができた。
第3章:ガリレイと落体運動
この章の内容は知っていたので、特に面白いとは感じなかった。要するに運動エネルギーが速度の2乗に比例するということ、高校の力学の範囲が理解できれいればわかる話である。
第4章:フェルマーと4平方数定理
興味深く読むことができた。それはフェルマーの小定理、大定理は知っていたが、フェルマーの2平方数定理、4平方数定理を僕が知らなかったからだと思う。
第5章:ガウスと虚数
興味深く読むことができた。フェルマーの2平方数定理をガウスが虚数を使って再証明したあたり、ガウス整数の話がよい。
第6章:オイラーとリーマン
この章がいちばん興味深く読むことができた。「平方数の逆数をすべて足すといくつになるか」という「バーゼル問題」は、1644年に ピエトロ・メンゴリによって提起され、1735年にレオンハルト・オイラーによって解かれた有名な問題である。バーゼル問題はその後、ゼータ関数(ζ関数)の発見、素数の研究を飛躍的に発展させることにつながった。平方数の逆数和がなぜ素数と密接に関係しているのか?その数式を導出できたとしてもても、あなたはその理由や意味を述べることができるだろうか。(解説)
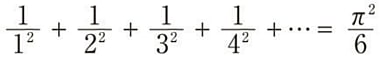
そして、ミクロの物質の世界では「カシミール効果」という物理現象を場の量子論で解析するときに ζ(-3) = 1/120 が本質的な役割を果たしている。
この2つの例は神秘的としか言いようがない。

ζ(-3) = 1/120 : WolframAlphaで計算してみる 解説
第7章:ピアソンとカイ2乗分布
興味深く読めた。それは標準偏差や正規分布に2乗が現れるからくりは理解していたが、その先のピアソンやカイ2乗分布の話は知らなかったからである。あと、ガウスの誤差理論、最小二乗法に2乗がでてくるからくりも「なるほど!」という感じで読むことができた。
第8章:ボーアと水素原子内の平方数
本書を読むきっかけとなった章である。スペクトルの系列の数式に平方数の逆数がでてくるのは、要するに電子の運動エネルギー(速度の2乗)が本質的な役割を果たしているからだと理解した。
第9章:アインシュタインとE=mc^2
この章の内容は知っていた。特殊相対性理論は4次元の幾何学であり、本質的には4次元のピタゴラスの定理のようなものである。E=mc^2という式の導き方を知っていれば、この式に2乗がでてくることは容易に理解できる。
多くの方に読んでいいただきたい本だ。しかし、数式を引用して説明している。微積分の知識は不要だが、高校の数学II+B程度まで理解していることが読者の前提条件だ。




「世界は2乗でできている 自然にひそむ平方数の不思議:小島寛之」(Kindle版)

はじめに
第1章:ピタゴラスの定理
- 平方数の楽しみ
- 2乗についての大事な公式
- 平方といえばピタゴラス
- ピタゴラス数
- 無理数の発見
- 無理数の難しさ
- 空間の計測
[平方数を好きになる問題]1
第2章:フィボナッチと合同数
- フィボナッチ数
- フィボナッチ数と平方数
- 数学試合
- 合同数の問題
- ペル方程式
- 双曲線上に解が並ぶ
- 無理数との関係
- ペル方程式の解法
- ペル方程式のその後の展開
[平方数を好きになる問題]2
第3章:ガリレイと落体運動
- ガリレイの実験
- 慣性の法則
- 運動エネルギーは速度の2乗
- ケプラーの法則
- ニュートンの万有引力
- 月が地球に落ちてこない理由
- 円運動の加速度を求める
[平方数を好きになる問題]3
第4章:フェルマーと4平方数定理
- 数論の祖フェルマー
- フェルマーの小定理
- フェルマーの大定理
- 2平方数定理
- 4平方数定理
- 母関数による別証明
- 4平方数定理の母関数による証明
- 10進法と2進法
- p進数とは何か
- 7で割り切れるほど近くなる
- 7進数の中での2の平方根
- 4平方数定理とp進数
[平方数を好きになる問題]4
第5章:ガウスと虚数
- 天才ガウス
- 合同式
- 平方剰余の研究
- 2平方数定理と虚数
- ガウス整数
- 2平方数定理ふたたび
- 類体論という壮大な世界
[平方数を好きになる問題]5
第6章:オイラーとリーマン
- 平方数の逆数をすべて足すといくつになるか?
- 18世紀最大の数学者オイラー
- 無限の和
- 関数を無限次の多項式で表す
- 三角関数を無限次の多項式で表す
- 解と係数の関係を復習しよう
- 円周率の平方がなぜ現れるのか
- 平方数の逆数和が素数と関係する!
- オイラー積はなぜ成り立つのか
- リーマンのゼータ関数
- 短命の数学者リーマン
- 史上最大の難問リーマン予想
- ミクロの物質の物理学にゼータが現れた!
[平方数を好きになる問題]6
第7章:ピアソンとカイ2乗分布
- 今や、データ解析は必須
- 散らばりを代表する標準偏差
- 標準偏差は2乗平均
- 正規分布の発見
- 一般の正規分布
- この世界には正規分布がいっぱい
- ガウスの誤差理論
- 統計学者ピアソン
- カイ2乗分布の発見
- ピアソンの適合度検定
- ピアソン vs フィッシャー
[平方数を好きになる問題]7
第8章:ボーアと水素原子内の平方数
- プリズムと虹
- 水素のスペクトルはなぜか飛び飛び
- 平方数が出現
- 現代物理学の父ニールス・ボーア
- 原子の中の宇宙法則
- 量子跳躍と量子条件
- 電子の軌道が飛び飛びなのはなぜか
- 幸運な偶然
- ミクロの世界は複素数の姿をしている
- 幸運な一致の理由
[平方数を好きになる問題]8
第9章:アインシュタインとE=mc^2
- 天才アインシュタインの特殊相対性理論
- 川の流れの速度を知る方法
- 動く世界の速度を求める
- 音波を利用すれば船の速度がわかる
- 地球の絶対速度を求める試み
- 空間は収縮する
- いよいよ、アインシュタインの登場
- 歪む時間
- 異なる座標系の観測者
- 歪む時間・空間の中での不変量
- E=mc^2の発見
[平方数を好きになる問題]9























ご無沙汰していますが今年は80歳の大台に乗りました。コロナ禍にも負けず元気にしています。
お久しぶりです。
記事本文に書いたように、タイトルから想像されるよりずっと面白い本ですた。
ついに80代になられましたか。ワクチンはもう1回目を接種されたと思いますが、コロナはなかなかしぶといですね。おそらくワクチンが国民の大半に接種される来年あたりにはおさまっていることを願っています。