Cube root 721,734,273 using abacus (Triple-root method 8)

[Set 721,734,273 on Mr. Cube root]

Zoom

[Japanese]

Today's example is also about actual solution of Cube root using abacus. The calculation becomes more complicated than previous example.

Today's example is simple - basic Triple-root method, root is 3-digits case and requires 9 as root in the middle of calculation. Please check the Theory page for your reference.

Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.


Abacus steps to solve Cube root of 721,734,273
(Answer is 897)

"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.

721,734,273 -> (721|734|273): 721 is the 1st group number. The root digits is 3.


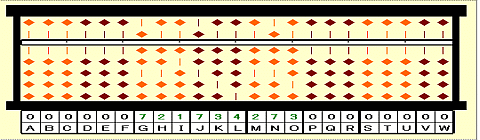
Step 1: Set 721734273. First group is 721.


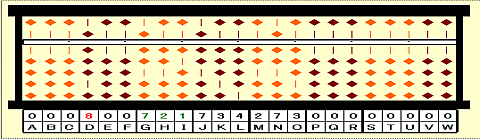
Step 2: Cube number smaller than 721 is 512=8^3. Place 8 on D as 1st root.


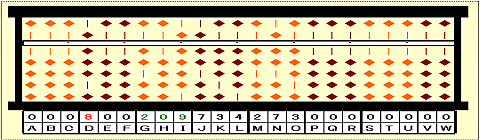
Step 3: Place 721-512=209 on GHI.(-a^3)


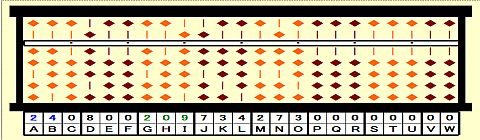
Step 4: Place Triple root 3x8=24 on AB.


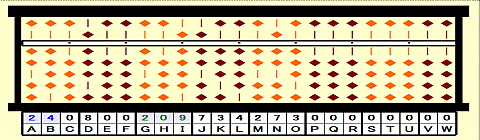
Step 5: Repeat division by triple root 24 until 4th digits next to 1st root.(/3a)


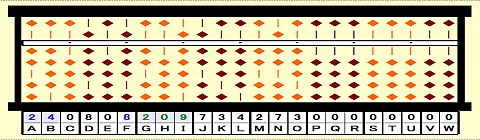
Step 6: 209/24=8 remainder 17. Place 8 on F.


Step 7: Place remainder 017 on GHI.


Step 8: 117/24=7 remainder 9.


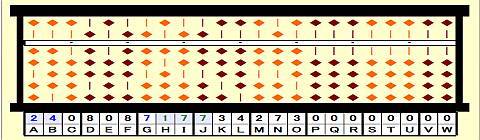
Step 9: Place 7 on G.


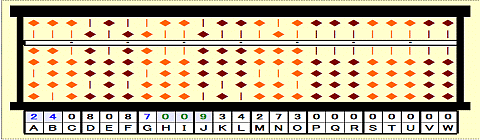
Step 10: Place remainder 009 on HIJ.


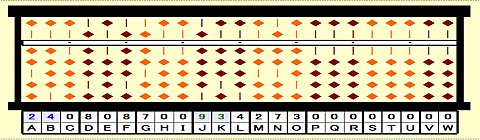
Step 11: 93/24=3 remainder 21.


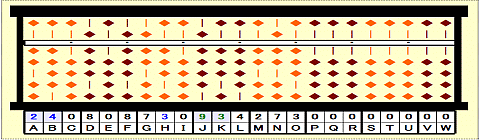
Step 12: Place 3 on H.


Step 13: Place remainder 21 on JK.


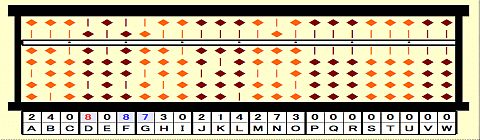
Step 14: Divide 87 on FG by current root 8. 87/8=10 remainder 7.


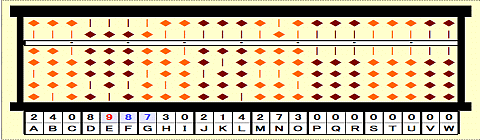
Step 15: Place 9 as 2nd root on E according to the calculation rule.


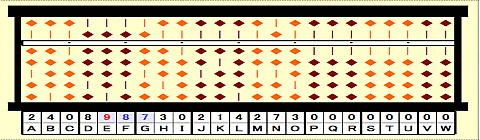
Step 16: Divide 87 on FG by 2nd root 9. 87/9=8 remainder 15.


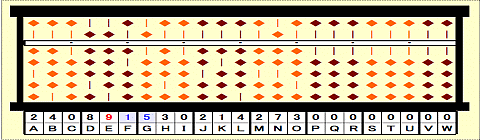
Step 17: Place remainder 15 on FG.


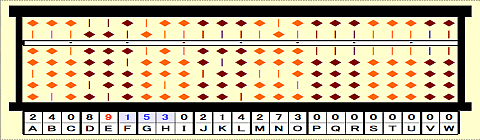
Step 18: Subtract 2nd root^2 from 153 on FGH. (-b^2)


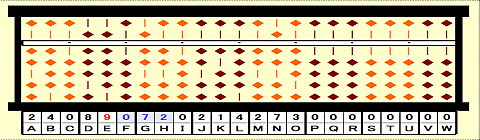
Step 19: Place 153-9^2=072 on FGH.


Step 20: Multiply triple root 24 by remainder 72 on GH. 24X72=1728


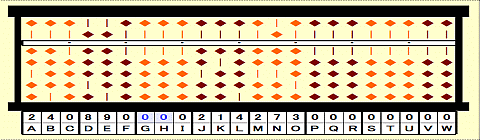
Step 21: Replace 72 by 00 on GH.


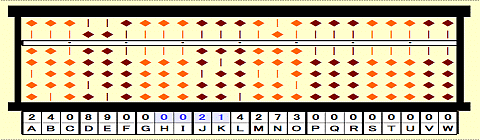
Step 22: Add 1728 to 0021 on HIJK.


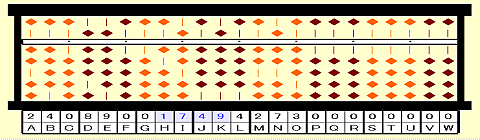
Step 23: It means place 0021+1728=1749 on HIJK.


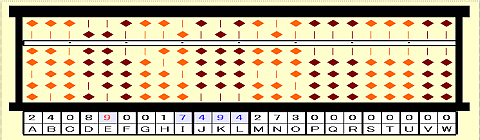
Step 24: Subtract 2nd root^3 from 7494 on IJKL. (-b^3)


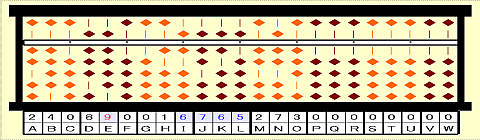
Step 25: It means place 7494-9^3=6765 on IJKL.


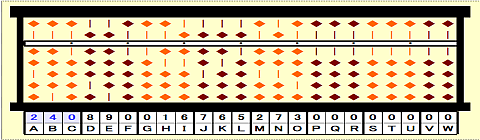
Step 26: Focus on triple root (ABC).


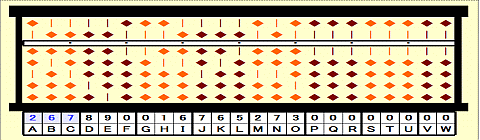
Step 27: Add 3x2nd root to triple root root on BC. Place 240+3x9=267 on ABC.


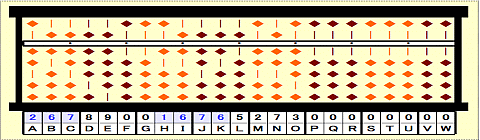
Step 28: Repeat division by triple root 267 until fixed position. (/3a)


Step 29: Divide 1676 on HIJK by triple root 267. Place 1676/267=6 remainder 74. Place 6 on G.


Step 30: Place 0074 on HIJK.


Step 31: 745/267=2 remainder 211


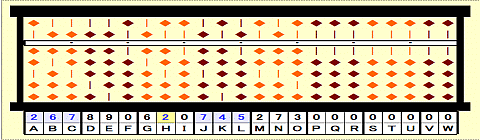
Step 32: Place 2 on H.


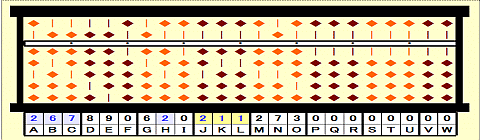
Step 33: Place remainder 211 on JKL.


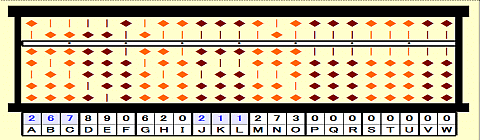
Step 34: 211/267=7 remainder 24


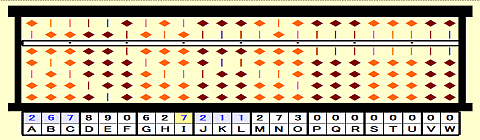
Step 35: Place 7 on I.


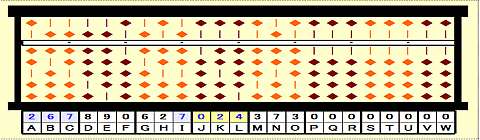
Step 36: Place remainder 024 on JKL.


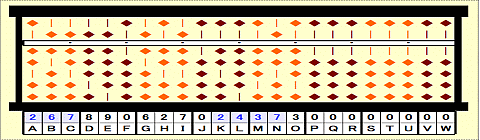
Step 37: 2437/267=9 remainder 34


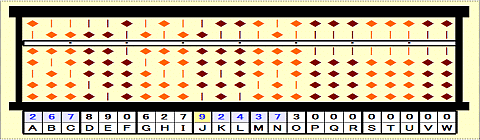
Step 38: Place 9 on J.


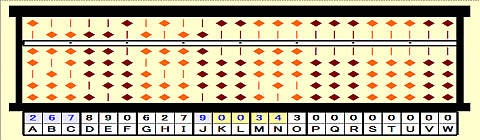
Step 39: Place remainder 0034 on KLMN.


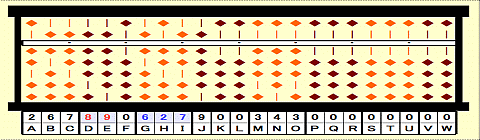
Step 40: Divide 627 by current root 89.


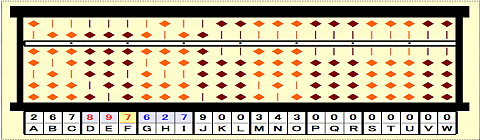
Step 41: 627/89=7 remainder 4. Place 7 on F as 3rd root.


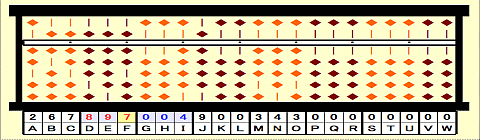
Step 42: Place remainder 004 on GHI.


Step 43: Subtract 3rd root^2 from 49 on IJ. (-c^2)


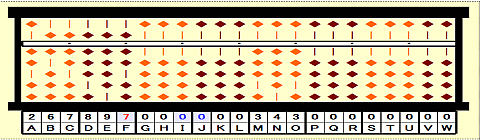
Step 44: Place 49-7^2=00 on IJ.


Step 45: Subtract 3rd root^3 from 343 on MNO. (-c^3)


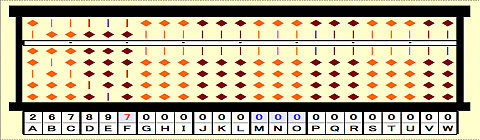
Step 46: Place 343-7^3=000 on MNO.


Step 47: Cube root of 721734273 is 897.


Final state: Answer 897

Abacus state transition. (Click to Zoom)




Next article is also about Cube root calculation (Triple-root method).


Related articles:

How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed

Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b


Please place your mouse on the buttons and click one by one. These are blog ranking sites.