
「熱の解析的理論:ジョゼフ・フーリエ著、ガストン・ダルブー編纂」(電子書籍)
内容(「BOOK」データベースより)
本書は、ジョゼフ・フーリエ(1768-1830)の原書をおよそ70年後に数学者ガストン・ダルブー(1842-1917)が編纂したものを訳したものである。全文9章663頁からなる。熱伝導の方程式は第2章、フーリエ展開公式は第3章、方程式の解は第4-9章で紹介する。
翻訳者:竹下 貞雄 (たけした さだお)
1933年 福井市に生まれる。
1958年 京都大学卒業
1958年 日本国有鉄道入社
1964年 ベルギーのリェージュ大学留学(1年)
1983年 鉄道技術研究所,土質研究室長
1985年 工学博士(京都大学)
1986年 立命館大学理工学部教授
2009年 同上退職。
現在は翻訳業に従事している。
理数系書籍のレビュー記事は本書で211冊目。(直前の記事までに紹介した大村平先生の著書4冊は大学受験前に読んだ本なのでカウントには含めないことにした。)
今回は歴史的な名著を読んでみた。先月「高校数学でわかるフーリエ変換:竹内淳」を紹介したのは本書を念頭においてのことだったのである。
科学史上の名著のひとつ
フランスの数学者、物理学者のジョゼフ・フーリエ(1768-1830)が1822年に著した「Theorie analytique de la chaleur」という本の日本語訳だ。(正確に言えば数学者ガストン・ダルブー(1842-1917)が編纂した1890年刊行本の日本語訳である。)これは19世紀でもっとも重要な書物のひとつと言われている。
フーリエはこの中でフーリエ級数やフーリエ変換の方法をはじめて紹介し、これを使って固体の熱伝導現象を表す偏微分方程式を解析的に解いた。この本は数理科学、応用数学上きわめて重要な意味を持っている。


1822年の初版本は金沢工業大学ライブラリーセンターに所蔵されていて、次のページで説明を読むことができる。
ジャン・バティスト・ジョゼフ・フーリエ (1768-1839) 熱の解析的理論 パリ, 1822年初版
http://www.kanazawa-it.ac.jp/dawn/182201.html
フランス語版の著作権はとっくの昔に切れているので、ネット上では現在次の2つの版を読むことができる。(PDFファイルとしてダウンロードも可)
1822年刊行、フーリエ著のオリジナル(見てみる)
1883年刊行、フーリエ著、バロン版(見てみる)- バロン(baron)とは「男爵」の意味。
Archive.org: フランス語版を検索
理数系の外国語の文章は文学のように難解ではないので、フランス語の原典は仏検2級レベルの読解力と理数系大学1、2年レベルの数学力があればなんとか読めると思う。
フランス語版や英語版の書籍はそれぞれの国のアマゾンから購入できる。いろいろな版がでているのでお求めになるときは注意したほうがよい。ダルブー編纂の本は偏微分方程式に現代と同じ「∂」記号が使われているが、フーリエ(オリジナル)やバロンの本は「∂」のかわりに「d」が使われているからだ。(今回紹介した日本語版はダルブー編纂の翻訳なので「∂」を使っている。)
フランス語版:Theorie Analytique De La Chaleur:Amazon.co.jpで検索
英語版:The Analytical Theory Of Heat:Amazon.comで検索、Amazon.co.jpで検索
竹下先生が翻訳を始めた2004年頃はフランス語版、英語版共に入手が極めて困難だったことが「訳者あとがき」に書かれているが、幸い両言語共に近年になって発売されたことになる。
日本語版について
日本語版「熱の解析的理論:ジョゼフ・フーリエ著、ガストン・ダルブー編纂」を翻訳されたのは竹内貞雄先生。現在「ラプラスの天体力学論 全5巻」を翻訳されている。
「熱の解析的理論」が日本語版として刊行されたのは2005年のことである。「訳者あとがき」によると翻訳はフーリエの原書(1822)を用いたが、説明文の中に数式が入っていることが多く、現在のテキストとは違和感があるので途中からダルブー編纂(1890)のものを使ったそうだ。本は科学雑誌Newtonと同じ大判のB5サイズで、340ページ。読み応えは十分ある。数学的な記述レベルは理数系大学1、2年で足りるが、読み通すのにはかなりの忍耐が要求される。
「熱の解析的理論」はその後、紙の本は絶版になり電子書籍が発売された。またフランス語原典に関しては、以下の種類のものが無料で公開されている。
1. 大学教育出版(電子書籍):開く
2. 1822原著:開く
3. Darboux編・Fourier全集t.1:開く
4. (参考)Fourier全集t.2(完):開く
5. reprint (Gabay):開く
本書を読んだ理由
このタイミングで僕がこの本を読んだのには、次のような理由が重なっていたからだ。
- 今年に入ってから物理学科で学ぶ熱力学の本を集中的に読んでいる。もっと遡れば「ファインマン計算機科学」を読んで情報エントロピーと熱力学エントロピーの関連性を知ったことに端を発している。熱力学のメインは第1、第2、第3法則だ。けれどもこの中には時間変数 t があらわれない。時間変数 t を使う熱の理論というのは熱伝導や伝熱学のことだ。これらについても学びたいと思ったから。
- 本書を翻訳された竹内貞雄先生による「ラプラスの天体力学論」の第5巻が今月末に発売され、全5巻が揃う予定。先生の著作(翻訳)を紹介するにはよいタイミングであること。そして、この記事が竹内先生のお目にとまるかどうかはわからないが、翻訳された本を真面目に読んだ人がここに一人いることを示しておきたいという気持ちもある。
- フーリエの人生はおよそ200年前のフランス革命やナポレオンの時代と重なっている。当時の解析学のレベルを実感してみたいと思ったこと。
- フーリエ級数やフーリエ変換と熱伝導の関係をしっかり理解したいと思ったこと。これは現代の教科書でもよいわけだが、発想や思考過程を追うためにはやはり最初に理論を開拓したご本人の著作を読むのがいちばんだと思ったから。
- コンピュータによる数値計算を使わない解析的手法(数式だけの計算)で、熱伝導をどこまで記述でき、解を得られるかということに関心があったから。
- 基礎となる原理は「フーリエの法則」というごくシンプルなものだが、熱伝導の対象となる物の形が違うと、偏微分方程式で表される熱の運動方程式やその解き方がどれくらい違ってくるのかということに関心があったため。
フーリエの法則:物体を通過する伝熱速度は、熱の流れに垂直な断面積(伝熱面積)に比例し、流れの方向に沿った温度勾配の符号を変えたものに比例する。単位伝熱面積当たりにすると 熱流束密度 J=-λ(dT/dx)と書ける。
これだけの理由があったから僕はどうしてもこの本が読みたかった。日本語版の新品本は売切れていたので値段の高い中古本しか手に入らない。アマゾンの画面をにらみながら「うーむ、どうしよう。。。」と悩む間もなく購入ボタンをクリックしたのだった。
フーリエにとって「熱」とは?
フーリエがこの本を出したのは1822年。「熱学思想の史的展開:山本義隆」の第3巻に書いたように熱がエネルギーのひとつの形態であることがわかったのは1850年以降のことだ。フーリエの時代は同書でいえば第2巻の前半、ラヴォアジエの「熱素説」やラプラスの「熱量学」が受け入れられていた時代で、フーリエの考えもこれに近かった。そして当時は絶対温度の概念も生まれていなかった。水の凝固点と沸点を基準にその間を等分する目盛を温度計に採用していたから測定値は不正確だったわけだ。
彼が物質としての熱素を信じていたかどうかは本書には書かれていないが、熱は物体の中を移動し、その総量は変わらないから「熱流体」のように取り扱うことができるということは述べられていた。50年後に熱力学第一法則が導かれ、熱は仕事に転換できるエネルギーの一種であることがわかるので、「熱流体」や「熱流束」として計算しても結果が正しいことは後に確認されることになる。
本書がメインテーマとする「熱伝導」とは、固体の中や表面を熱が移動することであり、ざっくばらんな言い方をすれば物体の中を「熱がジワジワと伝わる現象」のことだ。対流や放射など熱伝導以外の方法で熱が伝わることを認識していたことをフーリエは本書で述べている。
フーリエは物質を構成する「分子」についても言及し、その中を熱が伝わると説明している。ただし彼の言うところの分子とはニュートン力学の流れをくむラプラス流、純粋に力学的なもので、物質を構成する粒子として遠距離では万有引力の法則に従い、それらが接するほど近距離では斥力を及ぼし合うという説だった。その数理的なメカニズムは確立されていない。熱流体はそのような分子の中を透過的にすり抜けて伝わっていくと考えたのだ。
物体の比熱や物体の中の熱伝導率、表面から外に出るときの熱伝導率については、物質それぞれについて測定値としてすでに得られていて、フーリエはその結果を熱伝導方程式に取り入れている。
現代における熱伝導の解釈
原子や分子の構造や力学が詳しく解明された現代において熱伝導は原子の「格子振動の伝達と伝導電子の移動」として理解されている。ウィキペディアの「熱伝導の項」では次のように説明されている。
熱伝導:物質の移動を伴わずに高温側から低温側へ熱が伝わる移動現象のひとつである。熱伝導は、フォノン及び伝導電子が担う。特に、金属においては、伝導電子が熱伝導の主要な担い手である。通常の物質では伝導電子による寄与の方が大きいので、金属は半導体や絶縁体(フォノンが主要な熱伝導の担い手)よりも熱伝導性が良い。しかし、非常に硬いダイヤモンドではフォノン(格子振動)を介した熱伝導性の寄与の方が非常に大きくなる。
イメージとしてはこのようなもの。左が伝導電子の移動、右が格子振動だ。

格子振動を量子化したものが「フォノン(音響子)」と呼ばれる準粒子で、音響フォノンと光子フォノンの2種類がある。このうち音響フォノンが熱伝導にたずさわっている。(ウィキペディアの「フォノンの項」を参照)
詳しく知りたい方は、次のようなページをお読みになるとよい。
熱が伝わるとは?
http://okwave.jp/qa/q384684.html
音響フォノンは熱を運んで光学フォノンが熱を運ばない理由
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1395015953
カーボンナノチューブの熱伝導シミュレーション(PDF)
http://www.jim.or.jp/journal/j/pdf3/73/08/583.pdf
伝熱学で使われる用語の説明
現代では熱伝導は伝熱学、伝熱工学の中の一分野として分類されている。伝熱工学は熱の輸送方法の違いによって大まかに次の内容から構成されている。
1)熱伝導(Heat Conduction) =伝導伝熱(Conductive Heat Transfer)
2)対流熱伝達(Convective Heat Transfer)
3)輻射伝熱(Radiative Heat Transfer)、 熱輻射=熱放射(Thermal Radiation)
4)相変化を伴う伝熱(Heat Transfer with Phase Change)
5)熱拡散(Heat Diffsion):固体の場合、物質の拡散に伴う場合
日本語について言えば「伝熱」はいちばん大きなくくりで、固体のときは「伝導」や「伝播」、液体や気体の対流の場合は「伝達」のように使い分けられている。
本書の第8章までは「熱伝導」を取り扱い総和記号Σを使ったフーリエ級数を使う理論、第9章は「熱拡散」を取り扱い積分記号∫を使ったフーリエ変換の理論である。
本書の内容詳細
前置きが長くなったが、章立てに沿って本書の内容を紹介しよう。目次の詳細はこの記事のいちばん下を参照していただきたい。
編者まえがき
編者ダルブーによってフーリエの業績が紹介される。フランスの数学者ダルブーが生まれたのはフーリエの死後12年経った1842年のことである。「まえがき」の中でダルブーはフーリエの熱の理論の研究が1807年の論文要約および1811年の論文が元になっていることや、1822年に「熱の解析的理論」が本として出版されるまでの経緯を説明している。
序論
フーリエ自身による解説はここからはじまる。序論では次のことが述べられている。
- 熱の研究はきわめて大切だが、まだ解明されていない。
- 熱の研究、科学の歴史はアルキメデス以前まで遡ることができる。
- ニュートン力学の普遍性、適用範囲がきわめて広いこと。
- ニュートン力学では熱の挙動を説明できないこと。
- 熱の挙動は少数の事実で説明できること。
- 熱の影響は地球や太陽、大陸や海、気象全般におよび、その研究は物理学や経済に多大な利益をもたらすこと。
- 熱伝導は微分方程式によって解析的に解けること。本書がそれを解説するものであること。
- それまでにフーリエがフランスの科学アカデミーに提出した論文やその評価について。
- 熱の測定結果は数学に結び付けられ進歩していくものであること。
第1章:総論
経験的事実を論理的に積み重ねる形で、「フーリエの法則」が成り立つことを導いている。そのかなめとなるのは物質内の「熱の移動」という現象が温度の高い場所から低い場所に向かう方向で発生し、「重ね合わせ」ができるという事実にある。(線形性が成り立つ。)
この記事ではジョゼフ・フーリエに敬意を払い、フランス語の原書から該当箇所を切り出す形で紹介しよう。
フーリエの法則は、次のように表記されている。本書では全体を通じて温度に対して v や w という変数が使われている。

また、この章では熱の運動には時々刻々変化する「非定常熱伝導」と時間が経過して熱平衡状態に達している「定常熱伝導」があることが解説されている。
そしてこの章では測定値として求められる外的伝導率 H や内的伝導率 K が導入される。外的伝導率は物体の表面から内部に流れ出す熱の伝導率で、内的伝導率は物体の内部で移動する熱の伝導率のことだ。(注意:伝熱学では外的伝導率のことは「熱伝達率」という用語が使われている。)
第2章:熱の運動方程式
前章の結果を利用しながら、この章では熱伝導が行われる物体で成り立っている熱の運動方程式が偏微分方程式の形で紹介される。式は物体の形によって異なるので、それぞれの状況を考えながら式をたてなければならない。
- 円環内の熱の不等速運動の方程式
円環(リング)の場合、熱伝導方程式はこのようになる。C は物体の比熱、D は物体の密度をあらわす。

- 固体球内の熱の不等速運動の方程式
中身の詰まった球の場合、熱伝導方程式はこのようになる。

- 固体円筒内の熱の不等速運動の方程式
無限に長く、中身の詰まった円筒形だとこのようになる。
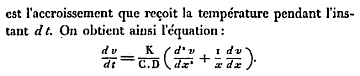
- 無限長の固体角柱内の熱の等速運動の方程式
無限に長く、中身の詰まった角柱だとこのようになる。

- 固体立方体内の熱の不等速運動の方程式
中身の詰まった立方体だとこのようになる。これが「フーリエの熱伝導方程式」と呼ばれているものだ。

このように2階の偏微分方程式であらわされる熱伝導方程式のほか、この章では物体の表面から散逸する熱についての方程式も紹介される。具体的にここでは示さないが、これは1階の偏微分方程式であらわされている。
第3章:無限長の長方形固体内の熱の伝播
第2章で求めた熱伝導方程式を第4章以降でそれぞれ解いていくのだが、第3章では手始めとして「2次元の板」という簡単な例で熱伝導方程式をたてて、解くことを試みている。この章で熱伝導方程式を解くための方法としてフーリエ級数が紹介される。
例題として持ち出した物体は上に向かって無限に伸びた長方形の板だ。その厚さは無視して2次元物体として取り扱う。板の底辺をY軸にとり底辺の長さをπとする。縦方向(上方向)をX軸にとる。板の上の任意の点は座標(x,y)であらわす。
板の底辺は温度「1」の熱浴に接し、底辺はいつでも温度が「1」の状態とする。
板の左右の辺は温度「0」の熱浴に接し、両辺の温度はいつでも「0」とする。
初期状態は底辺の温度だけ「1」で、板のその他の温度はすべて「0」である。
時間がたつにつれて底辺にある熱は上方向(Xのプラス方向)に伝わっていく。十分な時間がたつと熱平衡状態(定常熱伝導)に達し、板の上の温度はそれ以上変化しない状態になる。このときの板の上の熱(=温度に比例)の分布を座標(x, y)の関数として求めたい。
これが与えられた問題である。
熱伝導方程式と変数xに対する条件は次のようになる。板の両サイドの温度が「0」というのが境界条件に使われる。またここで温度 v は関数φ(x,y)であらわされる。板の両サイドの温度は常に0という境界条件は φ(x,±1/2*π)=0 として要請する。

変数yに対する条件も必要だ。板の底辺の温度は常に「1」なのでφ(0,y)=1 を要請する。

この方程式を解くためにフーリエ級数という方法が考察され、最終的に次の形で紹介される。これを導く過程で三角関数どうしの直交性が使われている。

方程式を解く過程はとても込み入っているので、ここで紹介することはできないが、最終的にフーリエは次の解にたどりつく。温度 v の分布を板上の座標 x と y であらわすとこのようになった。

そこでWolframAlphaという数式処理サービスを使って最終的な定常状態の温度の分布を見てみよう。
WolframAlpha
http://www.wolframalpha.com/
フーリエが得た解をあらわす式をvについて解いたものをWolframAlphaに入力すると板の温度分布のグラフが得られた。白っぽいところほど温度が高い。(WolframAlphaで確認したい方はここをクリック。)
WolframAlphaへは次のように入力する。
=2/pi*arctan(2cos(y)/(exp(x)-exp(-x))) x=0 to 5 y=-pi/2 to y=pi/2
結果はこのとおり。板の両サイドの温度が0に固定されているので、熱は中央に寄る形に分布する。また底辺から離れるに従って温度は低くなっている。


上の例は板の底辺の温度がすべて1の場合だが、フーリエはさらに板の底辺の温度分布が関数 f(y) であらわされるような一般的な場合についての解にも到達している。それは次のようなものだ。

第4章:円環内の熱の線形および不等速運動
第2章でたてたそれぞれの形の物体の熱伝導方程式に対して、第4章からその解を求めていく。これらはすべて時間変数 t を含む非定常解だ。それぞれ解いた結果を紹介するだけにしておこう。解はそれぞれ無限級数であらわされている。
円環(リング)の場合の解はこうなる。初期状態として与えた円環の温度分布が時間の経過とともに広がり、さらに円環は温度0の空気に接し円環から空気に熱が流れ出るような条件を設定して解を求めている。

第5章:固体球内の熱の伝播
初期状態で全体が均一な温度1の球を温度0の空気にさらすという条件で、球内部の温度分布がどのように変化するかという問題の解を求めている。

第6章:固体円筒内の熱の運動
円筒全体を一様な温度にした後、続いてそれを加熱し中心軸から同じ距離にあるすべての点が同じ温度になったとする。それをより冷たい空気の流れにさらす。ある与えられた時刻での異なった層(中心軸から等距離の面)の温度を決める問題である。解は次のようになる。
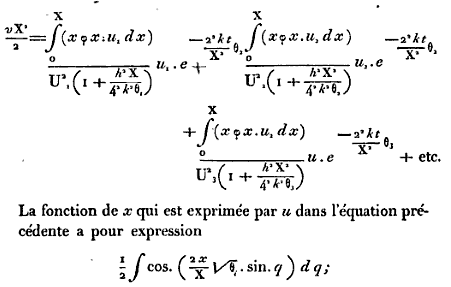
第7章:長方形角柱内の熱の伝播
初期状態として角柱の底面を温度Aに、他の部分を温度0の空気中にさらす。このとき角柱の与えられた点が取りうる最高温度を求める。解は次のようになる。(このケースでは解に時間変数 t は含まれない。)
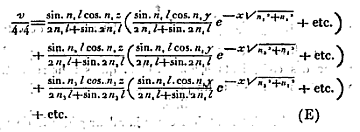
第8章:固体の立方体内の熱の運動
初期状態として全体を均一な温度にした立方体を、温度0の空気中にさらす。このとき立方体について、時間がt経過したときの温度分布を求める問題だ。解は次のようになる。

第9章:熱の拡散
「フーリエ変換」と「フーリエ逆変換」が紹介されているのがこの章だ。これを使って寸法が無限大の固体の中で熱が拡散していく様子を計算する。この章だけで100ページほどあり、計算過程はとても込み入っている。
まずフーリエ変換と逆変換が次のように導かれる。

- 無限長の一つの線内の熱の自由運動
1次元の熱伝導の問題だ。このような熱運動方程式になる。

この節ではさまざまなケースについて考察し、解を求めているので一概には解を紹介できないのだが、たとえばこのような解を求めている。

- 無限長固体内の熱の自由運動
3次元になると熱伝導方程式はこのようになる。

そしてその解のひとつの表現がこれだ。
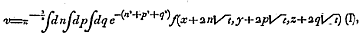
この章の残りの部分では、無限長固体内の最高温度を求める方法を紹介したり、微分方程式の解がさまざまな表現を取りうること、どのような表現を採用すべきかということについて解説を行っている。
訳者あとがき
竹下先生が本書の翻訳をすることになった経緯、翻訳の元となるフランス語版や英語版のテキストをどのように入手されたか、本書内の数学的な箇所について数学者に助言をいただいたことが書かれている。
本書を通じて理解できたその他のこと
- 熱伝導方程式の解の一意性について
フーリエ級数やフーリエ変換によって得られる熱伝導方程式の解となる関数が一意に収束することは、本書の中でフーリエも述べている。しかしそれは数学的には厳密なものではなく、解の一意性と収束性の証明は後の数学者たちに託されることになる。
- 熱伝導とフーリエ展開、フーリエ変換の関係について
フーリエは熱伝導方程式の解をフーリエ展開して表示したとき、無限級数に展開された各項がそれぞれ熱の物理的な現象と結びついていると考えていたことが本書の記述によってわかる。しかしそれは誤りで、フーリエ展開やフーリエ変換はあくまで熱伝導をあらわす偏微分方程式を解くための手段のひとつと考えるべきだということが理解できた。
- 偏微分方程式がフーリエ級数やフーリエ変換で解けることについて
偏微分方程式がフーリエ級数で解けるのは、展開された各項がすべてその偏微分方程式の特殊解となっているからである。それは熱伝導方程式の線形性による。最終解としての関数が偏微分方程式の一般解となるのはこの理由による。
- 物体の形の違いによって熱伝導の偏微分方程式の形が異なる理由の本質は、採用する直角座標、球座標、円柱座標など座標系の違いであることがわかった。
ネット上に公開されている文書について
なお、ネット上には次の文書があり、本書のエッセンスはこれら2つ文書に凝縮されている。購入を検討されている方は、前もって目を通しておくとよいだろう。
「熱の解析的理論」
熱方程式の導出に至る過程
(本書の第1章、第2章:フーリエの法則と熱伝導方程式の導出)
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1317-03.pdf
「熱の解析的理論」
Fourier 展開公式と Fourier 積分公式 その Fourier 自身による証明
(本書の第3章、第4章、第9章:フーリエ級数やフーリエ変換の導出)
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1257-8.pdf
ご覧になるとわかるが、フーリエ級数やフーリエ変換は三角関数を使った表示であり、よりエレガントなネイピア数 e の指数関数を使った表示(オイラーの公式を使った表示)にはなっていない。
今回はこのように方程式と解をピックアップして紹介しただけだが、本書の醍醐味はあらゆる解析学のテクニックを駆使してフーリエ級数やフーリエ変換、熱伝導方程式などを解き明かしていく過程にある。およそ200年前にフーリエが切り開いたこの道筋は知性と数理科学の開拓精神にあふれたものだった。
------------------------
2019年12月に追記:
今回の記事で紹介したのは大学教育出版の本だ。同じタイトルの本が朝倉書店から12月16日発売される。
「フーリエ 熱の解析的理論」(紹介記事)

この2冊の違いを朝倉書店に問い合わせたところ、次のような回答をいただいた。購入を予定されている方は、参考にしていただきたい。
大学教育出版様から出版されている『熱の解析的理論』はフーリエの死後G. ダルブーが編纂したエディションを底本にしており、今回弊社より刊行する翻訳書ではフーリエが出版した1822年版を中心に底本として参照しております。また監訳者・訳者による歴史的解説もぜひご注目いただければ幸いです。
------------------------
関連記事:
発売情報: フーリエ 熱の解析的理論(朝倉書店)
https://blog.goo.ne.jp/ktonegaw/e/5d9e583dd2ed1de0ed2b9e70325bbc04
高校数学でわかるフーリエ変換:竹内淳
https://blog.goo.ne.jp/ktonegaw/e/aa1e79d97684f88319d9d4e96e6a89a3
伝熱工学(東京大学機械工学):庄司正弘
https://blog.goo.ne.jp/ktonegaw/e/cdbbfe5c89a57b812d43448297966fcc
伝熱工学 (JSMEテキストシリーズ):日本機械学会
https://blog.goo.ne.jp/ktonegaw/e/bfd58adf704e39cb64ca95224c7262b5
なっとくする偏微分方程式:斎藤恭一
https://blog.goo.ne.jp/ktonegaw/e/16d054ebc14ad1c4336f2b9f997eb00c
図解 熱力学の学び方 (第2版):北山直方
https://blog.goo.ne.jp/ktonegaw/e/f48fd3b842e6330e42fe682dd680e315
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。





「熱の解析的理論:ジョゼフ・フーリエ著、ガストン・ダルブー編纂」(電子書籍)

編者まえがき
序論
第1章:総論
- 著書の目的
- 一般概念と予備定義
- 熱の授受の原理
- 熱の等速で、線形的な運動
- 薄い角柱内の恒久温度の法則
- 閉じられた空間の加熱
- 三次元内の熱の等速運動
- 固体の任意の点の熱の運動の測定
第2章:熱の運動方程式
- 円環内の熱の不等速運動の方程式
- 固体球内の熱の不等速運動の方程式
- 固体円筒内の熱の不等速運動の方程式
- 無限長の固体角柱内の熱の等速運動の方程式
- 固体立方体内の熱の不等速運動の方程式
- 固体内の熱の伝播に関する一般方程式
- 表面に関する一般方程式
- 一般方程式の応用
- 一般的考察
第3章:無限長の長方形固体内の熱の伝播
- 問題の概要
- 熱の理論に三角級数を用いた最初の例
- 級数に関する考察
- 一般解
- 解の結果からえられた最終式
- 三角級数による任意の関数の展開
- 実際の問題への応用
第4章:円環内の熱の線形および不等速運動
- 問題の一般解
- 離れた物体間の熱の伝達
第5章:固体球内の熱の伝播
- 一般解
- この解に関するいくつかの考察
第6章:固体円筒内の熱の運動
第7章:長方形角柱内の熱の伝播
第8章:固体の立方体内の熱の運動
第9章:熱の拡散
- 無限長の一つの線内の熱の自由運動
- 無限長固体内の熱の自由運動
- 無限長固体内の最高温度
- 微分方程式の解の比較
訳者あとがき
内容(「BOOK」データベースより)
本書は、ジョゼフ・フーリエ(1768-1830)の原書をおよそ70年後に数学者ガストン・ダルブー(1842-1917)が編纂したものを訳したものである。全文9章663頁からなる。熱伝導の方程式は第2章、フーリエ展開公式は第3章、方程式の解は第4-9章で紹介する。
翻訳者:竹下 貞雄 (たけした さだお)
1933年 福井市に生まれる。
1958年 京都大学卒業
1958年 日本国有鉄道入社
1964年 ベルギーのリェージュ大学留学(1年)
1983年 鉄道技術研究所,土質研究室長
1985年 工学博士(京都大学)
1986年 立命館大学理工学部教授
2009年 同上退職。
現在は翻訳業に従事している。
理数系書籍のレビュー記事は本書で211冊目。(直前の記事までに紹介した大村平先生の著書4冊は大学受験前に読んだ本なのでカウントには含めないことにした。)
今回は歴史的な名著を読んでみた。先月「高校数学でわかるフーリエ変換:竹内淳」を紹介したのは本書を念頭においてのことだったのである。
科学史上の名著のひとつ
フランスの数学者、物理学者のジョゼフ・フーリエ(1768-1830)が1822年に著した「Theorie analytique de la chaleur」という本の日本語訳だ。(正確に言えば数学者ガストン・ダルブー(1842-1917)が編纂した1890年刊行本の日本語訳である。)これは19世紀でもっとも重要な書物のひとつと言われている。
フーリエはこの中でフーリエ級数やフーリエ変換の方法をはじめて紹介し、これを使って固体の熱伝導現象を表す偏微分方程式を解析的に解いた。この本は数理科学、応用数学上きわめて重要な意味を持っている。


1822年の初版本は金沢工業大学ライブラリーセンターに所蔵されていて、次のページで説明を読むことができる。
ジャン・バティスト・ジョゼフ・フーリエ (1768-1839) 熱の解析的理論 パリ, 1822年初版
http://www.kanazawa-it.ac.jp/dawn/182201.html
フランス語版の著作権はとっくの昔に切れているので、ネット上では現在次の2つの版を読むことができる。(PDFファイルとしてダウンロードも可)
1822年刊行、フーリエ著のオリジナル(見てみる)
1883年刊行、フーリエ著、バロン版(見てみる)- バロン(baron)とは「男爵」の意味。
Archive.org: フランス語版を検索
理数系の外国語の文章は文学のように難解ではないので、フランス語の原典は仏検2級レベルの読解力と理数系大学1、2年レベルの数学力があればなんとか読めると思う。
フランス語版や英語版の書籍はそれぞれの国のアマゾンから購入できる。いろいろな版がでているのでお求めになるときは注意したほうがよい。ダルブー編纂の本は偏微分方程式に現代と同じ「∂」記号が使われているが、フーリエ(オリジナル)やバロンの本は「∂」のかわりに「d」が使われているからだ。(今回紹介した日本語版はダルブー編纂の翻訳なので「∂」を使っている。)
フランス語版:Theorie Analytique De La Chaleur:Amazon.co.jpで検索
英語版:The Analytical Theory Of Heat:Amazon.comで検索、Amazon.co.jpで検索
竹下先生が翻訳を始めた2004年頃はフランス語版、英語版共に入手が極めて困難だったことが「訳者あとがき」に書かれているが、幸い両言語共に近年になって発売されたことになる。
日本語版について
日本語版「熱の解析的理論:ジョゼフ・フーリエ著、ガストン・ダルブー編纂」を翻訳されたのは竹内貞雄先生。現在「ラプラスの天体力学論 全5巻」を翻訳されている。
「熱の解析的理論」が日本語版として刊行されたのは2005年のことである。「訳者あとがき」によると翻訳はフーリエの原書(1822)を用いたが、説明文の中に数式が入っていることが多く、現在のテキストとは違和感があるので途中からダルブー編纂(1890)のものを使ったそうだ。本は科学雑誌Newtonと同じ大判のB5サイズで、340ページ。読み応えは十分ある。数学的な記述レベルは理数系大学1、2年で足りるが、読み通すのにはかなりの忍耐が要求される。
「熱の解析的理論」はその後、紙の本は絶版になり電子書籍が発売された。またフランス語原典に関しては、以下の種類のものが無料で公開されている。
1. 大学教育出版(電子書籍):開く
2. 1822原著:開く
3. Darboux編・Fourier全集t.1:開く
4. (参考)Fourier全集t.2(完):開く
5. reprint (Gabay):開く
本書を読んだ理由
このタイミングで僕がこの本を読んだのには、次のような理由が重なっていたからだ。
- 今年に入ってから物理学科で学ぶ熱力学の本を集中的に読んでいる。もっと遡れば「ファインマン計算機科学」を読んで情報エントロピーと熱力学エントロピーの関連性を知ったことに端を発している。熱力学のメインは第1、第2、第3法則だ。けれどもこの中には時間変数 t があらわれない。時間変数 t を使う熱の理論というのは熱伝導や伝熱学のことだ。これらについても学びたいと思ったから。
- 本書を翻訳された竹内貞雄先生による「ラプラスの天体力学論」の第5巻が今月末に発売され、全5巻が揃う予定。先生の著作(翻訳)を紹介するにはよいタイミングであること。そして、この記事が竹内先生のお目にとまるかどうかはわからないが、翻訳された本を真面目に読んだ人がここに一人いることを示しておきたいという気持ちもある。
- フーリエの人生はおよそ200年前のフランス革命やナポレオンの時代と重なっている。当時の解析学のレベルを実感してみたいと思ったこと。
- フーリエ級数やフーリエ変換と熱伝導の関係をしっかり理解したいと思ったこと。これは現代の教科書でもよいわけだが、発想や思考過程を追うためにはやはり最初に理論を開拓したご本人の著作を読むのがいちばんだと思ったから。
- コンピュータによる数値計算を使わない解析的手法(数式だけの計算)で、熱伝導をどこまで記述でき、解を得られるかということに関心があったから。
- 基礎となる原理は「フーリエの法則」というごくシンプルなものだが、熱伝導の対象となる物の形が違うと、偏微分方程式で表される熱の運動方程式やその解き方がどれくらい違ってくるのかということに関心があったため。
フーリエの法則:物体を通過する伝熱速度は、熱の流れに垂直な断面積(伝熱面積)に比例し、流れの方向に沿った温度勾配の符号を変えたものに比例する。単位伝熱面積当たりにすると 熱流束密度 J=-λ(dT/dx)と書ける。
これだけの理由があったから僕はどうしてもこの本が読みたかった。日本語版の新品本は売切れていたので値段の高い中古本しか手に入らない。アマゾンの画面をにらみながら「うーむ、どうしよう。。。」と悩む間もなく購入ボタンをクリックしたのだった。
フーリエにとって「熱」とは?
フーリエがこの本を出したのは1822年。「熱学思想の史的展開:山本義隆」の第3巻に書いたように熱がエネルギーのひとつの形態であることがわかったのは1850年以降のことだ。フーリエの時代は同書でいえば第2巻の前半、ラヴォアジエの「熱素説」やラプラスの「熱量学」が受け入れられていた時代で、フーリエの考えもこれに近かった。そして当時は絶対温度の概念も生まれていなかった。水の凝固点と沸点を基準にその間を等分する目盛を温度計に採用していたから測定値は不正確だったわけだ。
彼が物質としての熱素を信じていたかどうかは本書には書かれていないが、熱は物体の中を移動し、その総量は変わらないから「熱流体」のように取り扱うことができるということは述べられていた。50年後に熱力学第一法則が導かれ、熱は仕事に転換できるエネルギーの一種であることがわかるので、「熱流体」や「熱流束」として計算しても結果が正しいことは後に確認されることになる。
本書がメインテーマとする「熱伝導」とは、固体の中や表面を熱が移動することであり、ざっくばらんな言い方をすれば物体の中を「熱がジワジワと伝わる現象」のことだ。対流や放射など熱伝導以外の方法で熱が伝わることを認識していたことをフーリエは本書で述べている。
フーリエは物質を構成する「分子」についても言及し、その中を熱が伝わると説明している。ただし彼の言うところの分子とはニュートン力学の流れをくむラプラス流、純粋に力学的なもので、物質を構成する粒子として遠距離では万有引力の法則に従い、それらが接するほど近距離では斥力を及ぼし合うという説だった。その数理的なメカニズムは確立されていない。熱流体はそのような分子の中を透過的にすり抜けて伝わっていくと考えたのだ。
物体の比熱や物体の中の熱伝導率、表面から外に出るときの熱伝導率については、物質それぞれについて測定値としてすでに得られていて、フーリエはその結果を熱伝導方程式に取り入れている。
現代における熱伝導の解釈
原子や分子の構造や力学が詳しく解明された現代において熱伝導は原子の「格子振動の伝達と伝導電子の移動」として理解されている。ウィキペディアの「熱伝導の項」では次のように説明されている。
熱伝導:物質の移動を伴わずに高温側から低温側へ熱が伝わる移動現象のひとつである。熱伝導は、フォノン及び伝導電子が担う。特に、金属においては、伝導電子が熱伝導の主要な担い手である。通常の物質では伝導電子による寄与の方が大きいので、金属は半導体や絶縁体(フォノンが主要な熱伝導の担い手)よりも熱伝導性が良い。しかし、非常に硬いダイヤモンドではフォノン(格子振動)を介した熱伝導性の寄与の方が非常に大きくなる。
イメージとしてはこのようなもの。左が伝導電子の移動、右が格子振動だ。

格子振動を量子化したものが「フォノン(音響子)」と呼ばれる準粒子で、音響フォノンと光子フォノンの2種類がある。このうち音響フォノンが熱伝導にたずさわっている。(ウィキペディアの「フォノンの項」を参照)
詳しく知りたい方は、次のようなページをお読みになるとよい。
熱が伝わるとは?
http://okwave.jp/qa/q384684.html
音響フォノンは熱を運んで光学フォノンが熱を運ばない理由
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1395015953
カーボンナノチューブの熱伝導シミュレーション(PDF)
http://www.jim.or.jp/journal/j/pdf3/73/08/583.pdf
伝熱学で使われる用語の説明
現代では熱伝導は伝熱学、伝熱工学の中の一分野として分類されている。伝熱工学は熱の輸送方法の違いによって大まかに次の内容から構成されている。
1)熱伝導(Heat Conduction) =伝導伝熱(Conductive Heat Transfer)
2)対流熱伝達(Convective Heat Transfer)
3)輻射伝熱(Radiative Heat Transfer)、 熱輻射=熱放射(Thermal Radiation)
4)相変化を伴う伝熱(Heat Transfer with Phase Change)
5)熱拡散(Heat Diffsion):固体の場合、物質の拡散に伴う場合
日本語について言えば「伝熱」はいちばん大きなくくりで、固体のときは「伝導」や「伝播」、液体や気体の対流の場合は「伝達」のように使い分けられている。
本書の第8章までは「熱伝導」を取り扱い総和記号Σを使ったフーリエ級数を使う理論、第9章は「熱拡散」を取り扱い積分記号∫を使ったフーリエ変換の理論である。
本書の内容詳細
前置きが長くなったが、章立てに沿って本書の内容を紹介しよう。目次の詳細はこの記事のいちばん下を参照していただきたい。
編者まえがき
編者ダルブーによってフーリエの業績が紹介される。フランスの数学者ダルブーが生まれたのはフーリエの死後12年経った1842年のことである。「まえがき」の中でダルブーはフーリエの熱の理論の研究が1807年の論文要約および1811年の論文が元になっていることや、1822年に「熱の解析的理論」が本として出版されるまでの経緯を説明している。
序論
フーリエ自身による解説はここからはじまる。序論では次のことが述べられている。
- 熱の研究はきわめて大切だが、まだ解明されていない。
- 熱の研究、科学の歴史はアルキメデス以前まで遡ることができる。
- ニュートン力学の普遍性、適用範囲がきわめて広いこと。
- ニュートン力学では熱の挙動を説明できないこと。
- 熱の挙動は少数の事実で説明できること。
- 熱の影響は地球や太陽、大陸や海、気象全般におよび、その研究は物理学や経済に多大な利益をもたらすこと。
- 熱伝導は微分方程式によって解析的に解けること。本書がそれを解説するものであること。
- それまでにフーリエがフランスの科学アカデミーに提出した論文やその評価について。
- 熱の測定結果は数学に結び付けられ進歩していくものであること。
第1章:総論
経験的事実を論理的に積み重ねる形で、「フーリエの法則」が成り立つことを導いている。そのかなめとなるのは物質内の「熱の移動」という現象が温度の高い場所から低い場所に向かう方向で発生し、「重ね合わせ」ができるという事実にある。(線形性が成り立つ。)
この記事ではジョゼフ・フーリエに敬意を払い、フランス語の原書から該当箇所を切り出す形で紹介しよう。
フーリエの法則は、次のように表記されている。本書では全体を通じて温度に対して v や w という変数が使われている。

また、この章では熱の運動には時々刻々変化する「非定常熱伝導」と時間が経過して熱平衡状態に達している「定常熱伝導」があることが解説されている。
そしてこの章では測定値として求められる外的伝導率 H や内的伝導率 K が導入される。外的伝導率は物体の表面から内部に流れ出す熱の伝導率で、内的伝導率は物体の内部で移動する熱の伝導率のことだ。(注意:伝熱学では外的伝導率のことは「熱伝達率」という用語が使われている。)
第2章:熱の運動方程式
前章の結果を利用しながら、この章では熱伝導が行われる物体で成り立っている熱の運動方程式が偏微分方程式の形で紹介される。式は物体の形によって異なるので、それぞれの状況を考えながら式をたてなければならない。
- 円環内の熱の不等速運動の方程式
円環(リング)の場合、熱伝導方程式はこのようになる。C は物体の比熱、D は物体の密度をあらわす。

- 固体球内の熱の不等速運動の方程式
中身の詰まった球の場合、熱伝導方程式はこのようになる。

- 固体円筒内の熱の不等速運動の方程式
無限に長く、中身の詰まった円筒形だとこのようになる。
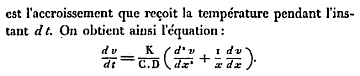
- 無限長の固体角柱内の熱の等速運動の方程式
無限に長く、中身の詰まった角柱だとこのようになる。

- 固体立方体内の熱の不等速運動の方程式
中身の詰まった立方体だとこのようになる。これが「フーリエの熱伝導方程式」と呼ばれているものだ。

このように2階の偏微分方程式であらわされる熱伝導方程式のほか、この章では物体の表面から散逸する熱についての方程式も紹介される。具体的にここでは示さないが、これは1階の偏微分方程式であらわされている。
第3章:無限長の長方形固体内の熱の伝播
第2章で求めた熱伝導方程式を第4章以降でそれぞれ解いていくのだが、第3章では手始めとして「2次元の板」という簡単な例で熱伝導方程式をたてて、解くことを試みている。この章で熱伝導方程式を解くための方法としてフーリエ級数が紹介される。
例題として持ち出した物体は上に向かって無限に伸びた長方形の板だ。その厚さは無視して2次元物体として取り扱う。板の底辺をY軸にとり底辺の長さをπとする。縦方向(上方向)をX軸にとる。板の上の任意の点は座標(x,y)であらわす。
板の底辺は温度「1」の熱浴に接し、底辺はいつでも温度が「1」の状態とする。
板の左右の辺は温度「0」の熱浴に接し、両辺の温度はいつでも「0」とする。
初期状態は底辺の温度だけ「1」で、板のその他の温度はすべて「0」である。
時間がたつにつれて底辺にある熱は上方向(Xのプラス方向)に伝わっていく。十分な時間がたつと熱平衡状態(定常熱伝導)に達し、板の上の温度はそれ以上変化しない状態になる。このときの板の上の熱(=温度に比例)の分布を座標(x, y)の関数として求めたい。
これが与えられた問題である。
熱伝導方程式と変数xに対する条件は次のようになる。板の両サイドの温度が「0」というのが境界条件に使われる。またここで温度 v は関数φ(x,y)であらわされる。板の両サイドの温度は常に0という境界条件は φ(x,±1/2*π)=0 として要請する。

変数yに対する条件も必要だ。板の底辺の温度は常に「1」なのでφ(0,y)=1 を要請する。

この方程式を解くためにフーリエ級数という方法が考察され、最終的に次の形で紹介される。これを導く過程で三角関数どうしの直交性が使われている。

方程式を解く過程はとても込み入っているので、ここで紹介することはできないが、最終的にフーリエは次の解にたどりつく。温度 v の分布を板上の座標 x と y であらわすとこのようになった。

そこでWolframAlphaという数式処理サービスを使って最終的な定常状態の温度の分布を見てみよう。
WolframAlpha
http://www.wolframalpha.com/
フーリエが得た解をあらわす式をvについて解いたものをWolframAlphaに入力すると板の温度分布のグラフが得られた。白っぽいところほど温度が高い。(WolframAlphaで確認したい方はここをクリック。)
WolframAlphaへは次のように入力する。
=2/pi*arctan(2cos(y)/(exp(x)-exp(-x))) x=0 to 5 y=-pi/2 to y=pi/2
結果はこのとおり。板の両サイドの温度が0に固定されているので、熱は中央に寄る形に分布する。また底辺から離れるに従って温度は低くなっている。


上の例は板の底辺の温度がすべて1の場合だが、フーリエはさらに板の底辺の温度分布が関数 f(y) であらわされるような一般的な場合についての解にも到達している。それは次のようなものだ。

第4章:円環内の熱の線形および不等速運動
第2章でたてたそれぞれの形の物体の熱伝導方程式に対して、第4章からその解を求めていく。これらはすべて時間変数 t を含む非定常解だ。それぞれ解いた結果を紹介するだけにしておこう。解はそれぞれ無限級数であらわされている。
円環(リング)の場合の解はこうなる。初期状態として与えた円環の温度分布が時間の経過とともに広がり、さらに円環は温度0の空気に接し円環から空気に熱が流れ出るような条件を設定して解を求めている。

第5章:固体球内の熱の伝播
初期状態で全体が均一な温度1の球を温度0の空気にさらすという条件で、球内部の温度分布がどのように変化するかという問題の解を求めている。

第6章:固体円筒内の熱の運動
円筒全体を一様な温度にした後、続いてそれを加熱し中心軸から同じ距離にあるすべての点が同じ温度になったとする。それをより冷たい空気の流れにさらす。ある与えられた時刻での異なった層(中心軸から等距離の面)の温度を決める問題である。解は次のようになる。
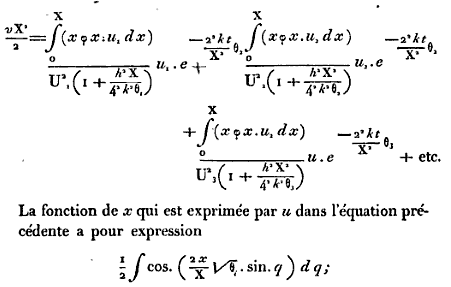
第7章:長方形角柱内の熱の伝播
初期状態として角柱の底面を温度Aに、他の部分を温度0の空気中にさらす。このとき角柱の与えられた点が取りうる最高温度を求める。解は次のようになる。(このケースでは解に時間変数 t は含まれない。)
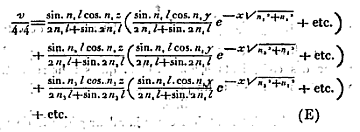
第8章:固体の立方体内の熱の運動
初期状態として全体を均一な温度にした立方体を、温度0の空気中にさらす。このとき立方体について、時間がt経過したときの温度分布を求める問題だ。解は次のようになる。

第9章:熱の拡散
「フーリエ変換」と「フーリエ逆変換」が紹介されているのがこの章だ。これを使って寸法が無限大の固体の中で熱が拡散していく様子を計算する。この章だけで100ページほどあり、計算過程はとても込み入っている。
まずフーリエ変換と逆変換が次のように導かれる。

- 無限長の一つの線内の熱の自由運動
1次元の熱伝導の問題だ。このような熱運動方程式になる。

この節ではさまざまなケースについて考察し、解を求めているので一概には解を紹介できないのだが、たとえばこのような解を求めている。

- 無限長固体内の熱の自由運動
3次元になると熱伝導方程式はこのようになる。

そしてその解のひとつの表現がこれだ。
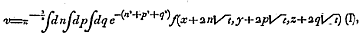
この章の残りの部分では、無限長固体内の最高温度を求める方法を紹介したり、微分方程式の解がさまざまな表現を取りうること、どのような表現を採用すべきかということについて解説を行っている。
訳者あとがき
竹下先生が本書の翻訳をすることになった経緯、翻訳の元となるフランス語版や英語版のテキストをどのように入手されたか、本書内の数学的な箇所について数学者に助言をいただいたことが書かれている。
本書を通じて理解できたその他のこと
- 熱伝導方程式の解の一意性について
フーリエ級数やフーリエ変換によって得られる熱伝導方程式の解となる関数が一意に収束することは、本書の中でフーリエも述べている。しかしそれは数学的には厳密なものではなく、解の一意性と収束性の証明は後の数学者たちに託されることになる。
- 熱伝導とフーリエ展開、フーリエ変換の関係について
フーリエは熱伝導方程式の解をフーリエ展開して表示したとき、無限級数に展開された各項がそれぞれ熱の物理的な現象と結びついていると考えていたことが本書の記述によってわかる。しかしそれは誤りで、フーリエ展開やフーリエ変換はあくまで熱伝導をあらわす偏微分方程式を解くための手段のひとつと考えるべきだということが理解できた。
- 偏微分方程式がフーリエ級数やフーリエ変換で解けることについて
偏微分方程式がフーリエ級数で解けるのは、展開された各項がすべてその偏微分方程式の特殊解となっているからである。それは熱伝導方程式の線形性による。最終解としての関数が偏微分方程式の一般解となるのはこの理由による。
- 物体の形の違いによって熱伝導の偏微分方程式の形が異なる理由の本質は、採用する直角座標、球座標、円柱座標など座標系の違いであることがわかった。
ネット上に公開されている文書について
なお、ネット上には次の文書があり、本書のエッセンスはこれら2つ文書に凝縮されている。購入を検討されている方は、前もって目を通しておくとよいだろう。
「熱の解析的理論」
熱方程式の導出に至る過程
(本書の第1章、第2章:フーリエの法則と熱伝導方程式の導出)
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1317-03.pdf
「熱の解析的理論」
Fourier 展開公式と Fourier 積分公式 その Fourier 自身による証明
(本書の第3章、第4章、第9章:フーリエ級数やフーリエ変換の導出)
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1257-8.pdf
ご覧になるとわかるが、フーリエ級数やフーリエ変換は三角関数を使った表示であり、よりエレガントなネイピア数 e の指数関数を使った表示(オイラーの公式を使った表示)にはなっていない。
今回はこのように方程式と解をピックアップして紹介しただけだが、本書の醍醐味はあらゆる解析学のテクニックを駆使してフーリエ級数やフーリエ変換、熱伝導方程式などを解き明かしていく過程にある。およそ200年前にフーリエが切り開いたこの道筋は知性と数理科学の開拓精神にあふれたものだった。
------------------------
2019年12月に追記:
今回の記事で紹介したのは大学教育出版の本だ。同じタイトルの本が朝倉書店から12月16日発売される。
「フーリエ 熱の解析的理論」(紹介記事)

この2冊の違いを朝倉書店に問い合わせたところ、次のような回答をいただいた。購入を予定されている方は、参考にしていただきたい。
大学教育出版様から出版されている『熱の解析的理論』はフーリエの死後G. ダルブーが編纂したエディションを底本にしており、今回弊社より刊行する翻訳書ではフーリエが出版した1822年版を中心に底本として参照しております。また監訳者・訳者による歴史的解説もぜひご注目いただければ幸いです。
------------------------
関連記事:
発売情報: フーリエ 熱の解析的理論(朝倉書店)
https://blog.goo.ne.jp/ktonegaw/e/5d9e583dd2ed1de0ed2b9e70325bbc04
高校数学でわかるフーリエ変換:竹内淳
https://blog.goo.ne.jp/ktonegaw/e/aa1e79d97684f88319d9d4e96e6a89a3
伝熱工学(東京大学機械工学):庄司正弘
https://blog.goo.ne.jp/ktonegaw/e/cdbbfe5c89a57b812d43448297966fcc
伝熱工学 (JSMEテキストシリーズ):日本機械学会
https://blog.goo.ne.jp/ktonegaw/e/bfd58adf704e39cb64ca95224c7262b5
なっとくする偏微分方程式:斎藤恭一
https://blog.goo.ne.jp/ktonegaw/e/16d054ebc14ad1c4336f2b9f997eb00c
図解 熱力学の学び方 (第2版):北山直方
https://blog.goo.ne.jp/ktonegaw/e/f48fd3b842e6330e42fe682dd680e315
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。

「熱の解析的理論:ジョゼフ・フーリエ著、ガストン・ダルブー編纂」(電子書籍)

編者まえがき
序論
第1章:総論
- 著書の目的
- 一般概念と予備定義
- 熱の授受の原理
- 熱の等速で、線形的な運動
- 薄い角柱内の恒久温度の法則
- 閉じられた空間の加熱
- 三次元内の熱の等速運動
- 固体の任意の点の熱の運動の測定
第2章:熱の運動方程式
- 円環内の熱の不等速運動の方程式
- 固体球内の熱の不等速運動の方程式
- 固体円筒内の熱の不等速運動の方程式
- 無限長の固体角柱内の熱の等速運動の方程式
- 固体立方体内の熱の不等速運動の方程式
- 固体内の熱の伝播に関する一般方程式
- 表面に関する一般方程式
- 一般方程式の応用
- 一般的考察
第3章:無限長の長方形固体内の熱の伝播
- 問題の概要
- 熱の理論に三角級数を用いた最初の例
- 級数に関する考察
- 一般解
- 解の結果からえられた最終式
- 三角級数による任意の関数の展開
- 実際の問題への応用
第4章:円環内の熱の線形および不等速運動
- 問題の一般解
- 離れた物体間の熱の伝達
第5章:固体球内の熱の伝播
- 一般解
- この解に関するいくつかの考察
第6章:固体円筒内の熱の運動
第7章:長方形角柱内の熱の伝播
第8章:固体の立方体内の熱の運動
第9章:熱の拡散
- 無限長の一つの線内の熱の自由運動
- 無限長固体内の熱の自由運動
- 無限長固体内の最高温度
- 微分方程式の解の比較
訳者あとがき























