
掲載画像:複素平面(ガウス平面)に描かれたマンデルブロート集合の図形
今月号の「ニュートン」で虚数についての特集記事が掲載されていることを紹介したので、この記事では虚数や複素数の世界が実世界とつながっていることについて書こうと思う。それはもちろん複素数を図示するための「複素平面(ガウス平面)」が実数の数直線を含んでいるからということではない。
この記事に掲載している数学の公式は中学と高校で学習するもので、式に含まれる変数や係数は実数を前提にしている。そして2次方程式では解が複素数になるものがあることを学び、数が実数から虚数や複素数に拡張されることが紹介される。
これらの公式は実をいうと複素数の変数や係数でも成り立っているのだ。実世界の公式(=法則)と同じものが複素世界でも成り立っているのは、不思議であり当たり前のようでもある。例えてみると宇宙に行ってみたらそこでも日本国憲法に従って宇宙人が生活していたというような話なのだから。
目に見える実世界の法則が目に見えない複素世界まで延びているのだ。そしてそれを成り立たせる「理由」がどこかにあるはずだ。不思議かどうかはともかくとして、少なくともそれは実世界と複素世界の間に境界線は存在しないのだということを強く感じさせてくれる。
簡単な例からはじめよう。学校で習う2次方程式は係数 a, b, c が実数で、かつ a≠0 の場合だ。

この x についての方程式の解は次のような式であることを覚えているだろうか?

ここでもし係数の a, b, c が複素数だとしたら、2次方程式に対して x の解はこの公式のままでよいのだろうか?答えはYesなのだ。そして一般に x の解は複素数になる。(実数になる場合もある。)
係数 a, b, c が複素数のときでも同じ公式が成り立つわけを説明しよう。2次方程式の解の公式を導く方法を思い出してほしい。忘れてしまった方はこのページをご覧になるとよい。
この一連の計算手順の中で使われているのは加減乗除(+-×÷)と指数法則など実数で使われる演算規則だけである。複素数の演算規則は実数のときと全く同じだから、a, b, cが実数の場合と同じ手順で式変形したとしても、実数のときの計算手順は複素数の場合でもそのまま当てはまる。
つまり2次方程式の解の公式は係数 a, b, c が複素数の場合も成り立つことが理解できた。
三角関数についてはどうだろうか?角度を x とすれば高校で習う三角関数は次の3つだ。

意外に思うかもしれないが x が複素数でも三角関数は定義できるのだ。複素数の世界の三角関数では x はもはや「角度」という意味がなくなってしまっている。角度であるべき変数が複素数だというのは幾何的にイメージできないが、それはどのような世界だろう?
虚数を紹介するときに出てきたオイラーの公式から複素数の三角関数の公式を導くことができる。

オイラーの公式に対してその共役形を求める。共役形とはこの図の式ようなものだ。(この図では変数を x でなく θ としているが、x と読み替えて理解してほしい。)
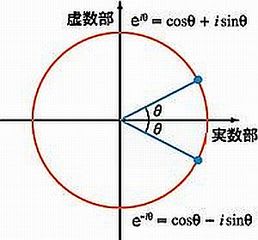
オイラーの公式とその共役形を連立させ、辺々足し算したり引き算したりすると次の2つの式が得られる。

この2つの式で x は実数なのだが、実はこの x に複素数を代入してもそのまま成り立っているのだ。つまり左辺は複素数の三角関数になるから、複素数についても三角関数が e の指数関数として定義できるわけである。つまりこうなる。

三角関数は変数が実数でも複素数でも定義できるのだ。(tan xについては tan x = sin x / cos x で定義できる。)
さらに三角関数の加法定理はどうだろうか?次の一連の公式の角度αとβは実数だけでなく、複素数であっても成り立っているのだ。証明は面倒だが挑戦してみてほしい。

双曲線関数の加法定理についても実数と複素数で同じ公式が成り立っている。
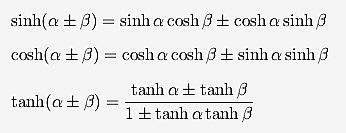
対数関数については注意が必要だ。

は x や y が実数でも複素数でも成り立つのだが

は x が実数では成り立つものの複素数では成り立たない。これは複素対数関数が多価関数であることによる。
微積分についてはどうだろうか?実数関数についての以下の微分の公式は複素数変数の場合でもすべて成り立っている。

複素数を変数とする関数の値は複素数だから、複素関数というものも考えることができる。そしてそれらの微分について、実数関数で成り立つ以下の公式もそのまま成り立つ。

積分(不定積分)は微分の逆演算だから、複素数の場合もそのまま成り立つことは言うまでもないだろう。
このように実数世界の公式は複素数世界でも成り立っているのだ。もちろんすべて成り立つというわけではない。
たとえば「三角形の内角の和は180度である。」や「ピタゴラスの定理」などの公式は複素数世界で三角形という図形を定義できないのだから、そもそも成り立つはずがない。
学校で新しい公式(=法則)を習うとき、それが複素数の世界でも成り立っているか、それとも別の形で拡張されるのかを考えながら先生の話を聞くと、いつもの授業もまた別のものに思えてくるだろう。
ところで複素数の世界で成り立つ法則(=公式)がすべて実数世界で成り立つわけではない。複素数の世界には複素数独特のとても美しく、不思議な法則(=公式)がたくさんあるのだ。複素変数 z = x + yi (x, yは実数)に対して関数 f(z) は一般に複素数になり、これを複素関数と呼んでいる。
複素関数は大学の数学の「複素関数論」や「複素解析」という授業で学ぶことができるので、興味のある方はその道に進まれるとよいだろう。
ネットでこの世界を知りたい方のために、お勧めサイトを2つ紹介しておこう。
複素関数論入門(ときわ台学)
http://www.f-denshi.com/000TokiwaJPN/12cmplx/000cmplx.html
複素関数論入門
http://next1.msi.sk.shibaura-it.ac.jp/MULTIMEDIA/complex/complex.html
次の記事につづく。
応援クリックをお願いします!

関連記事:
虚数は私たちの世界観を変えてしまった。
https://blog.goo.ne.jp/ktonegaw/e/ed35400df27a2bc7e597531c08d99869
虚数や複素数に大小がないのはなぜ?
https://blog.goo.ne.jp/ktonegaw/e/398b0d7e84eb491dea9c38a15e994256
複素数 a+bi のプラス記号は「足す」という意味?
https://blog.goo.ne.jp/ktonegaw/e/e29c7f0e787464693ff26ab287b34ddd
博士の愛した数式とGoogleの電卓機能
https://blog.goo.ne.jp/ktonegaw/e/0d7855769ea29ddd42d0ddad25f13046
虚数の情緒
https://blog.goo.ne.jp/ktonegaw/e/27155c8d7b5242d7e69e00335411acc1
ヴィジュアル複素解析
https://blog.goo.ne.jp/ktonegaw/e/2f47e7b748d4ca7022dc53305388a00b
因数分解って何の役に立つの?
https://blog.goo.ne.jp/ktonegaw/e/e54dfcd47b72ae247a22206c05bfaa8e
























今月号の虚数の記事は、面白いですね。
僕も月刊のほうのNewtonは滅多に買いません。
> 今月号の虚数の記事は、面白いですね。
さすがNewtonという感じでビジュアルに虚数を紹介していますね。
数学的な内容はもちろん知っていますが、家庭教師とかで教えるときにいい教材になるなと思い、僕も1冊買いました。
そのうち「別冊ニュートン」のほうで「虚数」をテーマにしたのが出版されるかもしれませんね。でもこのテーマでまるまる1冊にするには少々ネタ不足かも??