そもそもどうして入射角と反射角は等しいのだろうか?
ファインマン物理学の第2巻の冒頭。光学の理論にはいるところでふと考えてしまった。高校物理どころか小学校の理科でも教わる「常識」であるはずなのに、自分はその理由を答えられないことに気がついたのだ。このままでは気になって眠れない。深夜にもかかわらずこのような記事を書いているのはそんなわけである。
光線の場合には入射角と反射角が等しいことは感覚的に納得しやすい。
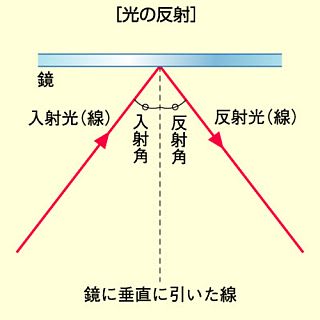
光が粒子であろうと波であろうと、このことは正しいように思える。
ビリヤード球が斜めから壁にぶつかるときだって同じ理屈が成り立つのだと授業では習うし、試験のときもこの法則を「無条件に」使う。
けれどもビリヤード球は大きさのある剛体だから回転についての慣性モーメント(回転のしにくさをあらわす量)があるはずで、それを考えに入れてもこのことは成り立っているのだろうか?これがそもそもの疑問の発端である。もしかしたらビリヤード球のときは入射角と反射角は等しくないのでは?と思ったのだ。
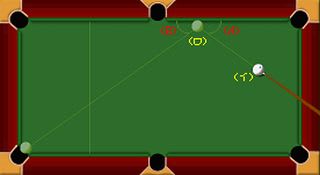
強く突くと球は回転せずにビリヤード台の上をすべり、このような感じで壁に反射する。このときは回転についての慣性モーメントを考えなくてもよいので入射角と反射角は等しく思える。図では球は手前から壁にぶつかり右方向にはじき返されることをあらわしている。
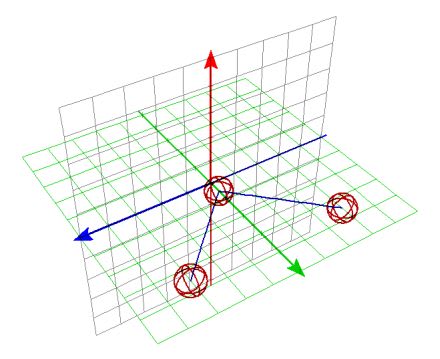
しかし、無重力空間に浮かんだ壁面にビリヤード球を回転させずに衝突させた場合を考えてみる。ビリヤード台はないものとしよう。慣性の法則により直進していく球は衝突後には上から見て左回りに回転するはずなので、そのトルク(力)を受けたために反射角は本来の進行方向よりも手前になると想像できる。
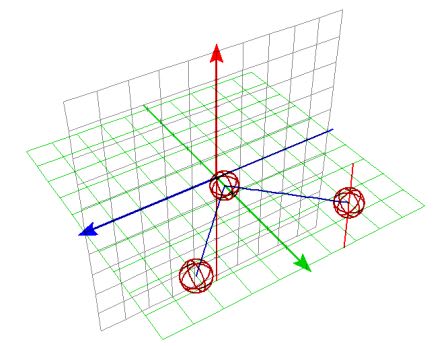
さらに次の場合はどうだろう。ビリヤード台の上で球をゆっくり突いたらどうなるだろうか?すべらずに転がりながら壁にぶつかるはずであり、反射後も転がっていくはずだ。図では球の回転軸を赤い直線で示している。
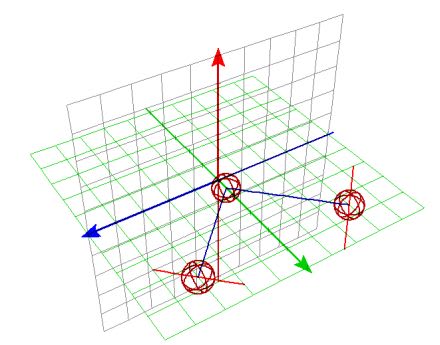
壁に衝突した瞬間、球には壁の摩擦力によって図の青軸方向のトルク(力)が働くはずである。その結果、球は上から見て左回転するはずだ。そして衝突の前後では球のころがりの回転軸も瞬間的に変化する。詳しい力学はともかく球の角運動量が変化することは確かだ。この場合どう考えても入射角と反射角が同じになるとは思えないのだ。
さらに球を突く強さを「中間的」にし、衝突の前では回転はなく衝突後にころがる場合だって考えられる。ころがり摩擦や壁面での衝撃吸収によって衝突の前後で減速するようなケース。このときに考えられる回転の力学も上のものと違ってくるだろう。それをあらわしたのがこの図だ。
計算で証明できていないので説得力には乏しいのだが、学校で習う「入射角と反射角は等しい。」はどうも疑わしいのである。
入射角と反射角を等しくさせない理由は回転についての慣性モーメントのほかに、壁の材質による理由もありそうだ。
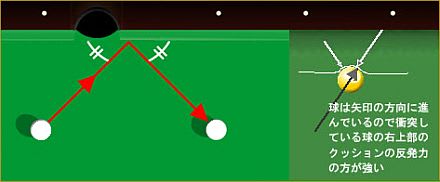
ビリヤードの場合、壁の材質もやわらかいので球が衝突する瞬間、上の図のように球の進入方向と反射方向に違う大きさの反作用の力が働く。明らかに進入方向に働く反作用の力のほうが大きいのだ。
このため反射した球は入射角と同じ角度の反射方向と想定される直線よりも手前にはじき飛ばされることになる。これが入射角と反射角を等しくさせない2つ目の理由だ。
ビリヤードの上級者ならば入射角と反射角が等しくないことは常識なのかもしれない。それにもかかわらず僕は学校で習ってきたとおりのことに全く疑問を感じず、そのまま信じ込んでいたのだ。浅はかなことだ。
ビリヤード球の入射角と反射角が等しくないことを上手に説明しているページを見つけたので紹介しておこう。なるほどと納得するはずだ。
ビリヤード基礎知識(バンク反射)
http://www.paostyle.tv/billiard/contents/kiso_bank_hansya.html
そもそもビリヤードは球のどの部分を突くかによってさまざまな「変化球」が生まれるものだ。曲線を描いて転がすことだってできる。どのような回転の状態で壁に衝突するかによっても反射角は変化してしまう。ビリヤードの変化球については次のページをご覧になるとよい。なかなか複雑なものである。
ビリヤードの変化球について説明しているページ
http://www.sbygd.net/tcat3.html
こう考えると学校で教わる「入射角と反射角は等しい。」は理想的条件で成り立つことがおぼろげにわかる。しかし現実のビリヤード球のように大きさのある剛体のときは本質的に間違っているのではないか。理想的条件にできるのはせいぜい壁の固さだけで、回転についての慣性モーメントの影響は依然として残ってしまう。
------------------
翌朝に追記:
眠れずに考えていたところ、学校で教わる「入射角と反射角は等しい。」は理想的条件で成り立っているのだということが詳しくわかってきた。ビリヤード球と壁の接触時間が無限小でかつ完全弾性衝突をする場合、壁が球を押す力は垂直成分しかないからビリヤード球の速度の壁に平行な成分には影響を与えない。だから「入射角と反射角は等しい。」ことが成り立つわけだ。
しかし、現実にはこの接触時間は無限小ではないのと完全弾性衝突でないため、接触時における球の回転の具合によって異なる力が壁と平行な方向に働く。そのために「入射角と反射角は等しくない。」ということがおきる。接触時間には壁と球の材質の他に球の速度と質量も関係してくるだろう。また壁に垂直な方向の反発係数(はねかえり係数)も衝突後の球の速度の壁に垂直な成分に影響を与えるはずだ。
つまり入射角と反射角が等しくなくなる要因は
1)接触時間の長さ
2)反発係数(はねかえり係数)
3)摩擦係数(ころがり摩擦係数とすべり摩擦係数のどちらなのか?)
4)接触点で球が壁から受ける反発力の大きさと方向。これは接触時の球の回転方向とその「角速度x球の慣性モーメント」、3)の摩擦係数によって変わる。
の4つであるのだと思える。そしてこれら4つは独立ではなさそうだ。しかし僕にはまだそれらの関係がよくわかっていない。3)は4)を得るために必要だし、4)と1)も衝突後の球の速度に影響を与えそうである。
「完全弾性衝突」を仮定することで、これら4つの要因は無視できるようになる。学校で習う物理学は全く都合のよいものだ。
更に考察を深めると、このあたりの「跳ね返り」のからくりは壁面と球を構成する原子配列の格子モデルや応力テンソルのモデルで解明されるのかもしれない。それとも電子のクーロン力による反発力のモデルまで考えるべきなのだろうか。いずれにしても物性物理学の範疇であるにはちがいない。摩擦係数や反発係数という実験値がこれらのモデルから導けるのかどうかは興味深い問題だ。
よく考えてみれば、靴底と地面は完全弾性衝突していず摩擦力が働いているから僕らは前に走れるのであり、車は前進することができるわけだ。もし完全弾性衝突していればつるつるすべって前に進めるはずがない。だから現実世界の球の衝突現象では入射角は反射角に等しくないことがはるかにもっともらしいと思えるのだ。
------------------
今日の説明は定性的なものに終始したが、いつかこれを数式計算で証明してみたいものだ。これだから力学はあなどれない。学校で習うことを鵜呑みにしてはいけないのだ。
というわけで、一応は納得したので今夜は安心して眠れそうだが、いや待てよ。光のときはどうして入射角と反射角が同じになるのだろう?
光を粒子と考えればビリヤード球のようになるのではないか?波動と考えると壁の表面ではどんな現象がおきているのだろう?そのことから説明がつくのだろうか?
やはり「ファインマン物理学 第2巻:光、熱、波動」を読んでみるしかあるまい。
応援クリックをお願いします!このブログのランキングもこれらのサイトで確認できます。


関連記事:
入射角と反射角は等しいのだが...(光学)
https://blog.goo.ne.jp/ktonegaw/e/3de82981c21df98ddb1521c1da452227
「ファインマン物理学」のレビューを参照したい方、購入したい方はそれぞれ画像をクリックしてください。





























よってビリヤード球は壁とぶつかった場合、壁に垂直な方向にしか力を受けないんではないしょうか。 つまりF=F⊥+F// とした場合F//=0。 よって衝突の際に平行な方向への運動量は保存すると思われます。 ∴ p//=一定。
また垂直な方向へは弾性衝突の条件から、エネルギーが保存、よって運動量の大きさも保存。 ∴p'⊥=-p⊥ 。よって衝突の際、反射角は等しくなる。
と、いっても、ビリヤードの球に回転をかけると壁との衝突の際F//が生じるので、反射角は等しくならないと思います。学生時代球に急激なスピンをかけつつも、球をゆっくりとすすませると、壁に垂直に当たっても壁にそってすすませることができました。波の場合は、ホイヘンスの原理をつかって干渉で説明がつくんだったんだと思います。
壁も球も完全に「つるつる」だったら入射角と反射角は等しくなりますね。単原子からできている気体の分子が壁に衝突するときなんかはそうなるのではとも思いましたが、そのような場合は壁面もミクロの視点に立てば「でこぼこ」ですしね。
摩擦力の本質が難しいように衝突の瞬間に働いている力学って一筋縄ではいかないのかもしれません。もう少し考えてみることにします。また眠れなくなりそうです。(笑)
話の次元は違うのですが、球が転がりながら衝突する前後で回転軸が一瞬のうちに変化する現象は電子のスピンが量子力学的に離散的に変化する様子に似ていて面白いですね。もちろん球の場合は古典力学的な現象なわけですけれども。
剛体とは少し違う話なのですが、私には
「なぜ光が反射するとき、入射角と反射角が等しくなるか?」
という疑問があって、はっきりと説明できないでいます。
光子が鏡面の原子にぶつかって、たぶん鏡面の原子が励起して、
再度光子が投げ出されるのだとしたら、360度全方向に放り出されてもよさそうに思うのです。
実はブログねたにしようと思って考えたのだけれど、これぞといった説明に思い至りませんでした。
その後、アトムさんのアドバイスや僕自身が見落としていたことも見つかり、もう少し詳しくわかってきました。そのことは本文中の「翌朝に追記」というところに書いておきましたのでお読みください。
波動としての光についての原理はファインマン物理学の第2巻で説明していると思います。光子とみなす場合の説明は僕も見たことがありません。rikunoraさんがおっしゃるように360度全方向に散乱してしまいそうですよね。よく考えてみると光子の運動方向は不確定性原理によって定まりませんから、光線の進行方向と一致するはずもありません。
今回のネタは面白そうなので、もう少し追求してみようと思います。
最近は「ご冗談でしょう、ファインマンさん」系の本にはまってしまい、なかなかブログ更新できません。(笑)これらの本については近いうちに記事にする予定です。
興味ありますね。
光が原子一個にぶつかる場合ですら難しそう。光が電子一個にぶつかる場合はコンプトン散乱と呼ばれているんでしたっけ。その場合は360度万遍無く散乱されるんだったのかな・・・・。なんか角度依存性があった気がするけどエネルギーにも依ってるのかな。
とそんなところから考え直している今日この頃です。
光の場合について、その後考えつづけていますが、ファインマンの径路積分あたりを紹介しつつ、光線が最短時間になるようなルートを進み、入射角と反射角の問題を解説する記事を書く予定です。かなり興味深い記事になりそうです。元ネタは「虚数の情緒」という本の中にあるので、僕のオリジナルネタではないですが。。。
鏡の面でどのような反射のからくりがあるのかについては、まだまだ調査中です。コンプトン散乱あたりもじっくり研究してみます。
のぶゆきさんがおっしゃるように、気体の分子運動論でも同じことが言えます。特に2原子分子、3原子分子などでは複雑なことになるでしょう。それにそのサイズだと不確定性原理による反射角の乱れもでてきますし。
分子運動論で入射角や反射角が取り上げられることが少ないのは、角度が違っていても私たちが感覚的に違いを感じるような物理現象がないからなのでしょう。熱力学や統計力学は無限の数の分子の全体としての効果を研究する学問ですし。
入射角と反射角については「光学」の場合についても近々記事に書きますので楽しみにしていてください。
少しお役に立てるかも知れないのでレスさせて頂きます。
-----
ビリヤードの世界ではずっと昔から、入射角と反射角を等しくさせない主要な理由は「クッションの変形」と言われてきましたが、ショックなことに10年ほど前にほぼ否定されてしまいました。
そもそもこの「クッションの変形」という発想は、ビリヤード上級者なら誰でも知っている「ハードショットすればするほど反射角が立ってくる(反射角が小さくなる)」「ソフトショットなら反射角は寝る」という経験則を良く説明していて、上級者なら誰もが思い至るごく自然な発想だったと思います。
30年以上前に執筆された世界的なビリヤードのバイブルである、「ビリヤード・スタンダードブック」(ロバート・バーン著)でもその理論が書いてあり、それ以前にまして長く「常識」とさえ考えられてきました。
しかしあろうことかその後、上記ロバートバーン氏自らが「ビリヤード・コンプリートブック」の中でこの考えを否定します。スタンダードブックから20年以上経ってのことです。
氏はクッションについて丸々1章を割き、相当な強打でなければ「手球が無回転でクッションに入った場合、速度の違いは反射角に殆ど影響を与えない」ことを表す実験を多数掲載しています。実際のショットでは、軌道を変えるほどクッションを凹ませるハードショットは少ないということです。
因みにその実験は同時に、「ショットの強弱で反射角が変わるのは、ハードショットのときのボールは概ね無回転、ソフトになればなるほどラシャとの摩擦でボールが前回転していることが多いから」ということを示唆したものでした。(後述C)
長くなるので一旦切ります。
-----
・反射角を減少させるパラメータ
A)クッションからの貰い捻り (とね様の3番目の図)
捻り(=左右の回転)を持たないボールでも、反射後は貰い捻りを得る。
動く歩道に垂直落下したボールと同様、回転しながら本来より斜めに跳ねる。
(実践的には最初から順捻りを掛けてこの影響を抑えることも多い)
例:充分な摩擦があり、射出時の回転がクッションに対して滑らずに転がっていたと想定した場合、例えば45度反射で本来(1、1)に進むべきベクトルが(0.6、1.0)に変化する。その日の湿度などにもよるが充分な摩擦が得られないこともある。
-----
・反射角を増大させるパラメータ
B)クッションの反発係数 (非弾性衝突)
クッションの平行成分をxとしてxを保存しながらy成分だけ減少させる。
例:反発係数0.75なら理論上(1、1)が(1、0.75)に変化する。
厳密に言うと、y成分だけでなくx成分も減少する。これはクッションの高さが
ボールの半径より高く、ボールがクッションの下にもぐりこむためである。その日の
湿度などで変わるが例えば(0.9、0.75)のような数値になる。
ここまでがAとBがボール無回転の場合です。以降は回転が加わります。
C)ボールの縦回転 (とね様の4番目の図)
ショット突入時のボールが縦回転している場合、反射後にまるで慣性的な力が働いたかのように変化する。
物理的にはボールは無回転が基本であるが、実践的には(横回転と違って)縦回転は有るのが基本である。AやBと違って上記の通りショットの強弱で大きく変動するCはバンクショットやワンクッションにおける最大パラメータでさえある。
例:ボールが転がり回転(回転モーメント2/5)であれば例えば45度(1、1)が理論値で(1.4、0.6)に変化する。ただし実際には縦回転の大部分(その日の湿度等にもよるが例えば50%とすると)はクッションとの摩擦で喰われるので例えば(1.2、0.8)のような数値になる。