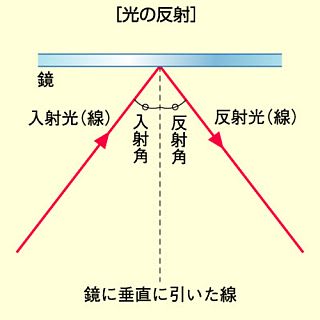
光が真っ直ぐに進むことや反射や屈折をしたときの光の経路は「フェルマーの原理(最小時間の原理)」で説明される。つまり鏡に反射する光線の入射角と反射角が等しくなるのは所要時間を最小にする、つまり最短経路を光が進むからだということになるわけだ。
小中学校ではこのように「入射角と反射角は等しい。」ことだけを教わり、高校や大学では「それは所要時間を最小にするためだ。」と教わるのだったと思う。
けれども、何かおかしいと思わなかっただろうか?
所要時間や経路の長さを最小にするためにはあらかじめゴール地点を知っていなければならない。光は出発した時点で目的地を知っていたのだろうか?目的地を知った上でまっしぐらにそこに向かって突き進んでいったのだろうか?。まさかそんなはずはあるまい。
つまりどうして「最小時間の原理」が成り立つのだろうか?
ということである。
これについていろいろ調べたところ、驚くべき事実がわかったので今日この記事で紹介することにした。
それは「光は最短経路だけでなく、可能なあらゆる経路を進んでいる。」というものだ。そんな馬鹿な!と思われるかもしれない。光の道筋は1本だけに見えるのだから。
こんな奇妙なことを言い出したのは頻繁に僕が引用しているファインマンであり、それは彼が30歳のときに発表した「経路積分」と呼ばれているものである。この「経路積分」は量子電磁力学(QED)や素粒子物理学の世界では世界中の物理学者に受け入れられ、当たり前な考え方として毎日のように使われているのだ。
量子力学によれば微小な粒子はすべて「シュレディンガーの波動方程式」を解いて得られる波動関数
 という複素関数であらわされる状態で存在している。
という複素関数であらわされる状態で存在している。
条件によって波動関数は時間 t や位置 x の関数になるので
 や
や  、
、  のように書かれたりする。実際に方程式を解いてみると、もっともシンプルな解は次のように書きあらわせる。(シュレディンガーの波動方程式についてはこの記事をお読みいただくとイメージがつかみやすいと思う。)
のように書かれたりする。実際に方程式を解いてみると、もっともシンプルな解は次のように書きあらわせる。(シュレディンガーの波動方程式についてはこの記事をお読みいただくとイメージがつかみやすいと思う。)
光を量子力学的にあらわすと、それは光子としてくるくる回る複素ベクトルによってあらわされる状態で空間を光速度 c で突き進むこの図のようなイメージになる。
図1:光が空間を進むイメージ
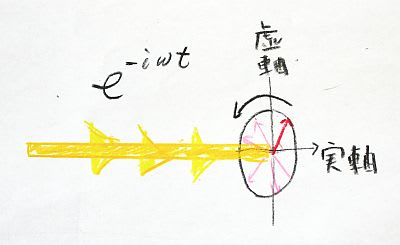
ωは角振動数で光が数センチ進む間に何万回ものすさまじい勢いで回転する。光の波長が短くなるほど、つまり赤い光より紫や紫外線のほうがωの値は大きくなる。
このような光を考え、光源Sと観測点Gと鏡を次の図のように置く。赤い経路は入射角と反射角が等しくなる経路、それ以外は「光源Sを出発して鏡に反射してから観測点Gに到達する。」という条件を満たすすべての経路である。(経路は無数にあるので途中を間引いているが。)鏡面上のF以外で反射する経路は入射角と反射角が一致していないことに注意してほしい。
図2:反射するすべての光の経路
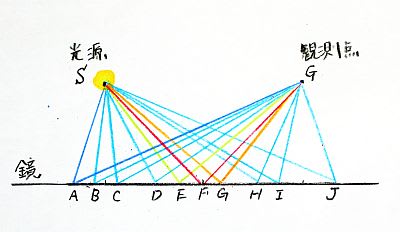
光子は光源Sを一斉に出発し、複素ベクトルを回転させながら突き進む。それぞれの光子が観測点に到達するまでの距離を縦軸にとるとそれは所要時間に比例するので、縦軸は所要時間とみなすこともできる。横軸はそれぞれの経路をあらわしている。それぞれの光子は観測点Gに到達した瞬間にそのベクトルの向きを観測することにしよう。その瞬間のベクトルの向きを表したのが横軸の下に描いた丸の中の矢印である。
図3:それぞれの経路の長さと観測点での微小ベクトル

量子力学では波動関数 ψ は複素数値でこれを「確率振幅」と呼んでいる。この確率振幅の絶対値(長さ)の2乗がその粒子の「存在確率」そのものになるのである。つまり上の小さなベクトルのそれぞれの長さは同じなので、それぞれの経路を通る光子の量はすべて等しいというわけである。
観測点Gに到達する光子全体の量はすべての経路を通って到達した微小ベクトルを合計すればよい。そしてその絶対値(長さ)の2乗を計算すればよいわけだ。正確に計算するためには「可能な経路すべてについて微小ベクトルを積分する」のだが、今回の説明は近似的なものなのでベクトルの矢印を合計してみよう。ベクトルの和は矢印をつなぎ合わせるだけなので簡単だ。
図4:微小ベクトルの合計
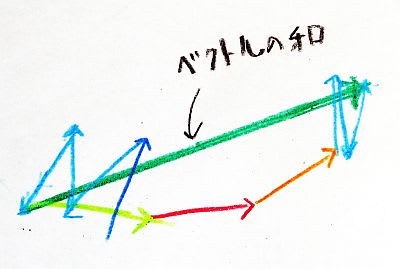
この緑のベクトルがすべての微小ベクトルを合計したものであり、緑ベクトルの絶対値の2乗が観測点Gに到達するすべての光子の量である。緑ベクトルは微小ベクトルにくらべてはるかに長いので、これは全光量が観測できるために十分なほど大きな量になっていることを示している。
ところでこの図をよく見ると、黄緑色と赤と橙色の3つの微小ベクトルの向きが揃っているため、緑ベクトルに長さを与えるために大きな役割を果たしていることがわかるだろう。これらは鏡面上ではE, F, Gで反射した光子たちである。また鏡面上で A~D、H~J など鏡の中央以外で反射している光子の微小ベクトルは向きが揃っていないため緑ベクトルの長さにはほとんど役立っていない。
それではどうしてE, F, Gで反射した光子たちの微小ベクトルの向きが揃うのだろうか?
図3で F は所要時間が最小になる点である。所要時間をあらわす曲線で値が最小になる点の接線は水平になる。つまり最小点での近くでは所要時間も似たりよったりになるため微小ベクトルの向きは同じ方向に揃い、観測点Gでの合計ベクトル(緑ベクトル)の長さに大きな影響を与える。
これが「最小時間の原理」が成り立っているからくりなのだ。最小時間の原理から「最短経路」が導かれ、そこから幾何学的な結論として入射角と反射角が等しくなるという観測結果が得られるわけである。
それ以外の反射点からの光子も観測点にちゃんと届いていることは不思議に思われるかもしれないが、これは事実である。反射点 F からの微小ベクトルだけでは緑色の合計ベクトルの長さを十分に得られないということから F 以外の場所からの反射も必要なことが容易にわかるだろう。
鏡の端のあたり、つまり反射点 A~D などからも光子が反射して観測点に届いていることは「虚数の情緒」という本でわかりやすく説明されている。実をいうと今回の記事の元ネタはこの本なのだ。この本では微小な複素ベクトルを使った方法で最小時間の原理の他、光の直進性、レンズのしくみ、回折格子のしくみ、波長の短い青い光は散乱されやすいために空は青く見えることなどをとても詳細に解説しているのでぜひお読みいただきたい。
「可能なすべての経路」は直線とは限らない。光子はこの図のように曲線に沿って進んでも構わない。
図5:可能なすべての経路

光子は目的地を知っているどころかこのように「幾何学も反射点も、入射角も反射角も、何も知らない」のである。(そのほうが理にかなっている。)ただ最小時間になる経路を進む光子だけが十分強い量となって観測されるだけなのだ。それは光が所要時間の似た経路が密集している場所に高い確率で存在するからだ。
ところで光子のように小さい粒子にとっては、鏡のようにつるつるな表面でさえ凹凸の激しいものになっているだろう。何せ光子は原子よりもはるかに小さいのだから。ハイゼンベルクの不確定性原理により、光子の反射方向はまったく不規則なものになるはずだ。そんな状況でもなお、光線はきっちり正確に光線として反射されるように見えているのである。
つまり、それは不規則に反射されているたくさんの光子のうち、狭い領域に集中している所要時間の似た光子だけが「光線」として観測されているだけにすぎないのだ。だから鏡面で光子はどのような角度で反射、散乱されていても最小時間の原理には全く影響を与えないことがわかる。
ところで「可能なすべての経路」とはどこまで考えればよいのだろうか?図2のA点より左にも反射点はあるだろうし、J点の右にも反射点はあるはずだ。厳密に経路積分を考えるとき、これは「どの範囲で積分するか」ということになる。
ファインマンによると積分範囲は「時間と空間についてマイナス無限大からプラス無限大」なのである。「えっ!そんな馬鹿な。。。」図で示すと可能な経路はこのようになる。空間の3次元はまとめて横軸にとった。ここで赤い線で示したのが最小時間の原理を満たす光の経路である。
図6:時空を横断する光子の経路
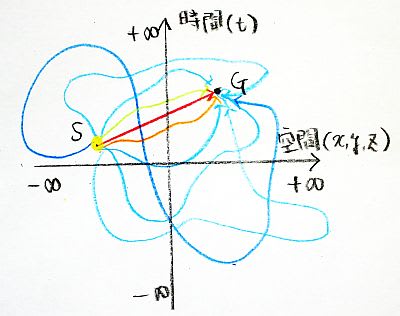
3億年前に存在していたパンゲア大陸に生息する恐竜の頭の上から現在の観測点Gに到着している光子もあり、今から5000年後の未来の大マゼラン星雲から時間を遡って現在の観測点Gに到着しているものもあるわけなのだ。うーむ、そんなことがあってよいものか。。。。
ところが素粒子物理学で扱う世界では、このようなことが当然のように起こっているのだ。ファインマンは経路積分の理論を発展させ次の図のような「ファインマン・ダイアグラム」というものを考案した。
図7:ファインマン・ダイアグラム
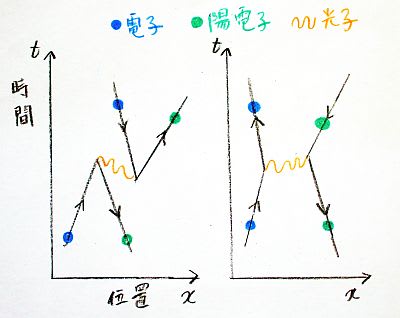
素粒子どうしの衝突により素粒子がどのように生成、消滅するかをあらわすための図だ。この図で大切なのは幾何学的なつながり方が同じであれば、線の傾きがどうであってもそれは同じ物理現象をあらわしていることだ。
つまりこの図のように時間をさかのぼる粒子は当然のように扱われている。また、線と線の交点で素粒子が衝突し生成、消滅するわけなのだが、それが起こる確率は交点ごとに計算し、可能なすべての組み合わせのファインマン・ダイアグラムを求め、それらの合計を求めるのである。これは経路積分の手法を使っているわけだ。
光子のように小さい粒子であればそれが何の粒子であれ、それは量子力学の法則に従って運動し、ファインマン・ダイアグラムを使ってそれがもたらす現象を解析することができる。光子や電子はまったく自由に未来と過去の間を行き来し、宇宙の果てからもう一方の果てまでやすやすと旅をしている。
「光の入射角と反射角は等しい。」や「光は最小時間の原理を満たす経路を進む。」のからくりの背後には驚くべき深い自然の摂理があったのである。
さらに言わせていただければ、量子力学の法則に従うと、可能なあらゆる経路を進む光子は「たった1つ」であっても構わないのだ。1つの光子が同時にあらゆる経路を進んでいる姿は僕にはうまくイメージできないのだが、直観的に理解できないということが量子力学の特色のひとつなのである。
-----------------------
今回紹介した光の進路の背景にある自然の摂理についての説明であるが、こういう切り口で科学番組を作ればよいと僕は思った。CGを使えば魅力的な映像ができるに違いない。光や電子の理論は最先端の素粒子物理学よりもはるかに身近でわかりやすい。相対性理論や量子力学は不思議で理解しにくいものだが、そういうものに人は惹かれるのだと思う。
学生時代の勉強の出来具合にかかわらず視聴率を稼げると僕は思う。1年半前にNHK BSで放送された「数学者はキノコ狩りの夢を見る ~ポアンカレ予想・100年の格闘~」(根上生也先生監修)はその成功例のひとつだ。番組ネタは山ほどあるのでテレビ番組関係者の方はぜひ検討していただきたい。将来のノーベル物理学賞受賞者の数は、どれだけこの手の番組の視聴率を稼げるかということに比例している。社会を変えるのはメディアの力である。
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。

関連記事:
入射角と反射角は等しくない。(力学)
http://blog.goo.ne.jp/ktonegaw/e/4006e853566b0d053227078f30cbdda1
























光子にシュレディンガー方程式を適用するところで、思考停止してしまうのです。光=電磁波は波動ですが、マクスウェル方程式の解なので、電子の波動関数のように複素数であることはなく、実関数だと思うのです。量子論的に考えれば、電場・磁場は物理量なので演算子に対応しますが、状態ベクトルには対応しないと思います。ここが分からないところです。
いただいたご質問は「光の光子としてのあり方を認めた上で、光子に量子力学を適用できるか。」ということと「光子としての光のあり方から電磁波としての光のあり方」を導くことができるかということに翻訳できますね。
光=電磁波(電場・磁場)つまり実数波であると考えてもこの記事の説明のように「位相のずれ」により最小時間の原理や屈折、回折などの現象は説明できますが、解析的(数式的)に経路積分をすることは困難になりますし、ファインマン・ダイアグラムに発展させることも困難になります。ですので今回の記事は光=光子という図式であることが前提になります。すると光子も電子と同じように波動関数は複素数(状態ベクトル)になると思うのです。このことについて僕は一般的な量子力学の教科書に書かれていることを鵜呑みにしているだけで満足してしまっているわけです。
光=電磁波 or 光子についてですが、電磁波と考えたときの角振動数(ω)と光子と考えたときの、つまりこの記事でのωは等しくなります。光子としての図式から電場と磁場がどのように生じているのかというからくりは僕にはまだ理解できていません。光子が電子どうしによって交換されるという「量子電磁力学」や「素粒子物理学」をまだ学んでいないからなのか、あるいはもっと別のからくりで理解しなければいけないのか、今後も勉強を続けていきたいとおもいます。
T_NAKAさんが期待されている回答になっているか、あまり自信がないのですが、今のところ僕がお答えできるのはこの程度のことです。
今後もT_NAKAさんのブログを参考にさせていただきたいと思います。
量子力学の教科書での光子の扱いは黒体輻射・光量子仮説・コンプトン効果などに出てくるだけで、真正面から光子の挙動を書いてないような気がします。
(これらの教科書は、多粒子系である場の量子論に踏み込む手前なので、光子というのは概念だけの説明をしているんじゃないかと考えています。)
「電磁場の量子化」というと、次にあるように、「マクスウェル方程式が光子に対する《シュレーディンガー方程式》の役割を果たしている」と解するのが一般的かと。
http://www1.cnc.jp/r_b_kyoutei/soutairyousitopic.htm
すいません。別に絡んでいる訳ではなく、私は量子力学を最初に学んだときの「光子」に対する違和感が強いのです。「光子にシュレディンガー方程式を適用する」とサラっと書かれていると気になって仕方がなく、コメントを書きました。つまり私の独白のようなものなので、お手数をお掛けして申し訳ありませんでした。
ご指摘を受けて「なるほど」と思いました。確かに量子力学の教科書には光子に対してシュレディンガーの波動方程式を適用する例は見かけたことはありませんね。たいてい電子に適用しているようです。
二重スリットの実験で光子と電子の場合の量子性を解説している例はありますので、光子の場合も電子と同様な「量子力学的存在」=「複素数の確率振幅を持つ」=「シュレディンガー方程式の解」なのだと僕は理解しておりました。ご指摘をうけてハッとしました。ありがとうございます。
今は出先(出社中)ですので教科書や書籍を調べることができないですし、ネット上の情報を鵜呑みにするのも好ましくないとは思いますが、この点について調べてみました。
ひとつだけ気が付いたのは岡部先生の量子力学のページで、光子も確率振幅を持つ(つまり複素数の波動性を持つ)ことが述べられているようです。
http://www.moge.org/okabe/temp/quantum/node5.html
光子に複素的な波動性があるのかどうかはもう少し調べてみます。(もしないのだとするとファインマンの径路積分はどうなってしまうのかなぁ、という気がしていますので。)特に電磁場の量子化によって浮かび上がる光子について調べてみます。
> すいません。別に絡んでいる訳ではなく
承知しております。むしろコメントやご返事いただいてうれしく思っています。私自身の理解も深まりますし、この記事をお読みになる方のより深い理解や議論のきっかけになるかとも思いますので。
私自身は大学では物理学を専攻していませんでしたので、専門に勉強をされた方のコメントやアドバイスは大歓迎です。
光子とシュレディンガー方程式との結びつきは両者を直接関連させて説明している箇所はありませんでしたが、光子がexp(-iωt)型の複素数の関数によってあらわされることが確認できました。
1)量子力学 II 第2版(朝永振一郎著)、285ページの最後の段落。(第9章「量子力学的状態」)
2)ファインマン物理学V、62ページの上あたり。式(4.24)の上あたりの記述。
3)古典場から量子場への道(増補第2版)、143ページからの説明。(電磁場の量子化についての節です。)
1)と2)は出版年が古いので、最近の学説とは異なっているのかもしれません。
「量子力学で分からないこと、、場の量子論をちょっと 」
http://teenaka.at.webry.info/200610/article_25.html
「場の量子論について(5)」
http://teenaka.at.webry.info/200901/article_19.html
さて、ご指摘の教科書で所有しているのはファインマン物理学Ⅴだけなので、それを確認しましたが、これは光子そのものの状態関数ではなく、[
光子がn個存在している]というような状態を示すものではないかと思えました(個人的感想なので勘違いがあるかも知れませんが)。
残念ながら僕は場の量子論をほとんどと言っていいほど勉強していませんから、ご紹介いただいた2つの記事とコメントを読んでみたのですが、むずかしくて内容についていけませんでした。もう少し勉強してから再度読ませていただきます。
ファインマン物理学Vの該当箇所についてですが、この章(第4章)の最初から10ページほどを読むと、僕にはどうしても光子は複素数であらわされる状態であると読めてしまうのです。大まかな流れで僕が読み取った内容を要約すると次のようなものです。
1)光子はボース粒子である。
2)56ページの「2個のボース粒子の状態」というセクションでボーズ量子の状態をディラックのブラ・ベクトルやケット・ベクトルで表示している。
3)ブラ・ベクトルやケット・ベクトルは複素数ベクトルである。
4)この部分で説明している内容はボーズ粒子の存在確率で、その計算の元にしているのはブラ・ベクトルやケット・ベクトルであるので、これらのベクトルは確率振幅(複素数)をあらわしている。
自分がどう理解しているとかいうレベルではなく、そう書いてあるのが読み取れるというレベルなものですから、少し恐縮ですが。
ところで、このブログの右欄に「お勧めリンク集」という枠を追加し、T_NAKAさんのブログも推薦させていただきました。これからもよろしくお願いいたします。
これからもお付き合い願います。
さて、以下は私の考えで、これが正しい認識であるとか、言い張る積もりは有りません。
ただ、「状態ベクトルが複素数=振動解」にはならないのではないか?という疑問です。
電場・磁場というのは直接計測できる物理量ですが、状態ベクトル(関数)というのは計測できるものじゃないですね(間接的に分かるものだと思います)。標準的な量子力学では、「物理量に対応するオペレータ・状態ベクトル=固有値・状態ベクトル」 ということで、固有値=測定値 というふうに理解しております。電磁波は電場・磁場の波動なので、物理量そのものがすでに振動していることになります。つまりオペレータや固有値(の集合)が振動していると捉えており、光子における波動関数とは、状態ベクトルではなくて、オペレータになると思います。
そうすると、状態ベクトル(複素数であるとしても)波動関数である必要はないと思うのです。
状態ベクトルの在り様についてのご説明ありがとうございます。電場・磁場という実数の物理量がどのように量子力学や素粒子物理学から生じるのか、僕も今後学んでいきたいと思います。見えない世界のことなので想像力や類推力は重要ですね。
先ほど書店で「日経サイエンス」を(少しだけ)立ち読みしてきました。その中に「特集:量子力学の実像に迫る
存在確率マイナス1 天才アハラノフの予言」というのが特集されていました。こうなると僕には全く想像がつきません。不思議な世界ですよね。
こちらのリンクで少しだけご覧いただけます。
http://www.nikkei-science.com/page/magazine/0910/200910_022.html
"Direct observation of Hardy's paradox by joint weak measurement with an entangled photon pair"
http://www.iop.org/EJ/article/1367-2630/11/3/033011/njp9_3_033011.html
式(4)で確率が -1 になると書いてありますね。
どうも「日経サイエンス」は素人を驚かすような記事ばかりで、感心しないのですが。。