◎【ミニ講座】(5) 相対速度
「相対速度」という言葉を聞いたことがありますか。
高校の物理でやることになると思いますが、そんなに難しくありません。
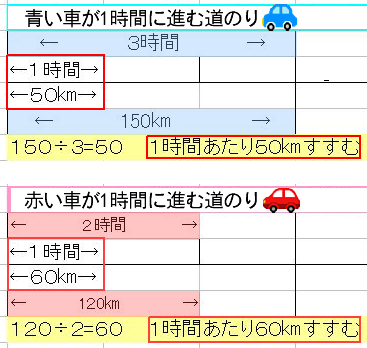
電車が時速80kmで走っていて、その脇を自動車が時速100kmで走っているとすると、電車の中から自動車を観察すると時速20kmで走っているように見える、というやつです。
簡単に言うと、観測する場所の速さを引いてあげるということですね。
これは進行方向が同じ場合です。進行方向が逆の場合は足すことになります。
上の例ならば、自動車が反対方向に進むならば時速180kmで遠ざかるように見えるということです。
この「相対速度」の使い所ですが、動くものが二つ以上ならば、使うことを検討すべきだと思います。
「旅人算」も「時計算」も「流水算」も「相対速度」を使って解くことが可能です。
普通の問題はわざわざ「相対速度」の考え方を使うまでもなく解けてしまうことが多いのですが、複雑な問題では「相対速度」の威力が発揮されることが多いです。
例えば、「流水算」で有名な問題に、次のようなものがあります。
<問題>
船Aは静水時の速さが一定です。
船Aが川を上流に向かってのぼっている最中に川を流れる浮き輪とすれ違いました。
その後、上流のP地点で折り返し、川を下る途中で先ほどの浮き輪に追いつきました。
船Aが最初に浮き輪とすれ違ってからP地点に着くまで10分かかったとすると、P地点から浮き輪に追いつくまで何分かかりましたか。
(答)10分
相対速度の考え方を使えば簡単なのですが、数字に頼る解法しか身に着けていない場合は解答不能かもしれません。
考え方のポイントは観察する場所を浮き輪にすることです。
浮き輪から見れば船Aは静水時の速さで遠ざかっていき(上り)、静水時の速さで近づいてきます(下り)。
浮き輪からP地点までの距離は同じですから、かかる時間も同じという結論になります。
実際にこの問題を解く時は、「時間が同じだから10分」で良いのですが、考え方を知っておくことも非常に大切です。
そのほか「相対速度」を使いたいのは、動くものが3つ以上の時です。
「周回運動」や「図形上の点の移動」の問題でよくあらわれます。
3点のどれか1つを止めてあげる(その点を観察点とする)ことによってかなり単純化することができると思います。
この考え方を使えばかなりわかりやすくなる問題を「今週の基本2題」に入れておくので、是非やってみてください。
◎【ミニ講座】(6) 三角数
規則性で学ぶ「数列」には様々なものがあります。
「等差数列」、「階差数列」、「三角数」、「平方数」、「フィボナッチ数列」などやらなければならないことは沢山ありますが、今回は「三角数」を取り上げたいと思います。
「三角数」とは、正三角形になるように点を等間隔に並べたときの点の総数ですが、1からnまでの自然数の和に等しくなります。
自然数の和には公式があります。
ガウスの子供の頃の逸話も有名ですね。
公式さえ覚えていれば三角数は計算で求めることができます。
ですが、ある程度は覚えておくと便利です。
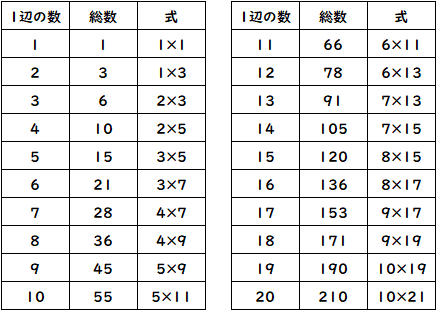
1~15までは比較的覚えやすいと思いますが、それ以降だと19番目の三角数が「190」で覚えやすいです。
他は無理して覚えなくても、覚えているものから増減すれば良いと思います。
表には「規則性」を重視した式を書いておきましたので参考にしてください。
表を見ながら自分なりに規則性を探してみると面白いですよ。
ちなみに「三角数」のお隣り同士の和は「平方数」になります。
これは図形的に説明できるので、知らなかった人は描いてみてくださいね。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
今週の基本2題速さ・規則性
難易度★★☆☆☆
- A,B,Cの3人が池のまわりを一定の速度で何周もします。
3人は同じ地点から同時にスタートし、
AとBは時計回り、Cは反時計回りに進みます。
池を1周するのにかかる時間はAが24分、Bが12分、Cが40分です。
3人が初めて池のまわりに等間隔に並ぶのはスタートしてから何分後ですか。
- 1番目から50番目までの三角数の和はいくつですか。