 濃度算とは
濃度算とは
濃度算とは、水溶液の濃度や溶媒・溶質の質量を求める問題です。
特に、濃度が異なる食塩水を混ぜる問題が多いです。
代表的な例としてはこのような問題。
例題1
10%の食塩水50gに20%の食塩水200gを加えると何%

他には混ぜたあとの水溶液から、
例題2
濃度5%の食塩水60gに濃度10%の食塩水を何gか混ぜ、

このように似たような問題でも解き方が異なるというのが濃度算の
今回はこれらの問題でもスムーズに解ける方法を解説していきます
それは、水溶液の濃度に関する公式です。
水溶液の濃度の公式
ここでは分かりやすいように、水溶液を食塩水とします。
食塩水の濃度というと、「食塩水に含まれる食塩の割合」を指しま
これは「割合の求め方」と「食塩水の意味」
ちなみに100をかけるのは、小数を百分率に変換するためです。

ただここで、『食塩水の量』が『食塩と水を合わせた量』
たとえば以下の問題の場合。
80gの水に食塩20gを溶かしたら濃度は何%か?

- 間違った例:20÷80×100=25%20÷80×100=
25% - 正しい例:20÷(20+80)×100=20%20÷(20+
80)×100=20%
水80gに対する食塩20gの割合は25%です。
しかし、食塩水の濃度は食塩水100g(食塩20g+水80g)
この濃度20%の食塩水は、「20%が食塩で残りの80%が水」
この点に関して、
ポイントとして、
- 水の量
- 食塩の量
- 食塩水の量
- 濃度

4つのうちどれか2つの値がわかれば、
では文章問題を解く前に、
例題1
濃度20%の食塩水150gに含まれる食塩は□g。
食塩水150gに対して食塩が20%なので、
150×20÷100=30150×20÷100=30となり、
例題2
濃度5%の食塩水160gに含まれる水は□g。
160gのうち5%、160×5÷100=8g160×5÷
ちなみに、食塩水の5%が食塩ということは残りの95%
例題3
17%の食塩水□gに含まれる食塩は10.2g。
「濃度=食塩の量÷食塩水の量」から、「食塩水の量=食塩の量÷

長方形の縦・横が濃度・
というわけで食塩水の量は、10.2÷17×100=60g10
濃度算の文章問題の解き方
では上で挙げた例題を用いて、
例題1
10%の食塩水50gに20%の食塩水200gを加えると何%

食塩水の濃度を計算するには、
混ぜたあとの食塩水の量・
食塩水の量の和:50+200=250(g)50+200=
濃度10%の食塩水50gは50×10÷100=550×10÷
食塩の量の和:5+40=45(g)5+40=45(g)
250gの食塩水のうち45gが食塩なので、濃度は45÷250
つづいてこちらの問題。
例題2
濃度5%の食塩水60gに濃度10%の食塩水を何gか混ぜ、

例題1と同様、濃度が違う食塩水を混ぜる問題ですが、
食塩水の2つの要素が分かっていれば他の要素を求めることができ
ここで便利なテクニックを紹介します。
前述しましたが、食塩水は縦・横を濃度・

これより、「5%の食塩水60g」と「10%の食塩水□g」

つまり、⇒の左右の面積が等しくなるように□
左右の図形を重ねたら以下のようになります。

図で表した部分の面積が等しくなればいいので、「?×2=60×
よって、答えは90gです。
複雑な割合の問題も図形の面積問題に変換できるわけです。
面積図を使う問題をもう一問見てみましょう。
例題3
濃度10%の食塩水200gに食塩を何gか混ぜ、濃度20%

このような問題でも、食塩を濃度100%
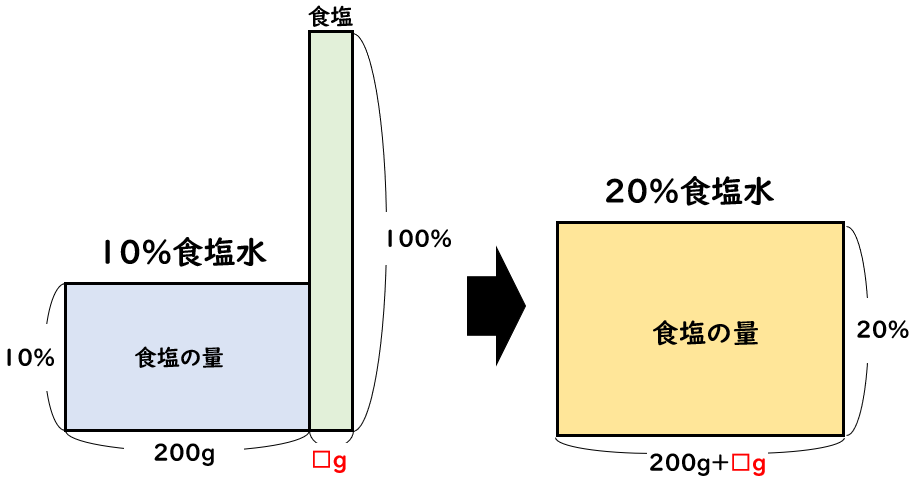

?×80=200×10?×80=200×10より、?
よって答えは25gです。
食塩水は4つのうち2つの要素が分かっていれば他の要素も単純な
もし簡単に求められないのであれば、面積図を用います。
大抵の濃度算の問題はこれだけ抑えておけば十分でしょう。
- 食塩水の4つの要素のうち2つを求める
- 2つの要素が簡単に求められない場合は面積図で求める









