植木算 中学算数 中学受験算数 令和

植木算とは

植木算とは、ある長さの道に一定間隔で木を植えたときの「植えた木の本数」や「道の長さ」、「木と木の間隔」などを求める文章問題です。

簡単な例としてはこのような問題。

植木算の例題1
30mの道のはしからはしまで一定の間隔で木を7本植えた。このとき木と木の間隔は何mか求めよ。

図を書いてみたらこのようになります。

30mの道を6等分しているので、30÷6＝530÷6＝5となり、答え5mです。

7本の木を植えているのに6で割らないといけないというのがややこしいですが、実際に図を書いてみたらそこまで難しくはないと思います。

そしてもう一つ代表的な問題の例が次のような問題。

植木算の例題2
電柱からバス停まで30m離れており、この間に5m間隔で木を植える場合、何本の木が必要になるか。

図に書いたらこのようになります。

30mを5m間隔に分割するには、30÷5＝630÷5＝6なので、6等分する必要があります。そして図を見たら分かると思いますが、6等分するには間に5本の植木が必要です。

前の問題では7本の木で道を6等分していましたが、この問題では両端に木を植えないので、5本の木で道が6等分できるのです。

いずれにしても等分する数と木の本数は合いませんし、直線の道に木を植える場合でも、両端に木を植えるか植えないかで考え方が違ってくるのが植木算の厄介な点です。

そしてもう一つ代表的な植木算の例を紹介します。これまでの直線の道ではなく池の周りなど巡回する道の植木算です。

植木算の例題3
池のまわりに5m間隔で6本の木を植えたら全部の木がちょうど等間隔になった。このとき池のまわりの全長を求めよ。

図に書いたらこのようになります。

6本の木で池が6等分に分割されており、それぞれの間隔が5mなので、6×5＝306×5＝30で池のまらりは30mです。

前の2つの例のどちらとも異なり、巡回する道の植木問題では「木の本数」と「等分する数」が等しくなります。

 

以上の3つの例が主な植木算のパターンです。

植木算は図を書けばそこまで難しくないのですが、状況によって木の本数と分割する数が変わってくるので、文章を読んだだけでは間違えやすいです。

公式で覚えるのではなく、問題に応じてその都度簡単な図を書いて整理するのが重要になります。

ちなみに植木算は「全体の長さ」に「一定間隔」でものを配置する問題なので、『道の植木の間隔』の他にも『竹の節の間隔』や『服のボタンの間隔』、『紐の結び目の間隔』、『勉強時間の休憩の間隔』など問題は様々なパターンが考えられます。

ただ、どんな問題でも解き方のポイントは同じです。

それぞれのパターンや解き方についてきちんと抑えていきましょう。

植木算を解く上でのポイント

まず、植木算には3つのパターンがあるということを抑えましょう。

それぞれ例題1、例題2、例題3に対応します。

これらを公式のように覚えて問題に応じて使い分けるという解き方もありますが、かえって混乱しやすいです。

簡単な図を書くくらいならそんなに時間はかからないと思うので、その都度図に書いて整理するのをオススメします。

ただし、木の本数が多い場合は時間がかかるので、そういう場合は小さい数に置き換えて公式を導きましょう。

たとえば「はしからはしまで木を100本植えた」という場合、道は何等分されているでしょうか。

100本の木を図に書くのは大変ですが、上のような図をイメージしたら3本の木で道が2等分、4本の木で道が3等分されるのは容易に分かると思います。

「3本だと2等分、4本だと3等分されるから『（木の本数-1）が分割する数』になる。つまり100本だと道は99等分される」

このように木の本数と間の数の関係が導けます。

 

では「両端をあけて木を200本植えた」という場合は道は何等分されているでしょうか。これも200本の木を図に書くのは大変ですが、上のような図をイメージしたら1本の木で道が2等分、2本の木で道が3等分されるのは容易に分かると思います。

「1本だと2等分、2本だと3等分されるから『（木の本数+1）が分割する数』になる。つまり200本だと道は201等分される」

このように木の本数と間の数の関係が導けます。

 

「池の外周に300本の木を植えた」という、巡回する道に木を植える場合でも同じように解いていきましょう。

「2本で2等分、3本で3等分されるから『木の本数が分割する数』になる。つまり300本だと道は300等分される」

このように木の本数と間の数の関係が導けます。

 

植木算で重要なのは、木の本数と等分の数を間違わないことです。これさえ完ぺきに抑えておけば、あとはよっぽど変則的な問題が出されない限りそこまで難しいことはないかと思います。

日暦算 中学算数 中学受験算数 令和

日暦算とは

日暦算とは、基準となる日の曜日からとある日の曜日を導く問題です。

たとえばこのような問題。

例題
2015年の5月20日は水曜日であるが2018年の3月29日は何曜日か。2016年がうるう年であることに注意して求めよ。

前提知識として『うるう年』や『月ごとの日数』などの最低限の教養が必要になります。

これらを知っていても解き慣れていなければ非常にややこしい問題なので、しっかりポイントを抑えておくのが重要です。

ただ慣れてしまえば問題のバリエーションは少ないので、そこまで怖い問題ではありません。

では日暦算のポイントと解き方について解説していきます。

日暦算を解くためのポイント

曜日は「月・火・水・木・金・土・日」の7個が繰り返されるため、7で割った余りから基準の曜日の何日後かが分かります。

これは「周期算」と同様の考え方なので合わせて抑えておくとよいでしょう。

具体的に例を見てみます。

例
とある日曜日の15日後の曜日は何曜日か？

「15÷7＝2あまり1」より、15日後は2週間と1日後となります。

つまり日曜日の1日後の曜日なので答えは月曜日です。

◯日後と曜日の対応を表にまとめると以下の通り。

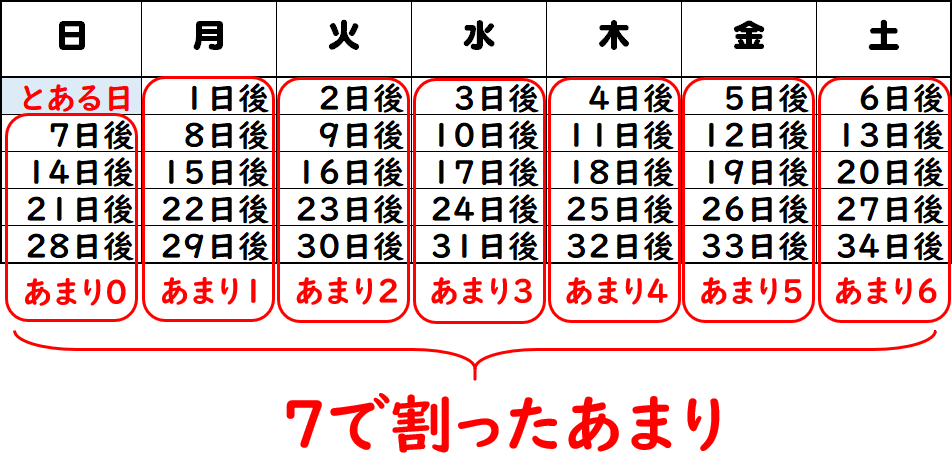
どんなに数字が大きくなっても7で割ったときのあまりから、基準の曜日からのズレが計算できます。

しかし、日暦算は「◯日後」というのが直接問われることはなく、だいたいが日付が与えられ、それを元に何日後かを導かないといけません。

そのために必要なのが以下の2つの知識です。

日暦算に必要な前提知識

 

1. 1年間の日数は平年が365日、うるう年が366日。
2. 平年の1月～12月の日数は「31、28、31、30、31，30，31，31，30，31，30，31」。『に2月・し4月・む6月・く9月・さむらい11月』以外が31日までと覚えるとよい。うるう年は2月29日が追加される。

うるう年は西暦で表した時の4の倍数の年。例外として100の倍数のうち400で割り切れない場合は平年。

例）

1，2000、2004、2008、2012・・・はうるう年

２，2400，2800，3200，・・・はうるう年だが、2100、2200、2300、2500・・・などは平年

うるう年かどうかは問題文で提示されていることが多いですが、一応知っておいたほうがよいです。

ではこれを用いて例題を解いていきましょう。

日暦算の解き方

例題1

ある年の1月1日は月曜日だった。3年後の1月1日は何曜日か。ただし、3年間の間にうるう年が1年だけ含まれるとする。

うるう年だと1年は366日ですが、それ以外は365日です。

なので1年後の同じ日付になるのはうるう年の2月29日を含むなら366日後、含まないなら365日後になります。

「日数」と「◯日後」というのを対応させるのは少し厄介ですが、一週間を考えるとイメージしやすいです。

一週間は7日ですが、一巡して次に同じ曜日になるのは7日後です。

これと同じように1ヶ月後の同じ日にちになるのはその月が30日までなら30日後、31日までなら31日後。

1年後の同じ日にちになるのは、2月29日を含むなら366日後、含まないのなら365日後、となるわけです。

では3年後の1月1日は何日後になるかを考えましょう。

1年だけうるう年があるので、この年は366日、ほかは365日です。つまり、366+365×2＝1096（日後）。

「1096÷7＝156あまり4」より、1月1日月曜日の156週間と4日後が3年後の1月1日にあたります。

月曜日の4日後の曜日なので金曜日が答え。

ちなみに「365÷7＝52あまり1」「366÷7＝52あまり2」より、1年後の同じ日付の曜日は2月29日を含まないなら1つ後の曜日、2月29日を含むなら2つ後の曜日になります。

今回はうるう年×1、平年×2なので、合計4つ後の曜日になっていますね。

覚えやすいのでこれをそのまま覚えておいてもよいでしょう。

• 「平年（365日後）」の1年後：1つ後の曜日
• 「うるう年（366日後）」の1年後：2つ後の曜日

例題2

ある年の4月27日は土曜日だった。その年の7月21日は何曜日か。

7月21日が4月27日の何日後かを考えます。

まずは各月の日数をおさらいしましょう。

「に・し・む・く・さむらい」の月以外は31日までなので、5月が31日まで、4月と6月は30日までです。

そして各月の最終日まで何日後かを考えると以下の通り。

• 「4月27日⇒4月30日」は3日後
• 「4月30日⇒5月31日」は31日後
• 「5月31日⇒6月30日」は30日後
• 「6月30日⇒7月21日」は21日後

これらを足すと3+31+30+21＝85より、7月21日は4月27日の85日後。

「85÷7＝12あまり1」となるので、12週間と1日後というのが分かりました。

つまり土曜日の1日後の曜日なので日曜日が答えです。

ちなみに、「◯日後」の計算の仕方ですが、『4月27日⇒7月27日』は91日後、7月21日はその6日前なので85日後、と考えることもできます。

例題3

2015年の8月19日は水曜日であるが2018年の3月29日は何曜日か。2016年がうるう年であることに注意して求めよ。

2018年3月29日が2015年8月19日の何日後かを考えましょう。

まず年を揃えます。

2015年8月19日の3年後、2018年8月19日は例題1と同じ要領でうるう年を考慮すると、366+365×2＝1096（日後）というのが分かります。

つぎに3月29日が8月19日の何日前かを求めましょう。

3月～7月の日数は順番に31日、30日、31日、30日、31日なので「8月19日⇒3月19日」は31+30+31+30+31＝153（日前）。3月29日はその10日後なので143日前。

1096日後の143日前は953日後。2018年3月29日は2015年8月19日の953日後ということです。

「953÷7＝136あまり1」より136週間と1日後なので水曜日の1日後の木曜日が答え。

 

日暦算は非常にややこしく難解ですが、問題のパターン自体はだいたい決まっているため、慣れてしまえば怖い問題ではありません。