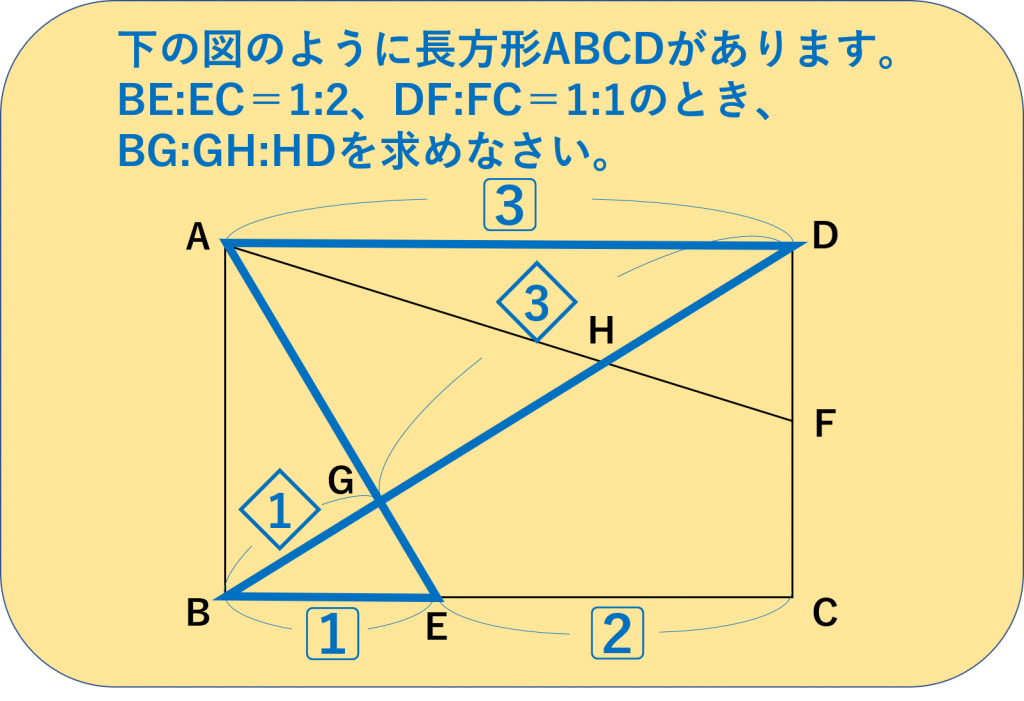
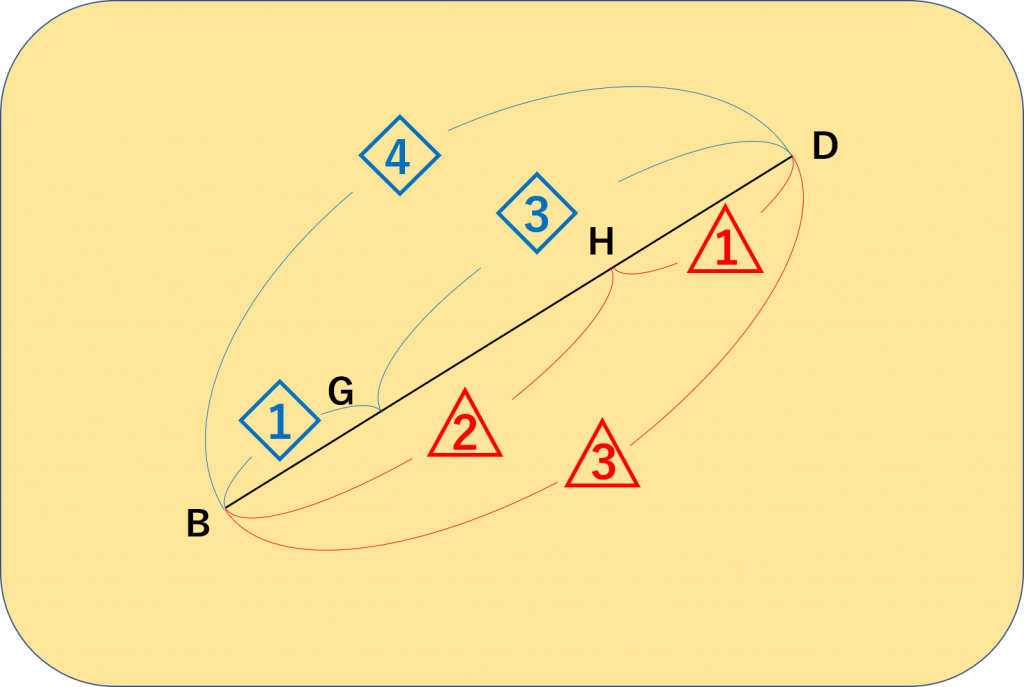
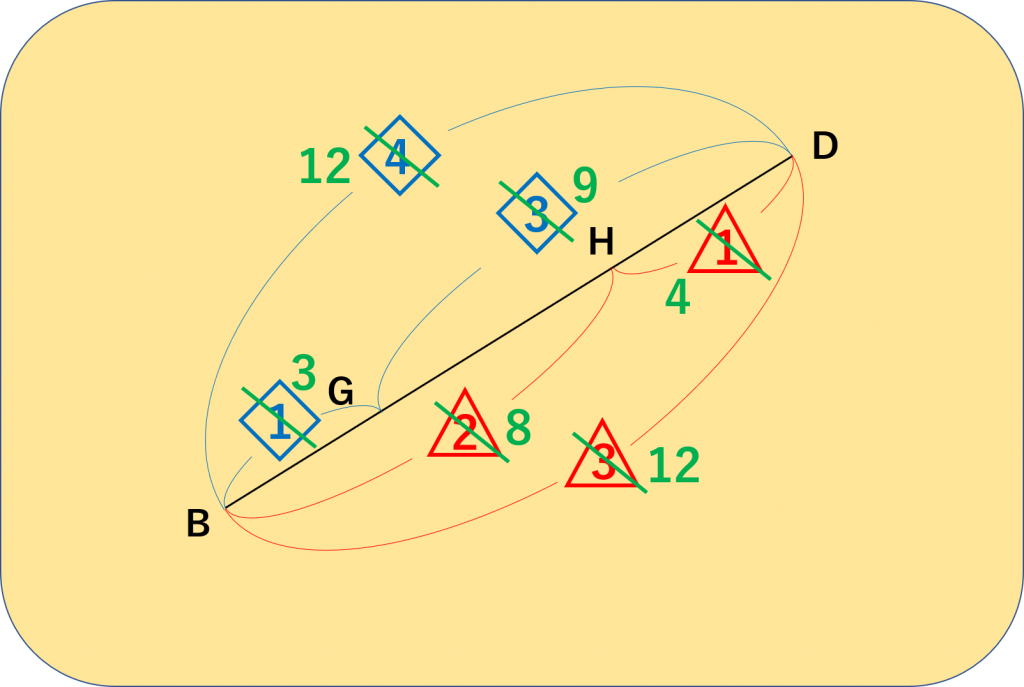
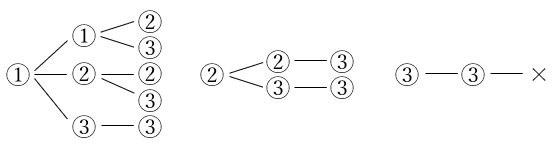
算数の単位の根本原理 国を愛する心はすごく大事

算数の単位の根本原理

算数の単位についてお話しいたします。

小学校の算数で習う単位にはいくつかの種類があります。

①長さの単位　㎞(キロメートル)/m(メートル)/㎝(センチメートル)/mm(ミリメートル)

②面積の単位　㎢(平方キロメートル)/ha(ヘクタール)/a(アール)/㎡(平方メートル)/㎠（平方センチ）

③体積の単位　㎥(立方メートル)/kL(キロリットル）/L(リットル)/dL(デシリットル)/mL(ミリリットル)/㎤（立方センチ）

④重さの単位　t（トン）/㎏（キログラム）/g（グラム）/mg（ミリグラム）

代表的な単位でもこれだけあるので、なかなか一度には覚えきれません。
丸暗記してもすぐに忘れてしまいます。

算数の単位を覚えるときの根本原理は以下の3点です。

①補助単位を覚える。
②面積の単位で出てくる㎠（平方センチ）の小さな2の意味を理解する
③体積の単位で出てくる㎤（立法センチ）の小さな3の意味を理解する

まずは①補助単位について説明します。

補助単位とは、単位の記号の前にある数です。
代表的な補助単位には、以下のようなものがあります。
k　＝キロ=1000倍
h　＝ヘクト=100倍
d　＝デシ=　1/10倍
C　＝センチ=1/100倍
m　=ミリ=1/1000倍

㎞は、キロが1000倍という意味なので、1mの1000倍となります。
ｍｍ（ミリメートル）は1ｍの１/1000倍です。
ha（ヘクタール）ということは、1aの100倍ということですし、
ｄⅬ（デシリットル）は1Ⅼの1/10ということになります。

この補助単位を覚えてしまえば、単位の意味が分かるので、
度忘れしてしまったときにも思い出すことができます。

単位が苦手な人は、まずは補助単位を覚えましょう。
次に②について説明します。

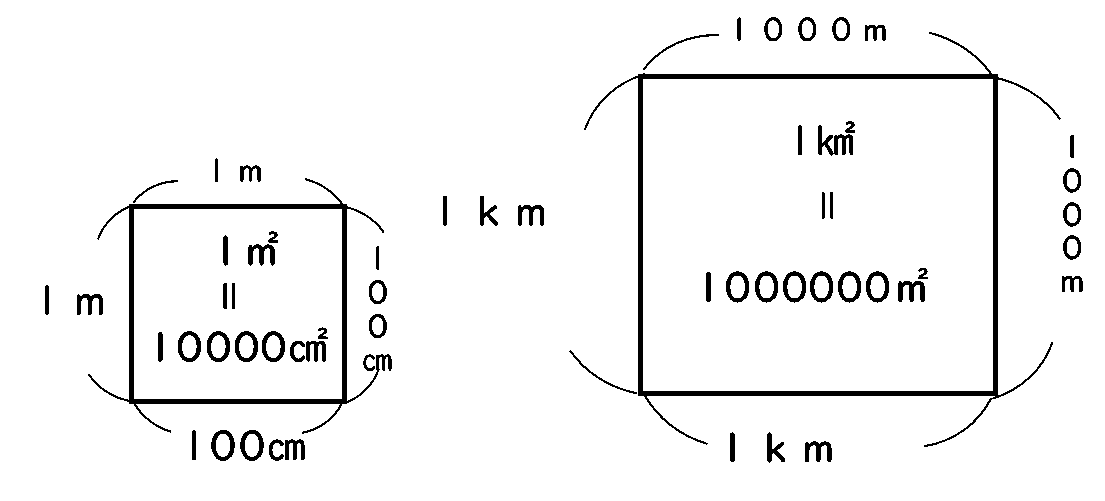
㎡や㎢の小さい2は縦×横で2個かけ算しているという意味です。
ですから、1㎢は1㎡の1000倍×1000倍=1000000倍になります。
また、1㎡は1㎠の100倍×100倍=10000倍になります。
㎢は㎡の1000倍ではないですし、㎡は㎠の100倍ではありません。

このような図をイメージして考えてください。

また、面積の単位でまぎらわしいのは、aとhaです。
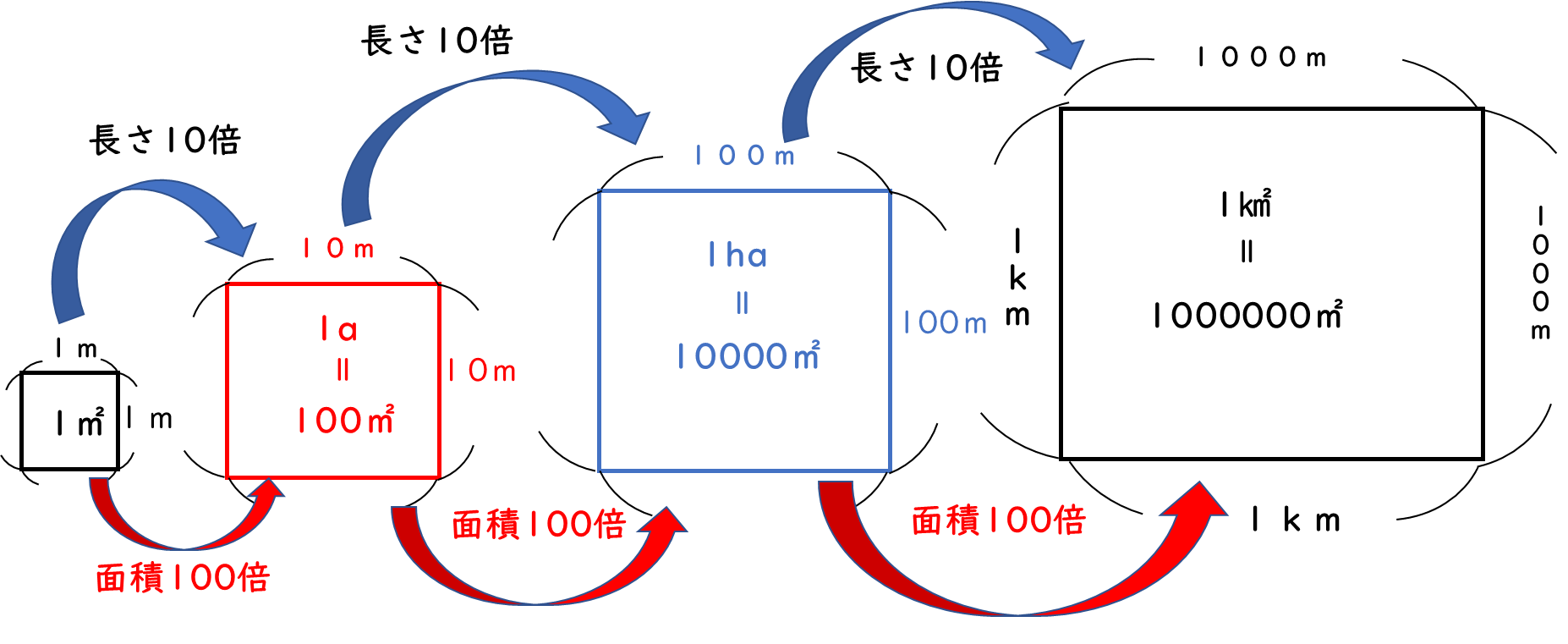
大きい面積の単位は㎡⇒a⇒ha⇒㎢と変化していきます。
これは次の規則に従っています。

A;長さは10倍ずつ増えてゆく
1倍(1m×1m)、10倍(10m×10m) 、100倍(100m×100m) 、1000倍(1000m×1000m）
B;面積は100倍ずつ増えてゆく
1倍、100倍、10000倍、1000000倍

上の図を自分で書いてみると、面積の増え方の根本原理がつかめます。
面積の大きさのイメージとして
㎡＝教卓
a＝教室
ha＝校庭
と考えておくと、およその広さがつかみやすくなります

最後に③について説明します。

体積の単位㎥や㎤の小さい3は、縦×横×高さで3個かけ算しているという意味です。
そうすると、長さが１倍、10倍、100倍となるとき、
以下の計算が成り立つので、体積は１倍、１０００倍、１０００００倍となります。

1㎤=1㎝×1㎝×1㎝
1L=10㎝×10㎝×10㎝=1000㎤
1㎥＝1m×1m×1m=100㎝×100㎝×100㎝＝1000000㎤

体積の大きさのイメージは納豆がどれくらいつまっているかで考えます。

1mL=1㎤＝納豆ひとつぶ
1dL=納豆パック（納豆１００つぶ）
1L=牛乳パック　（納豆10パックぶん、合計1000個）
1kL=家のお風呂（納豆100万個）

お風呂いっぱいの100万粒の納豆・・・。
ちょっと想像したくない、という人は、納豆を1㎤の小さなサイコロに置きかえてください。

【平面図形】見通しを立てて解き進めよう！ 守ろうわが国の領土

今回は「連比」を使った「相似」の典型題を解説します。
まずは次の問題を見てください。

この問題がスラスラ解けるなら、「相似」についての応用力はまずまずできていると考えていいでしょう。
受験ドクターの根本原理では実践編の110番に出てくる、超典型かつ超重要問題です。
この問題を解く上では、正しく方針が立てられているか、これが重要です。
今回のように、３つの部分の比が問われたときは、基本的に「連比」を使う以外の方法はあり得ません。
そもそも「比」というのは、２つのものを比べた数字なので、いきなり３つを比べるということはないのです。
ですから、BG:GH:HDを求めたければ、BD上で２組の比を見つけなければいけない、ということです。
うまく２組の比が見つけられれば、あとは「連比」をすればOKだな！と考えられていれば大丈夫です。
やみくもに問題を解き始めてもうまくいかないので、まずは解答までの見通しをつけるようにしましょう。

以上のように方針が立つなら、次に考えることは、この図の中で２組の相似形を見つける、ということです。
見つからなければ、補助線を引いて自分で作ることも考えなければいけません。
しかし、この図の場合はすでにちょうど良い相似形が２組ありますね？
それが見えますか？
ひとつはこれですね。

そして、もうひとつはこれです。

ついでに比も書き込んでしまいましたが、ここまで見えればゴールは目の前です。
BH:HDとBG:GDがわかったので、あとはこの２つを「連比」すれば、答えが出るはずです。

このときに、無理にひとつの図の中で処理しようとしない方が良いです。
面倒くさがらずに、BDだけ別に書き出して整理する方がミスは少なくなるはずです。
具体的にはこんな感じです。

ゴールまであと少しですね。
そう、あとは「連比」です！
前回もお伝えしたように、同じ長さのはずなのに、数字が違っている部分を探します。
今回はBDの部分がポイントですね！
青数字はBDが４となっていて、赤数字はBDが３となっています。
ということで、ここをそろえてあげれば、すべての数字が足したり引いたりできるようになります。

ということで、BG:GH:HD＝3:5:4となります。
いかかがですか？
きちんと求めることができたでしょうか？
今回の問題は、とても重要ですので、うまくできなかった場合は何度でも練習してください。
同じ問題で構いません。
手順や答えを完全に覚えてしまっていいので、むしろそこまで覚えてしまうことを目標に練習してください。

場合の数の裏技 同胞日本人に元気あげたい

場合の数の裏技

今回はタイトルにもあるように「場合の数」について書きたいと思います。

場合の数って、数え漏れによるおしい間違いが起きやすいですよね！

そんなミスが少しでも減ったらいいなと思い、裏技を紹介したいと思います。
今回この裏技を使う問題は「区別された数種類の複数ものから何個か選ぶときに何通りの選び方があるか」というパターンの問題です。
では、例を交えつつ説明していきます。

 

問題①

黒ペン2本、赤ペン2本、青ペン2本があります。この中から3本を選ぶとき何通りの選び方があるか求めなさい。

 

さて、どうでしょうか。黒－赤－赤や赤－赤－青と書き出していった子もいれば、同じ色のペンを2本選ぶ場合と、1本選ぶ場合で場合分けした子もいるのではないでしょうか。
どちらも間違いではありませんし、それで100発100中できていれば問題ありません。

 

では、「裏技」でやってみましょう！

 

この裏技でやることは2つだけです。

1つ目は、黒ペン、赤ペン、青ペンに番号をつけることです。
黒ペン＝①、赤ペン＝②、青ペン＝③のように。

2つ目は、その番号を背の順に並べることです。
※組み合わせの問題は重複してはいけないので大原則は背の順です。背の順に並べることで1－1－2と1－2－1などの重複を防ぐことができます。背の順とは、左から右に行くほど数値が大きくなるようにすることです。同じ数字はOKです。小さくなるのが絶対にNGです。

すると、

となり、7通りと分かります。

ではこのやり方を練習してみましょう。

 

問題②

黒ペン2本、赤ペン3本、青ペン3本があります。この中から3本を選ぶとき何通りの選び方があるか求めなさい。

 

 

どうでしょうか。では、答えです。

となり、9通りと分かります。

 

では、最後に1問です。数も増えますので、この問題ができれば完璧でしょう！
できなくても何回も練習してできるようになれば大丈夫です！

 

問題③

黒ペン2本、赤ペン3本、青ペン3本があります。この中から4本を選ぶとき何通りの選び方があるか求めなさい。

 

どうでしょうか。では、答えです。

となり、10通りと分かります。

合っていたでしょうか。合っていた子は自信をもってください。合っていなくてもしっかりと復習してできるようになれば「できるようになった」という結果は同じですから心配しないでください。