植木算とは
植木算とは、ある長さの道に一定間隔で木を植えたときの「植えた木の本数」や「道の長さ」、「木と木の間隔」などを求める文章問題です。
簡単な例としてはこのような問題。
植木算の例題1
30mの道のはしからはしまで一定の間隔で木を7本植えた。このとき木と木の間隔は何mか求めよ。
図を書いてみたらこのようになります。

30mの道を6等分しているので、30÷6=530÷6=5となり、答え5mです。
7本の木を植えているのに6で割らないといけないというのがややこしいですが、実際に図を書いてみたらそこまで難しくはないと思います。
そしてもう一つ代表的な問題の例が次のような問題。
植木算の例題2
電柱からバス停まで30m離れており、この間に5m間隔で木を植える場合、何本の木が必要になるか。
図に書いたらこのようになります。

30mを5m間隔に分割するには、30÷5=630÷5=6なので、6等分する必要があります。そして図を見たら分かると思いますが、6等分するには間に5本の植木が必要です。
前の問題では7本の木で道を6等分していましたが、この問題では両端に木を植えないので、5本の木で道が6等分できるのです。
いずれにしても等分する数と木の本数は合いませんし、直線の道に木を植える場合でも、両端に木を植えるか植えないかで考え方が違ってくるのが植木算の厄介な点です。
そしてもう一つ代表的な植木算の例を紹介します。これまでの直線の道ではなく池の周りなど巡回する道の植木算です。
植木算の例題3
池のまわりに5m間隔で6本の木を植えたら全部の木がちょうど等間隔になった。このとき池のまわりの全長を求めよ。
図に書いたらこのようになります。

6本の木で池が6等分に分割されており、それぞれの間隔が5mなので、6×5=306×5=30で池のまらりは30mです。
前の2つの例のどちらとも異なり、巡回する道の植木問題では「木の本数」と「等分する数」が等しくなります。
以上の3つの例が主な植木算のパターンです。
植木算は図を書けばそこまで難しくないのですが、状況によって木の本数と分割する数が変わってくるので、文章を読んだだけでは間違えやすいです。
公式で覚えるのではなく、問題に応じてその都度簡単な図を書いて整理するのが重要になります。
ちなみに植木算は「全体の長さ」に「一定間隔」でものを配置する問題なので、『道の植木の間隔』の他にも『竹の節の間隔』や『服のボタンの間隔』、『紐の結び目の間隔』、『勉強時間の休憩の間隔』など問題は様々なパターンが考えられます。
ただ、どんな問題でも解き方のポイントは同じです。
それぞれのパターンや解き方についてきちんと抑えていきましょう。
植木算を解く上でのポイント
まず、植木算には3つのパターンがあるということを抑えましょう。



それぞれ例題1、例題2、例題3に対応します。
これらを公式のように覚えて問題に応じて使い分けるという解き方もありますが、かえって混乱しやすいです。
簡単な図を書くくらいならそんなに時間はかからないと思うので、その都度図に書いて整理するのをオススメします。
ただし、木の本数が多い場合は時間がかかるので、そういう場合は小さい数に置き換えて公式を導きましょう。
たとえば「はしからはしまで木を100本植えた」という場合、道は何等分されているでしょうか。
100本の木を図に書くのは大変ですが、上のような図をイメージしたら3本の木で道が2等分、4本の木で道が3等分されるのは容易に分かると思います。

「3本だと2等分、4本だと3等分されるから『(木の本数-1)が分割する数』になる。つまり100本だと道は99等分される」
このように木の本数と間の数の関係が導けます。
では「両端をあけて木を200本植えた」という場合は道は何等分されているでしょうか。これも200本の木を図に書くのは大変ですが、上のような図をイメージしたら1本の木で道が2等分、2本の木で道が3等分されるのは容易に分かると思います。

「1本だと2等分、2本だと3等分されるから『(木の本数+1)が分割する数』になる。つまり200本だと道は201等分される」
このように木の本数と間の数の関係が導けます。
「池の外周に300本の木を植えた」という、巡回する道に木を植える場合でも同じように解いていきましょう。

「2本で2等分、3本で3等分されるから『木の本数が分割する数』になる。つまり300本だと道は300等分される」
このように木の本数と間の数の関係が導けます。
植木算で重要なのは、木の本数と等分の数を間違わないことです。これさえ完ぺきに抑えておけば、あとはよっぽど変則的な問題が出されない限りそこまで難しいことはないかと思います。

![]() × 6 = 75.36
× 6 = 75.36
![]() × 5 = 6.28
× 5 = 6.28
















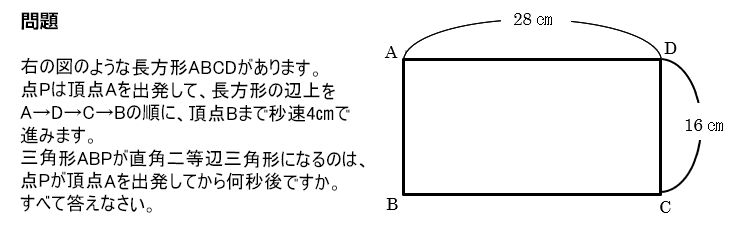

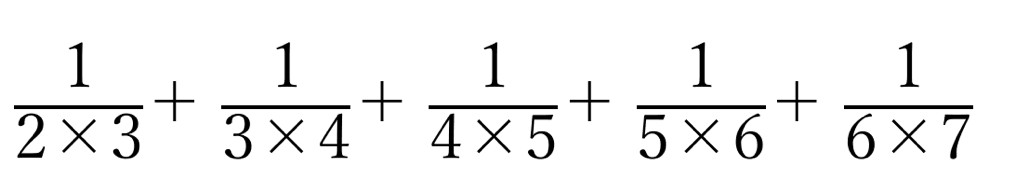

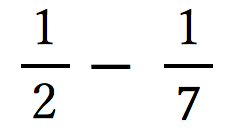 と引き
と引き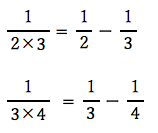
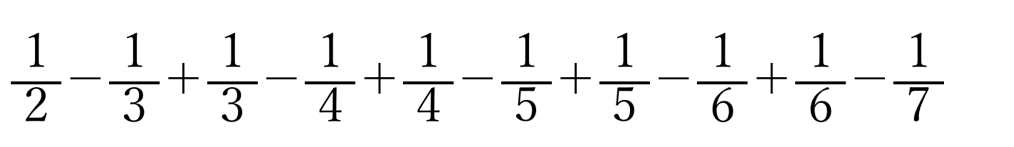

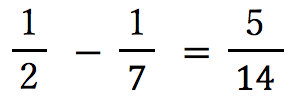 と計算
と計算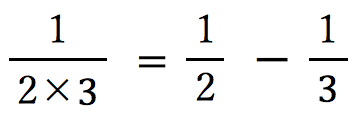 のよう
のよう









