本日は、無償学習塾の学習指導に参加しました。高校1年生の生徒さんに、数学の「一次方程式の応用」(中学数学の復習)を解説しました。
(例題)
箱とボールがそれぞれいくつかあり、ボールを箱に入れていく。
1箱につきボールを6個ずつ入れた場合、全ての箱にボールが6個ずつ入り、どの箱にも入れていないボールは20個になった。
また、1箱につきボールを7個ずつ入れた場合、全てのボールを箱に入れることができ、ボールが1つも入っていない箱が8箱、ボールが3個入った箱が1箱になった。
箱は全部で何箱あるか、求めなさい。
はじめに、全体の箱数をxとします。それぞれのボールの入れ方より、全体のボール数をxを用いた式で表します。一例として、下の図のようにして考え、このときのxの値を求めていきます。
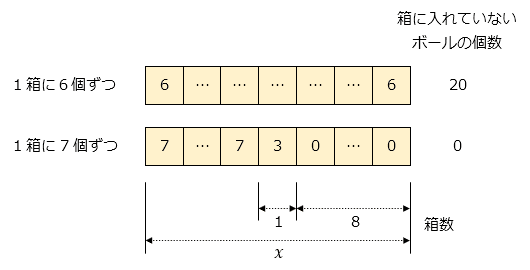
・1箱につきボールを6個ずつ入れた場合
x箱にボールが6個ずつ入っており、箱に入れていないボールが20個あることから、
全体のボール数は (6x+20)個 と表されます。 … ①
・1箱につきボールを7個ずつ入れた場合
図より、ボールが7個入っている箱は (x-9)箱 あります。
(x-9)箱にボールが7個ずつ入っており、他の1箱にボールが3個入っていることから、
全体のボール数は 7(x-9)+3
したがって、(7x-60)個 と表されます。 … ②
①②は、それぞれボールの入れ方が違うだけで、全体のボール数は同じであるから、6x+20=7x-60 の関係が成り立ちます。これを解くと、x=80
したがって、箱は全部で80箱あります。 … [答]
数量関係を把握する際に、図や数直線を利用すると全体像が見えやすくなりますので、有効活用して解いてほしいです。
この日の夜に満月が見えました。4月の満月は、「ピンクムーン」と呼ばれています。月の色がピンク色に染まるわけではなく、アメリカの先住民が春に咲く花の色にちなんで名付けたのが始まりとされています。

出典
朝日新聞 4月の満月は「ピンクムーン」、今夜から未明に 都心の空に明るい月
(例題)
箱とボールがそれぞれいくつかあり、ボールを箱に入れていく。
1箱につきボールを6個ずつ入れた場合、全ての箱にボールが6個ずつ入り、どの箱にも入れていないボールは20個になった。
また、1箱につきボールを7個ずつ入れた場合、全てのボールを箱に入れることができ、ボールが1つも入っていない箱が8箱、ボールが3個入った箱が1箱になった。
箱は全部で何箱あるか、求めなさい。
はじめに、全体の箱数をxとします。それぞれのボールの入れ方より、全体のボール数をxを用いた式で表します。一例として、下の図のようにして考え、このときのxの値を求めていきます。

・1箱につきボールを6個ずつ入れた場合
x箱にボールが6個ずつ入っており、箱に入れていないボールが20個あることから、
全体のボール数は (6x+20)個 と表されます。 … ①
・1箱につきボールを7個ずつ入れた場合
図より、ボールが7個入っている箱は (x-9)箱 あります。
(x-9)箱にボールが7個ずつ入っており、他の1箱にボールが3個入っていることから、
全体のボール数は 7(x-9)+3
したがって、(7x-60)個 と表されます。 … ②
①②は、それぞれボールの入れ方が違うだけで、全体のボール数は同じであるから、6x+20=7x-60 の関係が成り立ちます。これを解くと、x=80
したがって、箱は全部で80箱あります。 … [答]
数量関係を把握する際に、図や数直線を利用すると全体像が見えやすくなりますので、有効活用して解いてほしいです。
この日の夜に満月が見えました。4月の満月は、「ピンクムーン」と呼ばれています。月の色がピンク色に染まるわけではなく、アメリカの先住民が春に咲く花の色にちなんで名付けたのが始まりとされています。

出典
朝日新聞 4月の満月は「ピンクムーン」、今夜から未明に 都心の空に明るい月















 ● AVERAGE関数
数式:AVERAGE(数値1, [数値2], …)
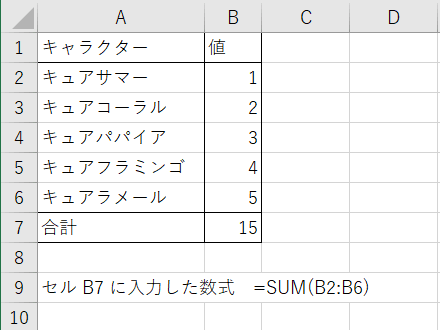
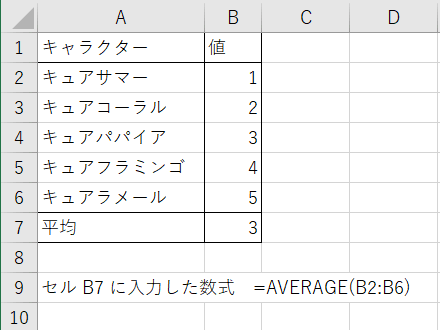
数値の平均値を求める関数です。例えば、次のように連続したセルB2~B6(セルB2, B3, B4, B5, B6)の各値を平均したい場合は、その値を表示するセルに「=AVERAGE(B2:B6)」と入力します。平均対象となるセルに数値型ではない値(仮名や空欄など)が入力されている場合は、そのセルの値は0扱いとなります。
● AVERAGE関数
数式:AVERAGE(数値1, [数値2], …)
数値の平均値を求める関数です。例えば、次のように連続したセルB2~B6(セルB2, B3, B4, B5, B6)の各値を平均したい場合は、その値を表示するセルに「=AVERAGE(B2:B6)」と入力します。平均対象となるセルに数値型ではない値(仮名や空欄など)が入力されている場合は、そのセルの値は0扱いとなります。
 ● IF関数
数式:IF(論理式, [式が真の場合], [式が偽の場合])
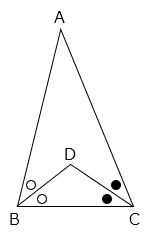
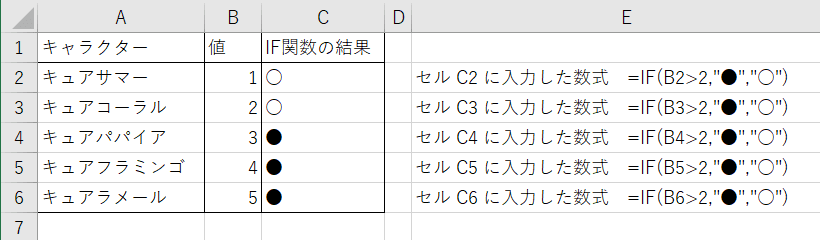
条件に応じて、セルに適用する式を指定する関数です。「論理式」の内容が真(はい)の場合は「式が真の場合」の式が、偽(いいえ)の場合は「式が偽の場合」の式が適用されます。次の例では、各キャラクターの値が2よりも大きい場合は●を、そうでない場合は○を表示しています。
● IF関数
数式:IF(論理式, [式が真の場合], [式が偽の場合])
条件に応じて、セルに適用する式を指定する関数です。「論理式」の内容が真(はい)の場合は「式が真の場合」の式が、偽(いいえ)の場合は「式が偽の場合」の式が適用されます。次の例では、各キャラクターの値が2よりも大きい場合は●を、そうでない場合は○を表示しています。
 ● ROUND関数
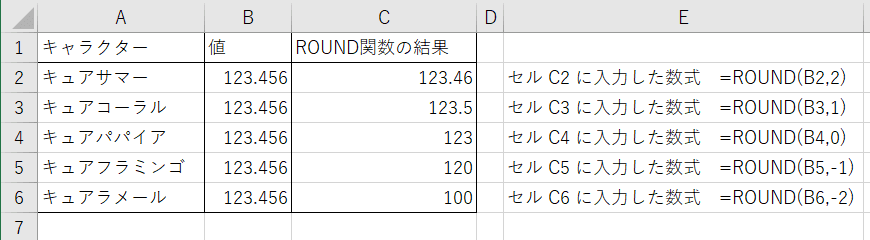
数式:ROUND([数値], [桁数])
四捨五入して指定の桁数まで求める関数です。「桁数」と四捨五入後の桁の関係は、次の通りです。
● ROUND関数
数式:ROUND([数値], [桁数])
四捨五入して指定の桁数まで求める関数です。「桁数」と四捨五入後の桁の関係は、次の通りです。
 秋田市(秋田地方気象台)では、11月26日に初雪が観測されました。これは、平年よりも11日、昨年よりも16日遅いとのことです。冬が本格化してきましたが、新型コロナの感染予防を継続し、寒さ対策も行って参ります。
出典
秋田市(秋田地方気象台)では、11月26日に初雪が観測されました。これは、平年よりも11日、昨年よりも16日遅いとのことです。冬が本格化してきましたが、新型コロナの感染予防を継続し、寒さ対策も行って参ります。
出典