数学のアート

ウィキペディア参照

 

私たちが"数字"を意識するのは、経済、日々の暮らしのお金の計算とか、お仕事上の時間に追われる場合とか、お買い物の損得勘定等々の様々な計算程度で、何時も（日常）はその程度のモノだと思うのです(＾◇＾)


数式となるとせいぜい、小学生の後半でピタゴラスの定理を教えられて、おぼろげながら三角形の不思議を思い出す程度なのかもしれません。


義務教育を終えるまで数字のお勉強では、私たちは解析学・代数学・幾何学のある事を教わった事になります。


それらはみんな、自分にとって苦手な数字の世界でした。


今では解析はというと、物事の、巨視的・微視的な数字の見方のイメージで、代数とは数字と四則演算の基本的な発想とそれ以上での代数とは、数字の不思議な世界の印象、幾何学なら図形や次元との数字の関係のイメージ（？）という大雑把な気持ちが数式にはあります。


という事で義務教育終了後の人生では、何かを比べる時くらいにしか数字は、私たちの生活では登場しない様な雰囲気ではないでしょうか・・・？


ところが数字には、面白い色々な秘密が隠されていました・・・。


数字と記号を用いれば、色々な事がイメージできます。


その中には、芸術に通じる美しさも存在している。


数式には、美すら存在しているという事です。


その事については、数学に今までの苦手さを忘れて、判らぬまでもある程度チョッピリ頑張ってみれば、ホウホウ、ナルホドなどと数字・数式の美しさの一端に、感動できるかもしれません。


この感動が、鮮明な方たちなほど、きっと数学に愛された人々なのでしょう。


その様な数学の先生から良く聴かされるお話が、オイラーの等式だと思います。





eはネイピア数。この数字が不思議なところは、・・・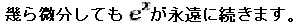





つまり、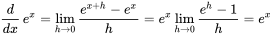



（ｘで微分＝ｈを極力小さくして引き算しても変わらない）


そして、 i は虚数。

 

i × i ＝ -1。


また、πは円周率。


これらはそれぞれ、解析学・代数学・幾何学で登場する数字で、それ等が0と1で数式になる。


iやπの虚数・無理数が、この様な式になった時、0と1で繋がってしまう・・・。


これが数式の美しさを表現しているという事です。


数学を愛している人々には、ソコに美を感じる様です。


オイラーは生前、息をするように計算していたと言う逸話を残した、天才だったそうです。


超有名な大天才数学者ガウスは、この公式を観て感動できない人には数学のセンスは、哀しいかな無いでしょうとさへ言わしめたそうです。


数学にはホトホト縁がなかった我人生(>_<)でも世の中には、想像も出来ない様な発想で、驚く程の世の中の秘密を暴露するかの様な人々が、数学で名を残してきました。


オイラーの等式には、解析学と代数学・幾何学が絶妙に融合されているという事が実感できるところが偉大なのだそうです。


それには先ず、マクローリン展開から話が始まります。





このkを無限に続けて計算すれば、・・・





この右辺の式と虚数の性質を組み合わせて、オイラーの公式に当てはめます。


ちなみにオイラーの公式は、・・・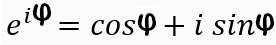





この公式の意味は縦軸に虚数、横軸に実数のグラフに単位円を描いたときに・・・





と表されます。


φ＝πとなった時に、オイラーの等式が成立すると・・・。


上述のグラフは曲形式で記された方式で、詳細はド・モアブルの定理で、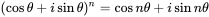





が成立する事が判っています。


これは正に、指数と周期の関係を数字で表現された事になります。
(その詳細はウィキペディアに委ねますm(_ _)m)


数字と記号で、自然の現象の美しさや不思議をヒトは知る事になりました。


そんな感じのするお話なので、日記にしておきます。