まずは大問1の計算だよ。基本が出来なきゃ応用なんて出来ないし、試合では勝てませんからね
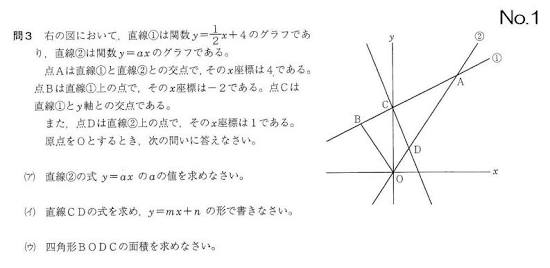
画像はよく出る関数の入試問題。共通テストに必ず出る「一次関数と比例」です
数学は、文章で読むより数式やグラフのほうが圧倒的カンタンに出来ています。まず問題文にそって、数字や文字そして式をグラフ上に書き込んでいきます。問題文とグラフと交互にながめながら考えるのはタイヘンだから。グラフに書き込んでおけばラクだし速く解けます
問題文を読みながらグラフに書き込んでしまいましょう
[関数の基本](↓自信がなきゃ書け!)
x軸とy軸のグラフでは、ひとつの点をx座標とy座標ふたつの座標(x,y)で表します
直線のグラフは一次関数★です
y=ax+b 、aは傾(かたむ)き 、bは切片(せっぺん)
原点(0,0)を通る直線のグラフは比例★です
y=ax 、aは傾(かたむ)き 、原点でy=0なのでbもゼロです
直線(1)や直線CDは一次関数。y=ax+bの形をとります
直線(2)や直線BOは原点を通る直線なので比例。y=axの形をとります
ここで使うxやyは変わる数、変数です
ここで使ったaやbには定まった数、定数が入ります
[解説]
(ア)直線(2)の式 y=axのaの値(あたい)を求めなさい。
直線(2)だけ鉛筆でたどってみましょう。点Aを通っていますね
数学は暗記の少ない教科ですから手がかりは問題文に書いてあります
点Aの座標(x,y)が問題文を読めばわかるはず
「点Aはは直線(1)と直線(2)との交点で、そのx座標は4である。」
ありました。座標(x,y)はx座標とy座標がありますから、x=4なら残ったy座標を求めればいいわけです
計算するには式が必要です。点Aは直線(1)と直線(2)との交点ですから、直線(1)y=(1/2)x+4が使えます。式と数字がわかりました。x=4を、式のx部分に代入します
y=(1/2)×4+4=6、点Aの座標は(4,6)です。グラフに書き込んでおきます
問いのゴールを確認します!★
直線(2)の式 y=axのaの値を求めなさいと書いてありますね
点A(4,6)を、 y=axのxとyの部分に代入です
6=a×4 → a×4=6 → a=6/4 → a=3/2
問題が続く場合、先に出した解はたいてい後で使います。わたしなら、直線(2)のところにy=(3/2)xも書き込んでおきます。式の形がいいですね。計算で式と座標(x,y)を使いますから
(ィ)直線CDの式を求め、y=mx+nの形で書きなさい。
直線CDだけ鉛筆でたどってみます。点Cと点Dを通ってますね(当たり前だ)
問題文から点Cと点Dを探します
「点Cは直線(1)とy軸との交点である。」
グラフとy軸との交点は切片のことです。切片はy=ax+bのbのことですね
直線(1)はy=(1/2)x+4ですから、b=4です
y軸はグラフのたて軸ですから、y座標だけ変わります。ここでは切片b=y=4です。
y軸はグラフのたて軸ですから、横軸のx座標は変わりません。y軸上で常にx=0です★
点C(0,4)がわかりました。わかったら、すぐグラフに書き込みます
点Dがまだです。「点Dは直線(2)上の点で、そのx座標は1である。」
代入したいのですがx座標だけでは解は出せません。じゃy座標を求めよう!
直線(2)y=(3/2)xに、x=1を代入します。y=(3/2)×1 → y=3/2
点Dの座標は(1,3/2)です。忘れずグラフに書き込みます
問いのゴールを確認します!★
直線CDの式を求め、y=mx+nの形で書きなさいとあります
点C(0,4)と点D(1,3/2)がわかっています。点Cはy軸上の点ですからやっぱり切片です
ここではb=n=4、直線CDはy=mx+4までわかります
式と数字がわかりました。点Dのx=1,y=3/2を、式のxとyの部分にそれぞれ代入します
点D(1,3/2) → 3/2=a×1+4 → a×1+4=3/2 → a×1=(3/2)-4 → a×1=-(5/2) → a=-(5/2)
ゴールは、直線CDの式を求め、y=mx+nの形で書きなさいでした
y=-(5/2) x+4
直線CDは右下がりのグラフですから、傾きaはちゃんとマイナスになっていますよね★
ふぅ疲れた。数学を文章で説明すんのシンドい。でもあなたがやるのは式と数字を書いていくことだけです。式に数字を代入していく繰り返しをですから慣れりゃカンタンです。初めの小問ふたつは確認さえできればそれだけで解けちゃいますから、みんな覚えてね
続きます(藤田)
画像はよく出る関数の入試問題。共通テストに必ず出る「一次関数と比例」です
数学は、文章で読むより数式やグラフのほうが圧倒的カンタンに出来ています。まず問題文にそって、数字や文字そして式をグラフ上に書き込んでいきます。問題文とグラフと交互にながめながら考えるのはタイヘンだから。グラフに書き込んでおけばラクだし速く解けます
問題文を読みながらグラフに書き込んでしまいましょう
[関数の基本](↓自信がなきゃ書け!)
x軸とy軸のグラフでは、ひとつの点をx座標とy座標ふたつの座標(x,y)で表します
直線のグラフは一次関数★です
y=ax+b 、aは傾(かたむ)き 、bは切片(せっぺん)
原点(0,0)を通る直線のグラフは比例★です
y=ax 、aは傾(かたむ)き 、原点でy=0なのでbもゼロです
直線(1)や直線CDは一次関数。y=ax+bの形をとります
直線(2)や直線BOは原点を通る直線なので比例。y=axの形をとります
ここで使うxやyは変わる数、変数です
ここで使ったaやbには定まった数、定数が入ります
[解説]
(ア)直線(2)の式 y=axのaの値(あたい)を求めなさい。
直線(2)だけ鉛筆でたどってみましょう。点Aを通っていますね
数学は暗記の少ない教科ですから手がかりは問題文に書いてあります
点Aの座標(x,y)が問題文を読めばわかるはず
「点Aはは直線(1)と直線(2)との交点で、そのx座標は4である。」
ありました。座標(x,y)はx座標とy座標がありますから、x=4なら残ったy座標を求めればいいわけです
計算するには式が必要です。点Aは直線(1)と直線(2)との交点ですから、直線(1)y=(1/2)x+4が使えます。式と数字がわかりました。x=4を、式のx部分に代入します
y=(1/2)×4+4=6、点Aの座標は(4,6)です。グラフに書き込んでおきます
問いのゴールを確認します!★
直線(2)の式 y=axのaの値を求めなさいと書いてありますね
点A(4,6)を、 y=axのxとyの部分に代入です
6=a×4 → a×4=6 → a=6/4 → a=3/2
問題が続く場合、先に出した解はたいてい後で使います。わたしなら、直線(2)のところにy=(3/2)xも書き込んでおきます。式の形がいいですね。計算で式と座標(x,y)を使いますから
(ィ)直線CDの式を求め、y=mx+nの形で書きなさい。
直線CDだけ鉛筆でたどってみます。点Cと点Dを通ってますね(当たり前だ)
問題文から点Cと点Dを探します
「点Cは直線(1)とy軸との交点である。」
グラフとy軸との交点は切片のことです。切片はy=ax+bのbのことですね
直線(1)はy=(1/2)x+4ですから、b=4です
y軸はグラフのたて軸ですから、y座標だけ変わります。ここでは切片b=y=4です。
y軸はグラフのたて軸ですから、横軸のx座標は変わりません。y軸上で常にx=0です★
点C(0,4)がわかりました。わかったら、すぐグラフに書き込みます
点Dがまだです。「点Dは直線(2)上の点で、そのx座標は1である。」
代入したいのですがx座標だけでは解は出せません。じゃy座標を求めよう!
直線(2)y=(3/2)xに、x=1を代入します。y=(3/2)×1 → y=3/2
点Dの座標は(1,3/2)です。忘れずグラフに書き込みます
問いのゴールを確認します!★
直線CDの式を求め、y=mx+nの形で書きなさいとあります
点C(0,4)と点D(1,3/2)がわかっています。点Cはy軸上の点ですからやっぱり切片です
ここではb=n=4、直線CDはy=mx+4までわかります
式と数字がわかりました。点Dのx=1,y=3/2を、式のxとyの部分にそれぞれ代入します
点D(1,3/2) → 3/2=a×1+4 → a×1+4=3/2 → a×1=(3/2)-4 → a×1=-(5/2) → a=-(5/2)
ゴールは、直線CDの式を求め、y=mx+nの形で書きなさいでした
y=-(5/2) x+4
直線CDは右下がりのグラフですから、傾きaはちゃんとマイナスになっていますよね★
ふぅ疲れた。数学を文章で説明すんのシンドい。でもあなたがやるのは式と数字を書いていくことだけです。式に数字を代入していく繰り返しをですから慣れりゃカンタンです。初めの小問ふたつは確認さえできればそれだけで解けちゃいますから、みんな覚えてね
続きます(藤田)





















