[問題]
熊本県中学校数学教育研究会編「数学の友1年」啓林館版より。単元"角柱、円柱の表面積"のP.79[3]です。一部変更。
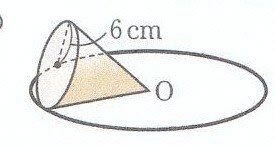
図のように、底面の半径が6cmの円錐を、頂点Oを中心として平面上で転がしたところ、もとの位置にもどるのに、円錐は3回転した。次の問いに答えなさい。
(1)円錐の母線の長さを求めなさい。
(2)円錐の表面積を求めなさい。
[接(せっ)した図形のルール]
"接した線分は、それぞれおなじ長さです。"
当たり前のことですが、なかなか気がついてはもらえません。数学が、理解できないナゾのルールでできていると思い込んでいるのかもしれない。数学は、"当たり前のルール"をどんな場合でも使えるようていねいに説明しているだけなのです。
[立体のルール]
角柱、円柱、角すい、円すい、は「立体」です。立体の問題なら、「体積」と「表面積」。問題文からまず、"なにを求めるか"を確認します。たいてい、問題文の最後に書かれています。
「表面積」は、cm^2(平方センチメートル)。2乗=「平方」のこと。たとえば、"平方根√7"は"2乗(平方)すると7になる数"のことですね。たて×横や一辺×一辺のように2回かけます。⇒「立体の表面積」は、面積ですから「展開図」を描いて平面に分けます。⇒円すいなら、「底面の円と側面のおうぎ形」を描きます。
図形問題は、文で書かれた条件を図に置きかえ、よりかんたんに理解や説明するトレーニングなのです。
図形問題はなんのため?|熊本県公立高校後期試験
[円の面積と円周のルール]
円の公式は、「円の面積」と。「円周」です。単位もつければ、まちがえません。
円の面積(cm^2) = πr^2
円周の長さ(cm) = 2πr
[底面と側面のルール]
(1)では、「円すいの母線の長さを求めよ」と問うています。「母線」とは、"回転体の側面を作る線分"のこと。⇒円すいの側面はおうぎ形。つまり「おうぎ形の半径」のことですね。
図で確認!円すいの底面と大きな円の円周は、"接(せっ)しながら"3回転しています。⇒大きな円の円周と円すいの底面の3回転分は、"おなじ長さ"です。おなじ長さの部分を、図で指して確認をします。
円すいの底面の円周 : 2πr = 2π × 6 = 12π (cm)
大きな円の円周 :
2π × 母線 = 12π × 3(回転)
母線 = 18(cm)
ルールさえわかれば、あとの計算はこんなにかんたん。
(2)へ続きます。(塾長)
図形問題はなんのため?|熊本県公立高校後期試験
熊本県中学校数学教育研究会編「数学の友1年」啓林館版より。単元"角柱、円柱の表面積"のP.79[3]です。一部変更。
図のように、底面の半径が6cmの円錐を、頂点Oを中心として平面上で転がしたところ、もとの位置にもどるのに、円錐は3回転した。次の問いに答えなさい。
(1)円錐の母線の長さを求めなさい。
(2)円錐の表面積を求めなさい。
[接(せっ)した図形のルール]
"接した線分は、それぞれおなじ長さです。"
当たり前のことですが、なかなか気がついてはもらえません。数学が、理解できないナゾのルールでできていると思い込んでいるのかもしれない。数学は、"当たり前のルール"をどんな場合でも使えるようていねいに説明しているだけなのです。
[立体のルール]
角柱、円柱、角すい、円すい、は「立体」です。立体の問題なら、「体積」と「表面積」。問題文からまず、"なにを求めるか"を確認します。たいてい、問題文の最後に書かれています。
「表面積」は、cm^2(平方センチメートル)。2乗=「平方」のこと。たとえば、"平方根√7"は"2乗(平方)すると7になる数"のことですね。たて×横や一辺×一辺のように2回かけます。⇒「立体の表面積」は、面積ですから「展開図」を描いて平面に分けます。⇒円すいなら、「底面の円と側面のおうぎ形」を描きます。
図形問題は、文で書かれた条件を図に置きかえ、よりかんたんに理解や説明するトレーニングなのです。
図形問題はなんのため?|熊本県公立高校後期試験
[円の面積と円周のルール]
円の公式は、「円の面積」と。「円周」です。単位もつければ、まちがえません。
円の面積(cm^2) = πr^2
円周の長さ(cm) = 2πr
[底面と側面のルール]
(1)では、「円すいの母線の長さを求めよ」と問うています。「母線」とは、"回転体の側面を作る線分"のこと。⇒円すいの側面はおうぎ形。つまり「おうぎ形の半径」のことですね。
図で確認!円すいの底面と大きな円の円周は、"接(せっ)しながら"3回転しています。⇒大きな円の円周と円すいの底面の3回転分は、"おなじ長さ"です。おなじ長さの部分を、図で指して確認をします。
円すいの底面の円周 : 2πr = 2π × 6 = 12π (cm)
大きな円の円周 :
2π × 母線 = 12π × 3(回転)
母線 = 18(cm)
ルールさえわかれば、あとの計算はこんなにかんたん。
(2)へ続きます。(塾長)
図形問題はなんのため?|熊本県公立高校後期試験





















