理科です。理工系の仕事に就(つ)く気ないし、なんの役に立つのかわかんない。そんなあなた。学校の受験用教材を使いましょう。図の多い単元からノートに図を写します。暗記は図が一番アタマに残りやすいからです。入試でもその図がそのまま出ますからおトクですよ。植物・動物・からだのつくり・気象それに実験や観察が図の多い単元ですね。受験用教材には図で解く問題だけまとめたページもあります
理科は図で理解することの多い教科です
次のオススメはグラフの問題。グラフの見方は社会にも数学にも応用がききます。なにより仕事に直結します。えー服の販売やるのに関係ないよー。ずっと目の前のお客さんだけが相手なら関係ないかもね。あなたが経験を積み店全体で利益を出すとなるとグラフを使わないわけにはいきません。年間を通して一定の利益を上げるにはカンは当たりはずれが大きいから。社長は給料が払えません。カンだけで(センスだけでも)責任者はつとまりません。昇給やボーナスの対象にもなりません。わたしは頑張ったぶんの評価は欲しいな。そのために!あなたがグラフの見方を身に付ければ、損は最小に得を最大に出来ます。あなたが持つカンとセンスの大きな助けになります。だからグラフの見方を身に付けよう!
・グラフに書かれているタイトルを見て、なんのグラフか確かめる
・よこ軸とたて軸がなにを表(あらわ)しているかそれぞれ単位を確かめる
・ひとメモリが1とは限らないので確かめる
・グラフは大きく変化した点(座標)に注目する(←超ポイント!!)
確認から始めます。小学校までと違いグラフが二つ以上示(しめ)されることも多いんです。これは仕事で二つ以上のグラフを比較することが多いから。グラフや統計は「比較をすること」で意味を持ちます
写真のグラフを「確認してから」問題を読みましょう。文章よりラクに頭に入ってきますよ
[問題1]
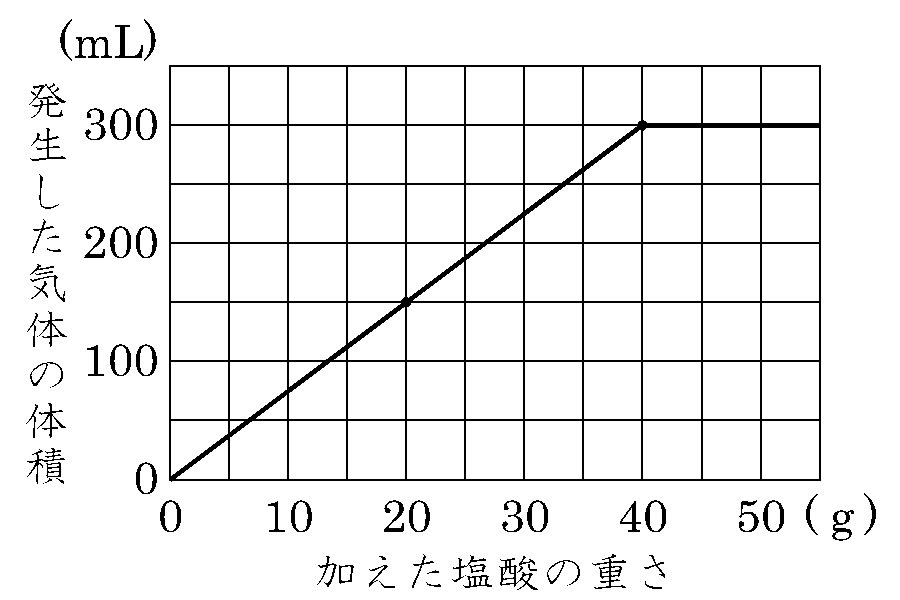
アルミニウム0.2gをいろいろな質量の塩酸にとかしたときに発生する気体の体積を調べたところ、グラフのような結果になりました。これについて、次の問いに答えなさい。
(1) アルミニウム0.2gをすべてとかすには、塩酸が少なくとも何g必要ですか。
(2) アルミニウム1.0gをすべてとかすには、塩酸が少なくとも何g必要ですか。
(3) 750mlの気体を発生させるためには、塩酸が少なくとも何g必要ですか。
(4) 塩酸120gには、最大で何gのアルミニウムをとかすことができますか。
[解説1]
定比例の法則★:化合する物質の質量の比は一定
(よく出る定比例)
銅:酸素=4:1
マグネシウム:酸素=3:2
銅+酸素 → 酸化銅ですから、4+1=5で、銅:酸素:酸化銅=4:1:5になります。同じく、マグネシウム:酸素:酸化マグネシウム=3:2:5になりますね
物質の性質が変わる変化を化学変化★と呼びます。化学変化には化合・酸化や分解・還元があります。化合は物質の性質が変わる化学変化です。性質の変化ですから(気体になって逃げるなどしなければ)全体の質量は変わりません
AとBが化合するときAの質量とBの質量の比は一定です。問題では「よく混ぜた」しか出ませんから、決まった比まで反応仕切った状態です。AとBどちらも決まった比よりたくさんあれば反応せずに残ってしまいます。この反応せず残った物質の量は良く問(と)われます。定比例で反応したぶんを求めて、元の量から引けば残りが出ます
問題に戻ります。もう一度グラフを見ます。このグラフはタイトルありません。よこ軸が「加えた塩酸の重さ(g)」、たて軸が「発生した気体の体積(ml)」。よこ軸は5gずつ、たて軸は50mlずつになっています。大きく変化した点(座標)は (40g,300ml)ですね。ここが過不足なく化合した定比例の状態です
この比を使って問題を解きます。 問題に「アルミニウム0.2gをいろいろな重さの塩酸にとかしたときに発生する気体の体積を調べた」とあります
金属に酸を加えると水素が発生します★
金属の電子(-)が酸のなかの水素イオン(H+)と結びついて水素分子(H2)ができるからです。マイナスとプラスにはくっつくチカラが働きます
金属は熱や電気を流しやすいですよね。金属原子の間を自由に動き回る電子(自由電子)が熱や電流を伝えています。また酸性の物質を酸と呼びます。酸は水に溶かすと水素イオン が発生します。塩酸、硫酸、酢酸(さくさん)、料理酢、レモン水…酸(す)っぱい液体のほとんどは酸です。なお塩酸=塩化水素水溶液で、塩化水素という気体を水に溶かした液体です
問題では、アルミニウム0.2gに塩酸40gが完全に化合し、 水素が300ml発生したことになります
アルミニウム:塩酸:水素=0.2g:40g:300ml
Al:HCl:H2=0.2g:40g:300ml=2:400:3000=1:200:1500
わたしは下の化学式を使って書きます(慣れるとラクです)。比は割合ですから分数と同じく、それぞれに同じ数をかけても割っても変わりません。比で答えるときは割り切れるまで割って簡単な整数比にしておきます
比が出ました。問題は解けます
(1) アルミニウム0.2gをすべてとかすには、塩酸が少なくとも何g必要ですか。
アルミニウム:塩酸:水素=0.2g:40g:300ml
グラフが読めれば計算もいらなかった。(1)はこれだけの問題多いです
(2) アルミニウム1.0gをすべてとかすには、塩酸が少なくとも何g必要ですか。
1.0gは1gと同じではありません。十分の一の位まで確認した測定値★です。実験や観察では誤差が必ず出るので十分の一の位まで確かめるのが決まりです。1gは実際は1.0gかもしれないし1.9gかもしれない。誤差が大きすぎます。測定値1.0も1と同じに計算は出来ますが、測定値を使った計算の答えは十分の一の位まで書かなければいけません
アルミニウム:塩酸:水素=0.2g:40g:300ml=1:200:1500
比がわかってればこれも簡単。単位は付け忘れないで。理科で単位の引っ掛けはよくあります
(3) 750mlの気体を発生させるためには、塩酸が少なくとも何g必要ですか。
アルミニウム:塩酸:水素=0.2g:40g:300ml=1:200:1500
発生した気体ですからここでは水素が750mlということ
300ml× □=750ml → □= 750÷300=5/2(二分の五)
塩酸も同じように× □をすれば答えは出ます
40g × □=40g × 5/2=100g
なお問われてはいませんが、アルミニウムも求められます
0.2g × □=0.2g × 5/2=0.5g
アレ?問題のアルミニウムじゃ足りませんね。だから「少なくとも」って聞いてるのか(イジワルい)。理科は実験・観察ですから、理論通りの結果が出るよう「用意されてる」ことはありません。現象がまずあって、実験や観察と理論を確かめながら役立てていくものです。だから確認の済んだ理論や定理や法則をもとに、実際の実験結果(測定値)を確かめていきます。この確認作業が科学の大部分を占(し)めます。イジワルいのは大問最後の一問くらいですしその正答率は低いので、解けるところだけ確実に解いておけばいいです
(4) 塩酸120gには、最大で何gのアルミニウムをとかすことができますか。
アルミニウム:塩酸:水素=0.2g:40g:300ml=1:200:1500
40g × □=120g
3倍ですね。じゃアルミニウムも
0.2g × □=0.2g × 3=0.6g
あ答え出た。なんだ拍子抜け
ちなみに水素もやっぱり
300ml × □=300ml × 3=900ml
ところで気づいたかな。これ連立方程式と同じなんだよね★
まとめます
・グラフに書かれているタイトルを見て、なんのグラフか確かめる
・よこ軸とたて軸がなにを表(あらわ)しているかそれぞれ単位を確かめる
・ひとメモリが1とは限らないので確かめる
・グラフは大きく変化した点(座標)に注目する(←超ポイント!!)
なお高校数学や物理・化学でわり算はあんまり使いません。分数のかけ算のほうが約分できて早いし割り切れないときは分数で答えるから。ただし 分子/分母が入れ替わってて気付かないミスをしがちなので、元のかけられる数より大きくなるか小さくなるかは確かめてね
(かけられる数)×(分母が大きい分数)=(かけられる数より小)
(かけられる数)×(分母が小さい分数)=(かけられる数より大)
続きます(藤田)
理科は図で理解することの多い教科です
次のオススメはグラフの問題。グラフの見方は社会にも数学にも応用がききます。なにより仕事に直結します。えー服の販売やるのに関係ないよー。ずっと目の前のお客さんだけが相手なら関係ないかもね。あなたが経験を積み店全体で利益を出すとなるとグラフを使わないわけにはいきません。年間を通して一定の利益を上げるにはカンは当たりはずれが大きいから。社長は給料が払えません。カンだけで(センスだけでも)責任者はつとまりません。昇給やボーナスの対象にもなりません。わたしは頑張ったぶんの評価は欲しいな。そのために!あなたがグラフの見方を身に付ければ、損は最小に得を最大に出来ます。あなたが持つカンとセンスの大きな助けになります。だからグラフの見方を身に付けよう!
・グラフに書かれているタイトルを見て、なんのグラフか確かめる
・よこ軸とたて軸がなにを表(あらわ)しているかそれぞれ単位を確かめる
・ひとメモリが1とは限らないので確かめる
・グラフは大きく変化した点(座標)に注目する(←超ポイント!!)
確認から始めます。小学校までと違いグラフが二つ以上示(しめ)されることも多いんです。これは仕事で二つ以上のグラフを比較することが多いから。グラフや統計は「比較をすること」で意味を持ちます
写真のグラフを「確認してから」問題を読みましょう。文章よりラクに頭に入ってきますよ
[問題1]
アルミニウム0.2gをいろいろな質量の塩酸にとかしたときに発生する気体の体積を調べたところ、グラフのような結果になりました。これについて、次の問いに答えなさい。
(1) アルミニウム0.2gをすべてとかすには、塩酸が少なくとも何g必要ですか。
(2) アルミニウム1.0gをすべてとかすには、塩酸が少なくとも何g必要ですか。
(3) 750mlの気体を発生させるためには、塩酸が少なくとも何g必要ですか。
(4) 塩酸120gには、最大で何gのアルミニウムをとかすことができますか。
[解説1]
定比例の法則★:化合する物質の質量の比は一定
(よく出る定比例)
銅:酸素=4:1
マグネシウム:酸素=3:2
銅+酸素 → 酸化銅ですから、4+1=5で、銅:酸素:酸化銅=4:1:5になります。同じく、マグネシウム:酸素:酸化マグネシウム=3:2:5になりますね
物質の性質が変わる変化を化学変化★と呼びます。化学変化には化合・酸化や分解・還元があります。化合は物質の性質が変わる化学変化です。性質の変化ですから(気体になって逃げるなどしなければ)全体の質量は変わりません
AとBが化合するときAの質量とBの質量の比は一定です。問題では「よく混ぜた」しか出ませんから、決まった比まで反応仕切った状態です。AとBどちらも決まった比よりたくさんあれば反応せずに残ってしまいます。この反応せず残った物質の量は良く問(と)われます。定比例で反応したぶんを求めて、元の量から引けば残りが出ます
問題に戻ります。もう一度グラフを見ます。このグラフはタイトルありません。よこ軸が「加えた塩酸の重さ(g)」、たて軸が「発生した気体の体積(ml)」。よこ軸は5gずつ、たて軸は50mlずつになっています。大きく変化した点(座標)は (40g,300ml)ですね。ここが過不足なく化合した定比例の状態です
この比を使って問題を解きます。 問題に「アルミニウム0.2gをいろいろな重さの塩酸にとかしたときに発生する気体の体積を調べた」とあります
金属に酸を加えると水素が発生します★
金属の電子(-)が酸のなかの水素イオン(H+)と結びついて水素分子(H2)ができるからです。マイナスとプラスにはくっつくチカラが働きます
金属は熱や電気を流しやすいですよね。金属原子の間を自由に動き回る電子(自由電子)が熱や電流を伝えています。また酸性の物質を酸と呼びます。酸は水に溶かすと水素イオン が発生します。塩酸、硫酸、酢酸(さくさん)、料理酢、レモン水…酸(す)っぱい液体のほとんどは酸です。なお塩酸=塩化水素水溶液で、塩化水素という気体を水に溶かした液体です
問題では、アルミニウム0.2gに塩酸40gが完全に化合し、 水素が300ml発生したことになります
アルミニウム:塩酸:水素=0.2g:40g:300ml
Al:HCl:H2=0.2g:40g:300ml=2:400:3000=1:200:1500
わたしは下の化学式を使って書きます(慣れるとラクです)。比は割合ですから分数と同じく、それぞれに同じ数をかけても割っても変わりません。比で答えるときは割り切れるまで割って簡単な整数比にしておきます
比が出ました。問題は解けます
(1) アルミニウム0.2gをすべてとかすには、塩酸が少なくとも何g必要ですか。
アルミニウム:塩酸:水素=0.2g:40g:300ml
グラフが読めれば計算もいらなかった。(1)はこれだけの問題多いです
(2) アルミニウム1.0gをすべてとかすには、塩酸が少なくとも何g必要ですか。
1.0gは1gと同じではありません。十分の一の位まで確認した測定値★です。実験や観察では誤差が必ず出るので十分の一の位まで確かめるのが決まりです。1gは実際は1.0gかもしれないし1.9gかもしれない。誤差が大きすぎます。測定値1.0も1と同じに計算は出来ますが、測定値を使った計算の答えは十分の一の位まで書かなければいけません
アルミニウム:塩酸:水素=0.2g:40g:300ml=1:200:1500
比がわかってればこれも簡単。単位は付け忘れないで。理科で単位の引っ掛けはよくあります
(3) 750mlの気体を発生させるためには、塩酸が少なくとも何g必要ですか。
アルミニウム:塩酸:水素=0.2g:40g:300ml=1:200:1500
発生した気体ですからここでは水素が750mlということ
300ml× □=750ml → □= 750÷300=5/2(二分の五)
塩酸も同じように× □をすれば答えは出ます
40g × □=40g × 5/2=100g
なお問われてはいませんが、アルミニウムも求められます
0.2g × □=0.2g × 5/2=0.5g
アレ?問題のアルミニウムじゃ足りませんね。だから「少なくとも」って聞いてるのか(イジワルい)。理科は実験・観察ですから、理論通りの結果が出るよう「用意されてる」ことはありません。現象がまずあって、実験や観察と理論を確かめながら役立てていくものです。だから確認の済んだ理論や定理や法則をもとに、実際の実験結果(測定値)を確かめていきます。この確認作業が科学の大部分を占(し)めます。イジワルいのは大問最後の一問くらいですしその正答率は低いので、解けるところだけ確実に解いておけばいいです
(4) 塩酸120gには、最大で何gのアルミニウムをとかすことができますか。
アルミニウム:塩酸:水素=0.2g:40g:300ml=1:200:1500
40g × □=120g
3倍ですね。じゃアルミニウムも
0.2g × □=0.2g × 3=0.6g
あ答え出た。なんだ拍子抜け
ちなみに水素もやっぱり
300ml × □=300ml × 3=900ml
ところで気づいたかな。これ連立方程式と同じなんだよね★
まとめます
・グラフに書かれているタイトルを見て、なんのグラフか確かめる
・よこ軸とたて軸がなにを表(あらわ)しているかそれぞれ単位を確かめる
・ひとメモリが1とは限らないので確かめる
・グラフは大きく変化した点(座標)に注目する(←超ポイント!!)
なお高校数学や物理・化学でわり算はあんまり使いません。分数のかけ算のほうが約分できて早いし割り切れないときは分数で答えるから。ただし 分子/分母が入れ替わってて気付かないミスをしがちなので、元のかけられる数より大きくなるか小さくなるかは確かめてね
(かけられる数)×(分母が大きい分数)=(かけられる数より小)
(かけられる数)×(分母が小さい分数)=(かけられる数より大)
続きます(藤田)





















