[2024年7月12日 更新]
◆作図問題は難しくなっている
都立高校入試数学では、共通問題でも自校作成問題でも作図問題が出るのが定番。
得点は6点。証明問題(7点)に次いで大きい。
今回はこの作図問題の取り方を解説する。
◆最近は正答率高め
過去の得点率を見てみよう。
2024年度 46.2%
2023年度 54.7%
2022年度 37.0%
2021年度 59.1%
2020年度 66.0%
2019年度 82.2%
2018年度 83.2%
2017年度 67.3%
2016年度 63.2%
2015年度 42.0%
2014年度 40.6%
2014年度、2015年度は正答率は低い。
だが特段に難しい問題とは言えない。2015年度の問題は後述するが、むしろ易しいと言える。
過去問を研究する者がちゃんと点を取っているのだろう。2016~2020年度は6割以上の受験生が点を取っている。
2022年度、ガクンと正答率が下がった。
問題はこれ。

参照:都教育委員会サイト
三角形の面積を二等分する線分を引く。そのための点Pを作図する。実は後述する2015年度の問題とそっくり。
三角形の面積を二等分するなら、底辺の中点を見つければいい。今回は辺ABの垂直二等分線を引くだけ。
「辺ABの垂直二等分線を作図せよ」なら正答率80%を超える。この作業を分かりにくく、中点の性質を理解していなければ正解できないように出題している。
意外と知られていないが、作図問題にも途中点はある。
「点Pを書け」というのに書かなかったりしても点はもらえる。そんなところで減点喰らうようなことをキミたちがするとは思わんがね。
◆覚えるべきはこの3つ
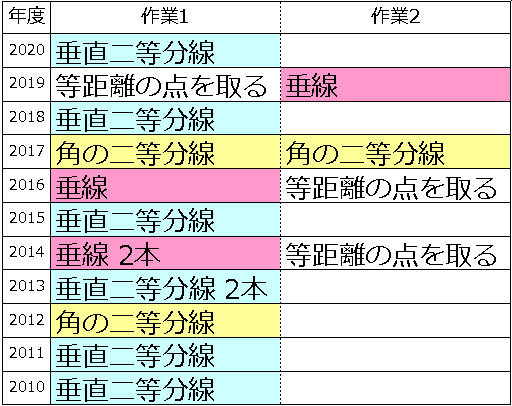
まず都立入試の過去の傾向を見てみよう。
・垂直二等分線
・角の二等分線
・垂線
のうち、いずれかを必ず使うことに気づく。
ここ数年、「1つ作図して終わり」というパターンが減った。複数の作業をしなければならない。
2020年度は垂直二等分線を引いて、点Pと書くだけの簡単な問題。でも正答率は66.0%と高くない。まったく対策をせず、「垂直二等分線で何を表せるか」を理解していないのだろうね。
2021年度は角の二等分線を2本引く問題。
「2辺から等距離にある点の見つけ方」が角の二等分線であることを理解していたら簡単に取れたはず。
10年以上前なら「垂線を作図せよ」「垂直二等分線を作図せよ」という、そのままなやるだけの問題が出されていたのだ。
金輪際、そういう問題は出ないだろう。
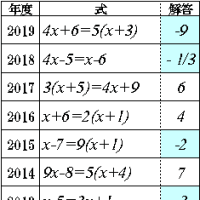
下の問題は2015年度の都立入試共通問題だ。
この問題は1つの作業ができればいい。
ただし
三角形の面積を二等分する → 点Aと、辺BCの中点を通る直線を引けばいい
ということに気づかねばならない。
「辺BCを通る垂直二等分線を引き、辺BCとの交点Dを取る。直線ADを作図せよ」
という問なら、言われたとおりの作業をするだけなのでカンタンだ。
でもそんな問題は出ない。
この2つだけは絶対に覚えておこう。
・角の二等分線・・・2直線から等距離にある点(を結んだ直線)
・垂直二等分線・・・2点から等距離にある点(を結んだ直線)
もう一点。
コンパスは円を描く道具ではない。描けるけど。
コンパスは同じ長さを取ることができる道具である。
なお円とは、中心となる点から等距離にある点を結んだ曲線 である。
覚えておいて損はない。
作図問題は、
何を聞かれているのか。
何を作図すればいいのか。という視点で考えよう。
平均点以上を取りたいのなら、絶対に落とせないのが作図問題だ。
都立入試の過去問や、Vもぎの過去問集で練習できる。
思っている以上に都立入試向けの作図問題がないので困っている。自作のものもあるがまだまだ数が少ない。
希望者が多ければ作って共有したい。
<過去記事:2025年度都立入試に向け、買うべき一冊>
都立に入る! ツイッター 毎日の更新情報を受け取れます












コメントを投稿するにはgooブログのログインが必要です。