前回、スリップ角の話を書きました。まさかの続編です(笑)
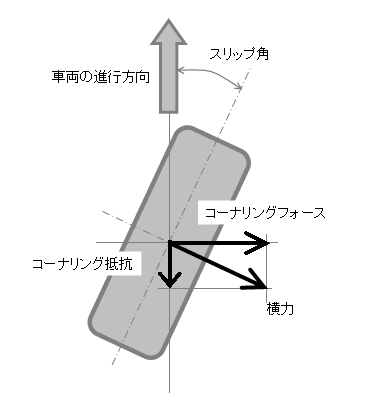
クルマが曲がるにはコーナリングフォース、すなわち車両横方向の力が必要で、その源、横力をタイヤが発生するにはスリップ角という「ずれ」が必要。実はいつものハンドルを切る操作というのは、前輪にスリップ角を与える操作をしている、ということなんだという話でした。
で、今回は横力は発生させるだけじゃなく、曲がることを考えてみたいと思います。
コーナリングの順序
スリップ角やコーナリングフォースのことを考えつつ、コーナリングのしくみを順を追って記述してみたいと思います。
普段何事もないように過ぎていくできごとなのですが、その間にいろんなことが起こっています。
ヨーモーメント
ところで、車両の上下(鉛直)方向を軸とする回転をヨー(yaw)といいます。
同じように左右方向を軸とする回転をピッチ(pitch)、前後方向を軸とする回転をロール(roll)といいますよね。
で、クルマをヨー方向に回転させようとするモーメントをヨーモーメントというわけです。
モーメントは(力×腕の長さ)ですので、この場合、力はコーナリングフォース(右上の図中の Cff,Cfr)、腕の長さは重心からタイヤまでの距離(L1,L2)となります。
右上の図ではFR車をイメージして重心をちょっと前よりに描いてみましたが、例えばMR車やRR車などで重心がリヤよりになる場合、前輪のコーナリングフォースが同じでも発生するヨーモーメントは大きくなり、回頭性に優れることが想像できます。(ただし、コーナリングフォースはタイヤの荷重が大きく関係します。この辺はいわゆる「タイヤの摩擦円」というあたりが関わります。そのうち書く予定…)
自転と公転
また、上の説明で、自転と公転という言葉を使いました。
自転と公転なんていうと惑星運動の話か?って感じなんですが、クルマのコーナリングとは、自転と公転が同時に起こる運動です。たとえばヘアピンカカーブのようなコーナリングを考えたとき、コーナーに沿って移動(=公転)しながら、車自体も180°回転(=自転)していることになります。そんなの当たり前じゃないか!といわれるかもしれませんが、コーナリングには車両の自転(回頭)と公転(旋回)の二つの状態があるというのはポイントだと思います。
例えばぐるぐると定常円旋回を続けている場合、ちょうど月が地球に同じ面を向けるように自転と公転が1:1になっていると言えますが、実際にはコレではどこにも行けません(^^;)ので、直進状態から自転しながらコーナーに進入し、旋回して、さらにこの自転と公転のバランスを崩してまた別の方向に脱出していかなければいけません。こう考えるとコーナリングとは、この自転と公転のバランスを調整することのように思えます。
このバランスを決めるのがクルマの特性であり、また運転です。
極端な話ですが、ドリフト走行などは極端なオーバーステアの状態でバランスしていますよね。これは公転に対して自転が大幅に先行した状態だと言えると思うのです。ドリフト走行ほど極端でなくても、オーバーステアなら自転が先行し、アンダーステアなら公転が先行するというように、実際のクルマの挙動は車両、運転の仕方などによってさまざまに変化します。というわけで、オーバーステアとかアンダーステアとかっていう話題を考えるのにも、この自転と公転っていう考え方はけっこう大事なんではないかな?と考えています。
勉強しながらつづく…予定(笑)
参考文献
三田村楽三:車はなぜ曲がるか?―限界コーナリングのダイナミクス ,山海堂
,山海堂
宇野高明:車両運動性能とシャシーメカニズム ,グランプリ出版 ほか
,グランプリ出版 ほか
クルマが曲がるにはコーナリングフォース、すなわち車両横方向の力が必要で、その源、横力をタイヤが発生するにはスリップ角という「ずれ」が必要。実はいつものハンドルを切る操作というのは、前輪にスリップ角を与える操作をしている、ということなんだという話でした。
で、今回は横力は発生させるだけじゃなく、曲がることを考えてみたいと思います。
コーナリングの順序
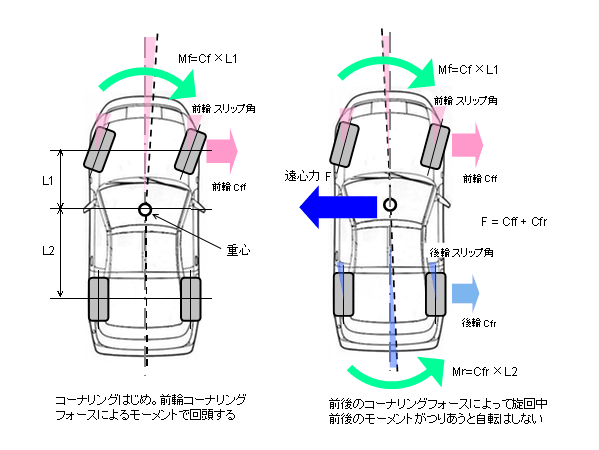 |
| コーナリングフォースとモーメント |
普段何事もないように過ぎていくできごとなのですが、その間にいろんなことが起こっています。
- まず直進状態の車両にドライバーのステアリング操作により前輪にスリップ角が与えられ、前輪はコーナリングフォースを発生する。
- これにより車両にヨーモーメントが付与され車両は回頭(=自転)し向きを変え、徐々に後輪と車両進行方向に角度の差が生まれることで後輪にスリップ角が付く。
- 後輪もコーナリングフォースを発生、後輪によるヨーモーメントが生まれるため、前輪によるヨーモーメントとつりあい状態になり、自転は影をひそめ、旋回(=公転)に移行する。
- 遠心力と向心力がつりあった旋回から、ドライバーはステアリングを徐々に戻すことで前輪スリップ角を減らしていく。これにより前輪は横力を徐々に失い、前輪によるヨーモーメントが減少する。再び自転運動をし、旋回運動から外れていく。
- 車両が向きを変えると後輪スリップ角も減り、コーナリングは終了して脱出する。
ヨーモーメント
ところで、車両の上下(鉛直)方向を軸とする回転をヨー(yaw)といいます。
同じように左右方向を軸とする回転をピッチ(pitch)、前後方向を軸とする回転をロール(roll)といいますよね。
で、クルマをヨー方向に回転させようとするモーメントをヨーモーメントというわけです。
モーメントは(力×腕の長さ)ですので、この場合、力はコーナリングフォース(右上の図中の Cff,Cfr)、腕の長さは重心からタイヤまでの距離(L1,L2)となります。
右上の図ではFR車をイメージして重心をちょっと前よりに描いてみましたが、例えばMR車やRR車などで重心がリヤよりになる場合、前輪のコーナリングフォースが同じでも発生するヨーモーメントは大きくなり、回頭性に優れることが想像できます。(ただし、コーナリングフォースはタイヤの荷重が大きく関係します。この辺はいわゆる「タイヤの摩擦円」というあたりが関わります。そのうち書く予定…)
自転と公転
また、上の説明で、自転と公転という言葉を使いました。
自転と公転なんていうと惑星運動の話か?って感じなんですが、クルマのコーナリングとは、自転と公転が同時に起こる運動です。たとえばヘアピンカカーブのようなコーナリングを考えたとき、コーナーに沿って移動(=公転)しながら、車自体も180°回転(=自転)していることになります。そんなの当たり前じゃないか!といわれるかもしれませんが、コーナリングには車両の自転(回頭)と公転(旋回)の二つの状態があるというのはポイントだと思います。
例えばぐるぐると定常円旋回を続けている場合、ちょうど月が地球に同じ面を向けるように自転と公転が1:1になっていると言えますが、実際にはコレではどこにも行けません(^^;)ので、直進状態から自転しながらコーナーに進入し、旋回して、さらにこの自転と公転のバランスを崩してまた別の方向に脱出していかなければいけません。こう考えるとコーナリングとは、この自転と公転のバランスを調整することのように思えます。
このバランスを決めるのがクルマの特性であり、また運転です。
極端な話ですが、ドリフト走行などは極端なオーバーステアの状態でバランスしていますよね。これは公転に対して自転が大幅に先行した状態だと言えると思うのです。ドリフト走行ほど極端でなくても、オーバーステアなら自転が先行し、アンダーステアなら公転が先行するというように、実際のクルマの挙動は車両、運転の仕方などによってさまざまに変化します。というわけで、オーバーステアとかアンダーステアとかっていう話題を考えるのにも、この自転と公転っていう考え方はけっこう大事なんではないかな?と考えています。
勉強しながらつづく…予定(笑)
参考文献
三田村楽三:車はなぜ曲がるか?―限界コーナリングのダイナミクス
宇野高明:車両運動性能とシャシーメカニズム