ここで当社で考案した方法を紹介します。
1) 周波数を計算したい波形から、5サンプルをとりだします。
1周期がちょうど100サンプルとなる波形を用意しておいて、
任意の位置から5サンプルとりだしてみましょう。
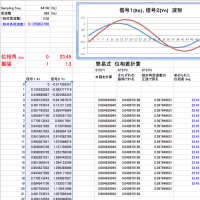
もし、サンプリング周波数が 44100 Hzとすると、この波形の
実周波数は441Hzになります。
時系列波形は;
x[n] = sin ( 2* PI * 441 * (n/44100) ) と計算できますね。
位相差項をいれても構いません。
2) とりだしたサンプルルを、順番に x1, x2, x3, x4 ,x5
とします。
3) 以下のような Ls1 と Ls3を計算します。
Ls1 = x3*x3 - x2*x4
Ls3 = x2*x4 - x1*x5
単純な、一種のたすき掛け演算です。
4) つぎに、Ls1, Ls3 から、 r = Ls3 / Ls1 のように
比をとります。
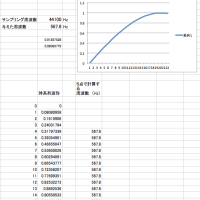
5)以上のように求めた r から次の計算で周波数(瞬時周波数)が
計算できます。
f = (fs / 2 PI) * arcsin ( 0.5 sqrt (3- r) )
fs はサンプリング周波数です。
・ 時系列波形が十分に有効数字のある浮動小数点でしたら
完全に一致します。
・ 正弦波であれば、「どの部分を切り出しても」正しく
求められます。
・ 5サンプルが十分に瞬間とみなせれば周波数の変化も
捉えることができます。
※ 実際の応用では様々な工夫が必要です。
※ 上の例は原理をご理解いただくためのものです。
興味あるかたはお試しください。
最新の画像[もっと見る]













※コメント投稿者のブログIDはブログ作成者のみに通知されます