簡易式 位相差計算方法 (Excel) Vo.2 解説

 

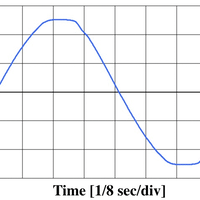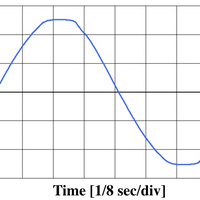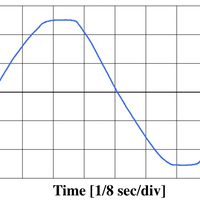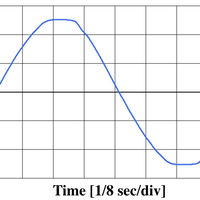
　今回説明する計算は、「２信号の周波数が異なる」ものについてです。信号２の周波数を高めにしてあります。信号１・信号２の間の「位相差」は少しずつ大きくなります。下図のシミュレーションでは位相差の変化がキリのいいような周波数差をわざとつけています。

手順を順番に解説します。

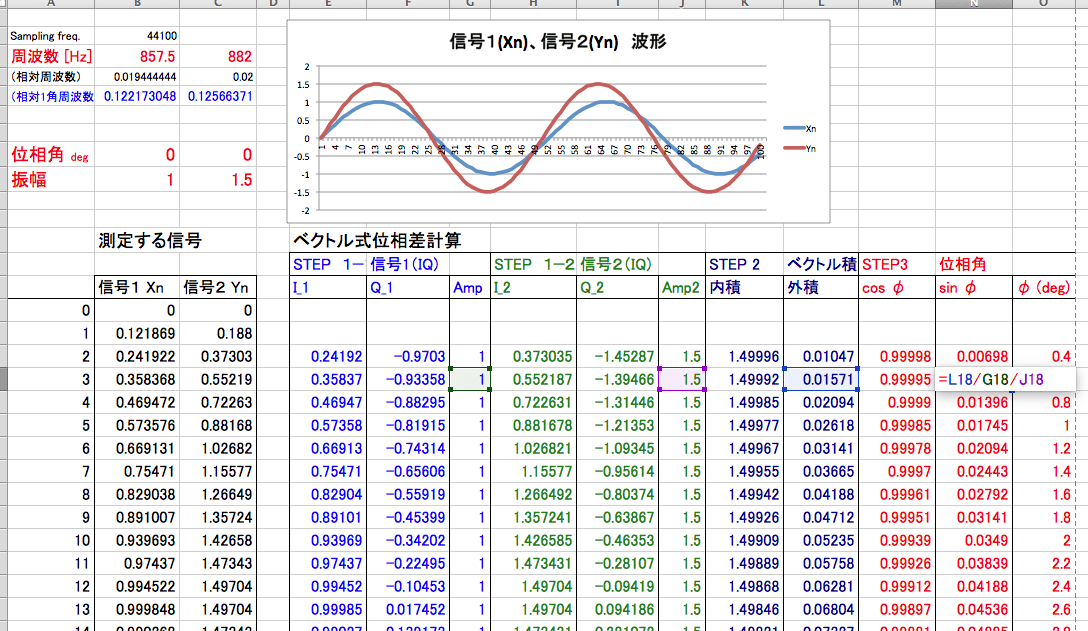
STEP1　２つの信号を「直交化」します。

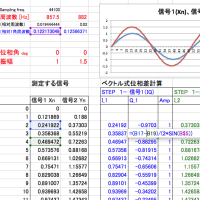
　ヒルベルト変換とか・・・必要？　とか聞かれそうですが。単一成分で、かつ「周波数既知」なら「差分を用いた巧みな方法」があります。Xn から　I,Qをつくるには

I = Xn,  Q = (X[n-1]-X[n+1]) / (2*sinΩ)

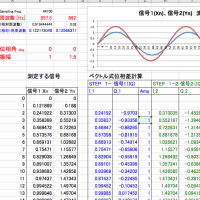
とすることで可能です。Excelでやると下図のようになります。　信号１、信号２　それぞれ同じようにIQ化します。　振幅を確かめると確かに合っています。

相対角周波数 Ω は、 Ω = 2πf/fs のように求めます。(fs:サンプリング周波数）

STEP 2-1　　作成したIQ信号から「内積」をつくります。

s1 =(I_1, Q_1), s2 = (I_2, Q_2)　の複素信号の内積 (Dot)は　

Dot = I_1 * I_2 + Q_1 * Q_2 と計算できます。

STEP 2-2　　作成したIQ信号から「外積」をつくります。

s1 =(I_1, Q_1), s2 = (I_2, Q_2)　の複素信号の外積 (Cross) は　

Cross = I_1 * Q_2 - Q_1 * I_2 と計算できます。

 

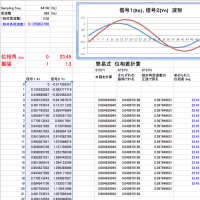
STEP 3 位相差（角）を求めます。

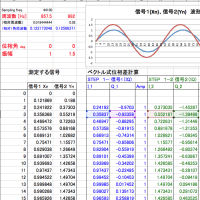
　内積、外積のどちらを使っても位相差 (φ) を求めることができます。下図の例では「外積」をつかったものです。　STEP 2-2 で求めた外積を、　信号１,信号２の振幅の積で割ります。

sin φ = Cross / ( Amp1 * Amp2 )

逆sin を計算して角度が求められます。設定した角度とピタリ一致します。

　

 

---

 

　オシロスコープにリサージュ図を描かせる方法ですと、異なる周波数では、図形が安定しません。「異なる周波数の間で位相差を測って意味あるのか」とお考えのかたもいらしゃるでしょう。しかし周波数がずれているから位相角も変化していると考えるのが自然です。

　逆に、「位相差が変化しないから、周波数は一致している」ともいえます。今まで私たちは位相差をダイレクトに計算する方法を習っておらず、周波数と時間からスタートしていました。位相角を直接測る方法はリサージュ以降、進歩していなかったのかもしれません。

　代替え的には・・・信号がゼロクロスする時刻をみればおおざっぱな位相差はわかるでしょう。しかし、本計算例で示したとおり、信号が数値で与えられているならば、瞬時の位相差はこんなに簡単に計算できるのです。その「位相差の時間変化率」が「周波数差」であり、　2π・Δf = dφ/dt となるのです。

本計算によると、瞬時の位相差が３サンプルで計算できます。

　今回の例を、連続系で考えてみると非常に単純です。直交化するには微分して振幅を補正すればいいだけ。連続系では微分するとωが係数として飛び出しますが、本例の離散系では sinΩとなっているだけの話です。内積・外積を「幾何学的（つまり図形）」にみれば、２つのベクトルのなす角度をcos でみるかsinでみるかの違いだけです。

　角度を360度シームレスに扱うためには、本例のようにcos, sin を同時にあつかえば2πをまたぐ瞬間、arctanを使った場合はπ/2 での符号の反転、など考えなくてすみます。１回転をこえる場合の回転数の検知は簡単です。　内積・外積を実用的に使いこなすには、±90 度で sin を使う計算、 0-180 度の範囲ならcos を使うものが便利です。また感度の良いところは sin =0, cos =0 の周辺ですので、計算条件を工夫することで精密な角度計算ができるのです。

　今回の解説では、２つの信号の「周波数が既知」としましたが、この周波数がわからなければ・・・なにもできません。

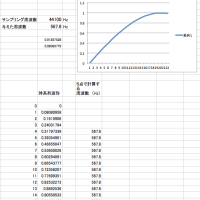
　そんなわけで、Synchro PRIMO法は、なによりも、「瞬時周波数」を計算することを重要視しています。

　「周波数がわかれば／直交化でき／振幅もわかり／ベクトル積を計算すれば角度もわかる」・・・というのが原理なのです。