周波数項が複素数になったら

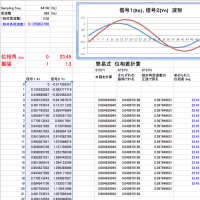
交流波形には、振幅・周波数・初期位相がパラメータとして存在します。

Synchro PRIMO では、リサージュ外積比の平方根の 1/2 を計算し、その値をもとに逆sin を用いて周波数Ω（＝相対角周波）を計算しますが、逆 sin の引数が虚数になった場合、どうするか。

公式ででは、　sin ( j x ) = j * sinh( x ) とされています。

Synchro PRIMO(３倍角法）では、 実は双曲線関数も、計算ができてしまいます。　ただし、3-Ls3/Ls1 < 0  となり開平ができないので、 上の変換を使いarcsin の代わりに asrsinh を使用することになります。 

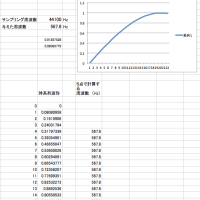
ほかに、Gauss関数、振幅が指数的に増減する信号も、挙動は異なりますが、周波数（一定値）が計算されます。

 

　どの場合でも、周波数＝０に近づけるとその極限値として考えられる波形は、値が一定（電気信号ならDC)　となります。ここを共通点として、パルス、双曲線関数、三角関数、指数関数を・・・「解析接続」して、統一的に扱えないものでしょうか・・・　周波数が存在するなら、基底関数を cos, sin ではなく、cosh, sinh などで構築する「双曲線フーリエ変換」や、ガウス関数を基底とするものが可能なのかもしれません。

 

別のケースとして、 | sin Ω ] > 1 となるケース：  3-Ls3/Ls1  > 4  つまり、 Ls3/Ls1 < -1 で発生します。これも「解析接続」という方法を用いると sin z > 1 のようなケースで、複素数 z を求めることができます。 ちなみに arcsin(2) = は・・・　https://www.wolframalpha.com/input/?i=asin+%282%29&lang=ja  ←こんな答えだそうです。　sinh をベースとする曲線に、振動項が加わるようですが、今の私には解釈不能・・・です。