フーリエ変換使用すると、「成分」を分離することができます。 Synchro PRIMOでは、少ないサンプル数で「単一成分」を精密に計算できますが、「複数成分」の同時計測は可能なのでしょうか。
以前、2成分でシミュレーションを行い理論式も導出してみましたが、意味がさっぱりわかりません。しかし最近になってひとつ重要なことに気づきました。
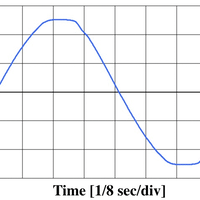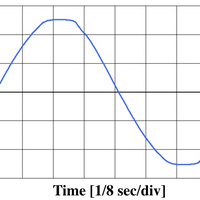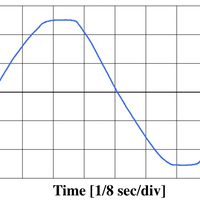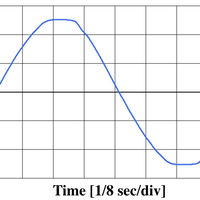
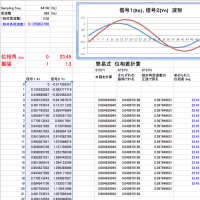
本ブログで紹介しましたが、「2成分の混合波形」は、それぞれの周波数、振幅によって定義される「瞬時周波数」の振る舞いを呈します。この計算式は L.O.コーエンの文献にも解説されていることを紹介しました。 逆に言うと、2成分ということがわかっているなら、瞬時周波数の振る舞いから、それぞれの成分の周波数・振幅を計算できることになります。それぞれの成分の振幅比が大きい場合(=どちらかの成分が優位)瞬時周波数は脈動し、脈動する周期の逆数が「周波数差」として、中心周波数からの変動量で、おそらく・・・振幅が計算できるはずです。
では3成分以上になるとどうか・・・数学的には、未知変数の数+1のデータが要求されます。成分数が無限になると・・・必要なデータ量も増えていきます。実現のためには「時間窓」を大きくし、瞬時性を犠牲にするか、さらに高精度のサンプリングを行うしか方法はありません。
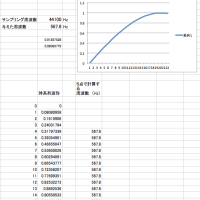
ここで現実的な実装を考えてみます。サンプリング周波数を高くしてみましょう。隣接サンプルとの値の差がどんどんなくなり、振幅方向のさらに高い分解能が必要になります。振幅方向の分解能が高いと、今度はノイズが問題になってきます。
以上をまとめると、成分数(=帯域?)、瞬時性、ノイズの3つの制約が存在し、「超えられない壁」が存在するような予感がします。
実は「時間・周波数・ノイズ」の制約は、なにかシャノンの定理に絡んでいるな・・・と博士課程の段階で気づいていました。シャノンの「通信路容量」は、C = B* log(1+SNR) となります(=シャノン・ハートレーの定理) 。
Synchro PRIMO でもシャノンの定理が見え隠れしているのです。(余談:この関連について博士論文の審査の際、別の先生からコメントがあったらしいです)













※コメント投稿者のブログIDはブログ作成者のみに通知されます