波形データから求める簡易的な位相差計算方法

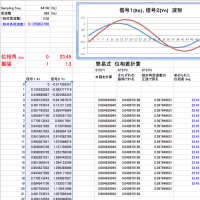
　時系列波形 x[n], y[n]から位相差θを求める
簡易的な「位相差計算方法」を説明します

　サンプリング周波数fs, 周波数ωと振幅Ax,Ay がわかっている
ものとします。

（方法）

1) 周波数を正規化します。 Ω = ω/fs とします. (ω=2πf)

2) 以下のLsを計算します。

　　Ls = x[n] * y[n-1] - x[n-1] * y[n]

3) 位相差 sinθは

sin θ = Ls / (Ax * Ay *sin Ω)

ともとめられます。
　
　上記 Ls は 「波形のどの部分で計算しても」同じ値と
なります。必要あれば、広い区間で平均化して使うといいです。

振幅、周波数が既知である２つの波形の位相差は、上の計算式を
用いて位相差が ±90度の範囲で求めることができます。

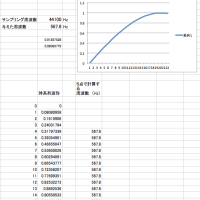
（周期の大きな波形の場合）

１周期のサンプル数が大きい場合、Lsの計算が安定しません。
この場合、2)の処理で、「隣のサンプル」を広くとることができます。

　　Ls = x[n] * y[n-K] - x[n-K] * y[n] のようにLsを計算するなら
　　sin θ = Ls / (Ax * Ay *sin KΩ)

で計算できます。

（証明）

　x[n] = Ax * sin (Ωn)
　y[n] = Ay * sin(Ωn -θ）　

とおいて三角関数の各種公式で展開すると、計算式を導出できます

（問題）

　しかし、ちょっと不満がありますね。
・　振幅と周波数が「既知」でないといけない
・　位相差が ±π/2　の範囲でしか扱えない。

簡易的には利用価値が高いと思いますので、興味あるかたはどうぞ。

もし、周波数は分かっていて、振幅は未知の場合、

波形データから求める簡易的な位相差計算方法 （２）　をお試しください。