５点の値から周波数を求める方法 ・・・ Synchro PRIMO法 ＜Pythonサンプル公開＞

「５点の直から周波数を求める計算式」を以前から紹介しております。

この方法は　Synchro PRIMO法と、筆者は呼んでおります。

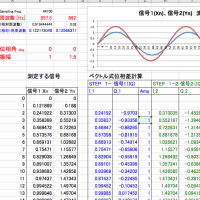
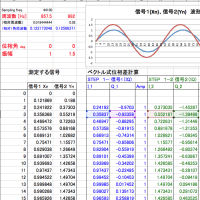
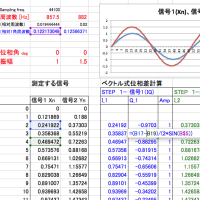
今回、python によるデモを公開します。波形を作成し、Synchro PRIMOで周波数を計算、その結果をグラフ表示するだけのものです。計算プロセスをソースから読み取っていただければ幸いです。

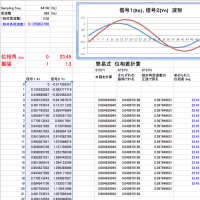
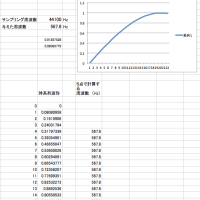
計算結果がグラフに表示されますが、非常に小さな「演算のゆらぎ」が見えますが、これは浮動小数点計算で誤差が蓄積した結果です。サンプルでは、周波数＝ 50.123456789 Hz  と設定していますが、計算結果をみると小数点以下9桁までぎりぎり正しいようです。

６７行目の interval を小さくすると、計算するデータ幅は小さくなりますが、精度は落ちます。

ソース中の、　freq = 50.123456789 　　　# Hz　　を修正し、他の周波数も試してください。周波数が低い時のみ、interval 値は高めにセットし、結果がどうなるか試してみください。

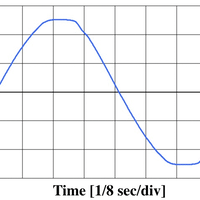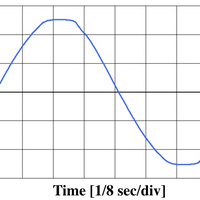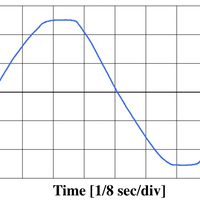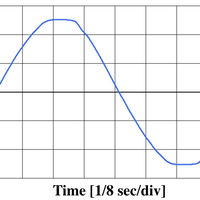
実行すると、波形が表示されます。このウィンドウを閉じると計算を再開し、次に計算結果を表示します。

#========================

import numpy as np

import random

from matplotlib import pyplot as plt

PI2 = np.pi * 2.0

#

# Generate Wave

#

fs = 44100 # sampling freq.

freq = 50.123456789 # Hz

init_phase = 10 # deg.

NumSample = 1000

N = range(0,NumSample)

FREQ = freq / fs

Omega = PI2 * FREQ

Phi = init_phase/ 180.0 * np.pi

# amplitude

Amp_sin = 1.0

# sinusoid

sineWave = np.array( [Amp_sin * np.sin(Omega * n - Phi) for n in N ])

# show wave

waveForm = sineWave

plt.plot(waveForm)

plt.show()

#

# Synchro PRIMO

#

def synchro_primo(x, pos, k=1):

    # samples

    x0 = x[pos - 2*k]

    x1 = x[pos - 1*k]

    x2 = x[pos]

    x3 = x[pos + 1*k]

    x4 = x[pos + 2*k]

 

    # Lissajous Products

    Ls1 = x2 * x2 - x1 * x3

    Ls3 = x1 * x3 - x0 * x4

 

    R = Ls3 / Ls1

 

    sinOmega = 0.5 * np.sqrt( 3 - R )

    Omega = np.arcsin( sinOmega )

    FREQ = Omega / PI2 / k

    freq = FREQ * fs

 

    return  freq

 

#

# calculate Instantaneous frequency

#

Num = 500

Interval = 21     # sampling interval

# output array

calc_freq = []

calc_amp = []

for pos in range(2 * Interval, Num - 4 * Interval):

 

    freq = synchro_primo(waveForm, pos, Interval)

    calc_freq.append(freq)

 

# show Average

print( np.average(calc_freq))

# graph (freq)

plt.plot(calc_freq)

plt.show()