How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)

[Set 1729.03 on Mr. Cube root]

Zoom

[Japanese]

Today's topic is "Feynman vs. The Abacus man"



One afternoon in Rio de Janeiro in 1949, the Nobel Prize winning physicist Richard Feynman accepted a mathematical challenge from a Japanese abacus salesman. Feynman was 31 years old. This story is introduced as "Lucky Numbers" in the Feynman's biography - "Surely You're Joking, Mr Feynman! (Adventures of a Curious Character)".

Feynman is hopelessly beaten by the abacus in addition and subtraction. However he ties at multiplication and is ahead of the abacus man with some long division. Finally the Japanese man shouts out "Raios cubicos!" (which he thinks translates to "Cube roots" in Portugese). Feynman remarks in telling this story, "Cube roots! It's hard to think of a more fundamentally difficult problem in arithmetic. It must have been this guy's most impressive trick on the abacus.”

However, fortune smiles on Feynman because the number chosen to calculate the cube root is 1729.03. Feynman knew that one cubic foot is 1728 cubic inches, and therefore the cube root of 1728 is 12. With this knowledge he was able to calculate 12.002 while the man with the abacus had only got as far as calculating 12-something. This is how Feynman beat the abacus salesman.

Feynman vs. The Abacus
http://www.ee.ryerson.ca/~Elf/abacus/feynman.html

Can someone elucidate for me the arithmetical methodology used by Richard Feynman?
https://www.quora.com/Can-someone-elucidate-for-me-this-arithmetical-methodology-used-by-Richard-Feynman-1

Feynman's calculation (Japanese)
http://www.math.u-ryukyu.ac.jp/~suga/ssh3/node6.html

The number, 1729.03 is close to 1728 (=12^3), it is lucky for Feynman and this is why the anecdote is named as "Lucky Numbers".

I like Feynman and his books, however I felt a disappointment when I read the story.
One reason perhaps because the abacus man is Japanese and the second reason because the abacus man might not have lost if he had kept his composure. Anyway, he felt rushed and could not calculate the correct answer.

How difficult is it to solve cube root of 1729.03 using abacus?
Can we help the abacus man take revenge on Feynman for the first time in 68 years?

I understand what Feynman meant in his book and understand his solution based on Taylor expansion, agree with its effectiveness for the example in this anecdote. This blog article is to show another side of the "Lucky Numbers" story.


Following is the abacus operational steps to solve the cube root of 1729.03. As we cannot find the solution on the Internet, this is probably the first example open to the public.

The abacus operational steps were given by Mr. Ohzeki. He is my friend and the franchiser of the Aoba Keisan Academy (Aoba Calculation Academy - Abacus & Mental calculation school) in Yokohama city. Mr. Ohzeki was the winner of abacus and mental calculation championship several times in Japan. I understood the steps and inserted some detail steps for your better understanding.

In general, you can study abacus operation for Square root and Cube root on the following page.

ADVANCED ABACUS TECHNIQUES JAPANESE SOROBAN & CHINESE SUAN PAN
http://webhome.idirect.com/~totton/soroban/


Abacus steps to solve Cube root of 1729.03

We use the Triple-root method (3-kon method) and approximation method at the end. My special abacus - "Mr. Cube root" is hard to photograph. I use virtual abacus - the [Mr. Cube root] on Excel.


Step 1: Set 1729.03 on F to K.


Step 2: Set the 1st root 1 on B. (1^3=1 which is equal to 1 on F)


Step 3: Subtract 1 (on F) from 1 (1st root).


Step 4: Focus on 729.


Step 5: Divide 729 by 3x1 (1st root). Set answer 24 leaving 9.


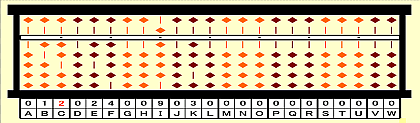
Step 6: Set 2nd root 2 (on C). (2^3=8 is smaller than 24)


Step 7: Subtract 12x2 from 24 (on EF).


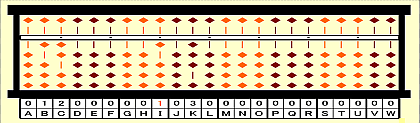
Step 8: Subtract 2nd root 2^3=8 from 9 (on I). Commit 2nd root as 2.


Step 9: Focus on 1030 (on IJKL).


Step 10: Divide 1030 by 3x12.


Step 11: Focus on 28611 (on HIJKL).


Step 12: Divide by 12 which is committed root. Set 5th root 2 on F. (2^3=8 is smaller than 28)


Step 13: Subtract 2x12002 from 28611. Set answer 4607.


Step 14: Focus on 460711 on IJKLMN.


Step 15: Wound up multiplying 460711x36 (3x12).


Step 16: Subtract 5th root 2^3 (=8) and commit 5th root. It means the remainder is 0.165855992 at the root=12.002


Step 17: Divide by 3x12002=36006.


Step 18 Divide by the root 12002. Set the 6th root 3 and subtract 3x120023.


Step 19: Wound up multiplying 100565x36006 (3x12002).


Step 20: Subtract 6th root 3^3 and commit 6th root. Remainder is 0.036209547833. Divide by 3x120023=360069.


Step 21: Estimating error is small at this stage. Continue dividing 1005628000999800 by the given root 120023.


Step 22: Answer is 12.002383786274


Final state: Answer 12.002383786274 (Digits in red mach the real answer.)

We can confirm the answer by iPhone scientific calculator. Correct value is 12.00238378569172 and the result by abacus maches until 8th decimal place. The approximation method is effective to calculate from 5th to 8th decimal place numbers.



Abacus state transition. (Click to Zoom)



We are not sure how much time Feynman took for the calculation. The book says he calculated 5th decimal place (6th root number) - 12.0023 at the end. In the abacus steps, we get the 6th root number at Step 18 and commit it at Step 20.

The abacus man lost by losing mental control and couldn't reach to the 12.002. If he could keep the best condition, I think the calculation battle field might have been 12.00238 or 12.002383. (7 or 8 digits precision)

This is why 1729.03 is the lucky number for Feynman. If the abacus man chose another number, Feynman might have lost the game.


By the way, you can study Square and Cube roots by mental calculation in this page.


About "Raios cubicos!"

In the Feynman's book "Surely You're Joking, Mr Feynman!", the abacus man shouted "Raios cubicos!" when he wants to do cube roots by arithmetic.

Also this story is complicated by the question of how well had Feynman mastered the Portuguese language?

Because Cube Roots in Portugese is "Raizes cubicas" (Pronunciation: haiises kubikas) not "Raios cubicos". The word "Rio (Pronunciation: haio)" (singular form of "Rios") is ray, line, radius, range in English. Volume of a sphere is notated as "4 pi raios cubicos sobre 3" in Portuguese. (sobre="on" in English. Refer to this page.)

So "Raios cubicos!" is somewhat like "Cube radius!" in English. I am not sure the mistake was by Feynman or by abacus man, but we can say "Raios cubicos" is not Cube roots.


29 years have passed since Dr. Feynman's death in 1988. I felt like being with him when I wrote about his calculation match in my blog.

Next article is the beginning of abacus Square root basics.


Movie: Infinity (1996)

You can watch the Feynman v.s. Abacus man scene in the movie "Infinity (1996)". (Movie script, Opening scene.




Related article in English:

Index: Square root and Cube root using Abacus
https://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b


Related articles in Japanese:

Bushi no Kakeibo (Soroban Bushi story in Edo period) - book and movie
https://blog.goo.ne.jp/ktonegaw/e/38e15f47cba2eaed5f1787c30b09eb7c

Slide Rules nostalgia (Concise Slide Rules, Hemmi Slide Rules)
https://blog.goo.ne.jp/ktonegaw/e/b91ae7814c1830a9aaf7da77aadf88a8

Slide rule in Apollo rocket (Pickett N600-ES）
https://blog.goo.ne.jp/ktonegaw/e/3898318d7f4b3e84900d9ae2cb80d816

Mechanical Calculator (Tiger Calculator)
https://blog.goo.ne.jp/ktonegaw/e/226dd92e17d66ac624b7279776aa77f6

Logarithm and Trigonometric function table book 110 years ago.
https://blog.goo.ne.jp/ktonegaw/e/8d90de27b13365139c25bbffd9c4f04b


Please place your mouse on the buttons and click one by one. These are blog ranking sites.