1,000円電卓で解く算数問題

...と、タイトルはありますが「HP50gで解く算数問題3」の続きで、いわゆる御三家の問題を算数で挑戦してみます。

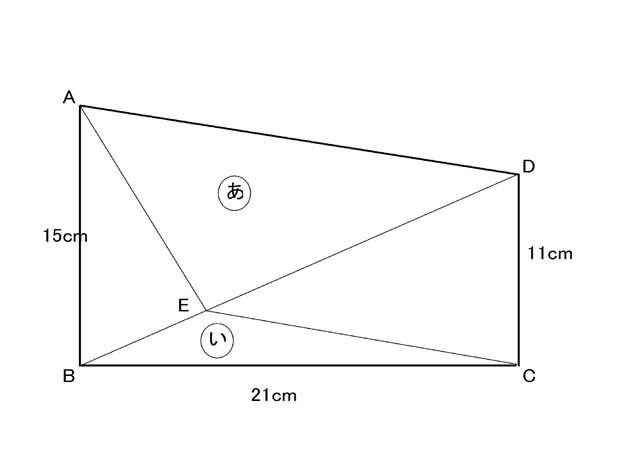
問題：台形ABCDの対角線BD上に、点Eを、ADとECが平行になるようにとりました。
三角形「あ」と三角形「い」の面積を求めなさい。
（2012年　女子学院中）


前の算数問題1と2は、最小自乗法や連立方程式まで使わなくとも算数で解けましたが、、
今回の図形問題は「ひらめき」が必要だと感じます。「い」が難しい。

①ADとECが平行であることから、「あ」と△ACDの面積は同じになるので、11×21÷2で求められる。
②「い」の面積はBDとBEの長さの比率を△ABDと△ABEの面積の比率から求め
③BDとBEの長さの比率が△BCDと「い」の面積の比率が同じになることから求める。

では、SHARPの事務電卓で解いてみます。
CASIOでは÷=を÷÷==と打鍵。[R・CM]は[MR]に読み替えてください。
<...>は電卓の表示画面です。

①11×21÷2［M+]　　　　　　<115.5> ...「あ」の面積
②15×21÷2÷[R・CM]=÷=　　<0.733333333> ...△ABDの面積の中で「あ」の割合
③-1=[+/-]　　　　　　　　　<0.266666667> ...BDの中でBEの割合
×21×11÷2=　　　　　　　　<30.80000003> ...「い」の面積

もう一つ
CEを延長してABと交差する点をFとし、△BCFの11/15とする方法もあります。
21×4÷2×11÷15=　　　<30.8>

算数って面白いなと思いました。

HP50gで解く算数問題3

問題：台形ABCDの対角線BD上に、点Eを、ADとECが平行になるようにとりました。
三角形「あ」と三角形「い」の面積を求めなさい。
（2012年　女子学院中）



小学校6年生までの知識で解ける問題だが、けっこう難しい。
今回もそのまま解いては面白くないので、複素数を使ってみる。

RPNモードで（□は[SPC]　...「　」は説明文）

0□15i×＋'A[STO] ...「( 0,15)を A に保存」
0□0i×＋'B[STO] ...「( 0, 0)を B に保存」
21□0i×＋'C[STO] ...「(21, 0)を C に保存」
21□11i×＋'D[STO] ...「(21,11)を D に保存」

Eの座標は　DROITE関数　で調べる。


DROITE関数は2つの複素数を引数として直線の方程式を返すため
B□D[CAT][DROITE]　とすると　直線BDのグラフと計算式が現れるので面白い。


HP50gは、その気になれば[STO]で数式も保存しておける。
'BD[STO]

次に
C□(0,4)[CAT][DROITE]　で直線CEの方程式
Y=-.190476190476(x-21)　が表示され、これも保存
'CE[STO]

マトリックスライターを起動しBDとCEの式を入力。
そのままBDと打てば先ほどの式が入力される。

再度マトリックスライターを起動し解きたい変数を入力
'X　'Y
[S.SLB]から[LINSO]でEの値［X=5.6 y=2.93333333333］が表示される。
これを E に保存。
X□Yi×＋'E[STO]


＊面積の計算
ようやくお膳立てができたので面積を計算する。
面積の計算にはCMPLX（右シフト1）のF3にある[CONJ]関数をつかう。

A□D[CONJ]×
D□E[CONJ]×＋
E□A[CONJ]×＋
2/



虚数部の115.5が三角形「あ」の面積である。

同様に三角形「い」の面積をCONJ関数で求めると30.8になる。