楽をしよう 計算工夫 われわれ大和民族がんばろう

本日は、計算の工夫について
お話しいたします。

「計算」は、算数にとっては欠かすことのできないツールでもあります。
当たり前ですが。

どんな問題も、答えを出すための途中の考え方が大事ですが、
最終的に答えを出すのは、計算です。

「１００」という答えなのに、「１０１」と答えたら
もうそこでアウトなのです。

ただ、計算というのは、
小学校５年生までに小数、分数の扱い方を習ってしまえば
後は、とにかく自分で使っていくしかないので、
独自のやり方に頼っている部分が大きいかと思います。

また、どの塾でも、
「計算」という授業をカリキュラムに取り入れているところは
ほとんどないのです。
唯一、日能研では、５年生の２月から「小数」「分数」について
ひたすら８回ほど授業が組まれておりますが。

・分数の足し算、引き算では、
仮分数に直して計算するのか、帯分数のままで解き進めるのか
・長い式になった時に、
順番を変えて簡単な数字に直してから計算しているのか

など、
細かい部分ですが、誰かが指摘してあげないと
生徒さんは
ずーっと、特に疑問にも思わず自分のやり方で計算しているのでは
ないかと思います。

具体的にみていきましょう。

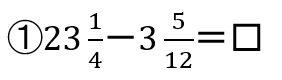
という問題があったとします。
これを、自分のお子様はどうやって解くでしょうか？

これは、あくまでも私の主観ですが、
いきなり仮分数にする生徒さんが圧倒的に多いです。
小学校でそのように先生から言われているのか、
塾の先生が言ったからなのか。

この問題は、
まずは、通分しましょう。

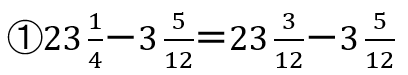
←まだ分数の分子が３−５という状態なのでそのままでは引けません

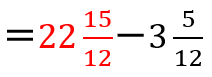
←ここで仮分数にするのではなく、23から1だけを分数にあげて15/12というように、この部分だけ仮分数にします

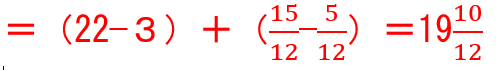
←ここで約分を忘れずに

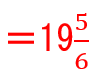
となります。

よく見かけるのは、

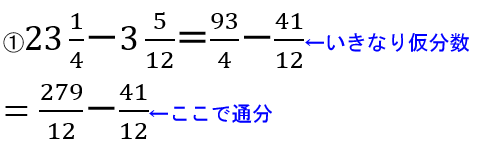
そして、279—41を暗算でできない子は筆算に走ります。
その後、さらに約分も入ってきます。

そもそも、９３を３倍するので大きな数になります。
計算で大事なことは、なるべく小さい数字のままで計算するということです。
計算ミスのリスクを減らすということと
なるべく暗算でできる数字を考えましょう。

次に、長い式の計算ですが、
４つ以上連なっている計算式は何か工夫が隠されていないかということを
まずは考えて欲しいと思います。

②１９＋５４＋７２＋６３＋８１＋３７＋４６＋２８＝□
これも、大多数の生徒さんが、
とにかく左から計算していきます。
もちろん、それでも答えは出せるのですが、

何か工夫はないでしょうか？

「計算で楽する」という発想も大事です。

楽というのは、やはり１００とか１０とかきっかりした数字を作ることです。

１９と組み合わせるのは、一の位に注目して、８１となります。
そうすると、１９＋８１＝１００
同様に、５４＋４６＝１００
７２＋２８＝１００
６３＋３７＝１００

よって、１００が４個できたので、４００
というように、暗算でできます。

それでは、
③９８—６７＋６２＋８７—７８−５２＝□
はどうでしょうか。

これも、左からひたすらやるのではなく、
引いてきっかりする数字を作ってみてください。

答えは、５０です。

このように、計算にもポイントや大事なことが隠されています。
細かい部分ですが、とても大事です。
そういった細かい部分というのは、やはり個別の醍醐味で
隣に生徒さんがいると如実に見えますので
しっかりと指摘してあげることができるのです。

計算は日々の勉強の中に組み込まれている大事な要素です。
算数の細胞と言ってもいいかもしれません。

ウサイン・ボルトとキメットどっちが速いの〜速さの単位換算 大和魂復活

本日は、単位換算についてお話しいたします。

単位換算の問題って、皆さん苦手ですよね？
と、決めつけてはいけませんが、
苦手意識を持っている生徒さんが多いように感じます。

苦手というより、正答にたどり着かない、
わかっているのに一桁間違えてしまうなどなど、
そういったミスが多いのではないでしょうか。

単位換算と言ってもいくつかありますが、
本日は、「速さ」について、お話ししたいと思います。

そもそも、「速さ」ってなんでしょうか？

「Aくんより足が速い」とか「遅い」というのは、
どうやって決まるのと聞くと、

「学校で50m走やった！」とか「僕、クラスで一番だった」とか
「私、今度リレーの選手なんだー」と、
どや顔。

 

で、速いとか遅いってどうやって決まったの？
と再度聞き返すと、
「50m、9.6秒だったけど、A君は、8秒台だった」とか、
「80m走で、7秒台だしたよ」という
具体的な答えが返ってきます。

じゃ、速さって何で決まるんだろう。
50mって距離だよね。
9.6秒って時間だよね。

そう、それだけですね！
考えるのは、「距離」と「時間」だけです。

では、「距離」には、㎝、m、kmという単位があります。
また、「時間」には、秒、分、時間という単位があります。大まかに。

単位変換の時に、問題文に書かれている単位をしっかりと確認して
問題を解き進める必要があります。

ただ、速さの単位変換は、意味を考えれば簡単です！

秒速□m・・・・1秒間にどれだけ進むのか
分速□m・・・・1分でどれだけ進むのか
時速□km・・・・1時間でどれだけ進むのか

その距離を出せばいいのです。

例えば、突然ですが、
ウサイン・ボルトってご存知ですよね。

100mを9.58秒（世界新記録）で走ります。
ということは、100÷9.58＝10.43m/秒
つまり、1秒間に10m強進んでいるということになります。
すごいですよね！！

1秒で10mも先に行ってしまうとは！

で、男子マラソンで世界記録のキメットは、
42.195kmを2時間2分57秒で走ります。

これって、どのくらいすごいことなのでしょうか。

秒速でボルトと比べたいと思います。

長さの単位を変換します。
42.195km＝42195m　(kmからmに変換)

次に時間の単位を変換します。
2時間2分57秒
2時間=120分
↓
120分+2分＝122分
↓
122分×60＝7320秒
↓
7320秒+57秒＝7377秒
（時間から秒に変換）

つまり、
42195m÷7377秒＝5.72m/秒

うーん、惜しい。
ボルトは10.43mなので、届きません。
しかし、秒速では確かにボルトには敵いませんが、
それにしてもすごい速さで、42kmも走っているのですね。

1秒に5.72m
100m走にすると、100÷5.72＝17.4秒

秒速5.72mは、時速に直すと、×60×60÷1000＝×3.6なので、
20.592km/時

よく、マラソン中継で選手の横を自転車で走っている人がいますが、
結構、自転車で全速力でも追いつかないような光景を見たことがありますよね。

それくらい速いってことです。
しかもその速さを42kmも続けるスタミナ。
マラソン選手って本当にすごいなと思います。

それでは、本日は、これくらいに致します。