赤池弘次
「
具体的に何が一番統計的かと言うと
言葉で表現するということなのです。
・・・・
つまり、ものを書くにも話すにも、
統計的な努力をしていることになります。
・・・・
既知の式を組み合わせれば科学的な成果が
得られると考えるのは
甚だしい誤解です。
・・・

研究者というのは
知識で頭の中がいっぱいですから
変わったものは見えない。
それを打ち破るにはすごい努力(注)が必要です。
」
注:ひたすらやりぬく
しつこく繰り返す
「
どんなことでも考えれば解けるという経験
をさせないといけません。
」

感想
とんでもないことをやっても
( 100年かかるかもしれないけれど )
解決できる
答えが出せる
という
大安心が
必要だと感じました
Alan Kay
http://www.mew.org/~kazu/doc/smalltalk.html より
オブジェクト指向の考え方は、生物学とソフトウェア工学
という違った考えの接点として生まれたハッピーなアイディアなのです。
http://www.academyhills.com/gijiroku/alan/27.html より
人はハッピーなアイディアの発見を学習によって会得するのです。
たまに、少し常識はずれのアイディアが浮かぶことがある。
これをブルーのアイディアと呼ぶ。
しかし世の中にはそれらのアイディアを抑圧する要素があり、
それらのアイディアのほとんどは
普通か悪いかのどちらかなので、実際にはそのほうがよいだろう。
しかしたまに、自分がいる状況とは全く関係ない
インスピレーションが突然湧くことがあるが、
これがブルーのアイディアである。
........
このように、創造力と学習の関係は大変危ういものである。
これは特に過去100年ほどの間については真実と言える。
その理由として、
この100年間に起こったいろいろな出来事は、
それ以前の数万年と比較して
驚くほど異なっているからである。
それらは古いアイディアの改良ではなく、ほとんどが真の発明であった。
しかし新しいアイディアは斬新で全く異なる視点を持っているので、
これらの発明やアイディアを学ぶことは容易ではない。
米国の多くの学校は、
子供がGoogleで何かを見つけコピーすると、
それで学んでいると思っている。
しかし私は、子供がそれについての作文を書かない限り
学んだことにならないと主張している。
作文は思考を組織化する。単に博物館の展示物を集めるだけではない。

<< 事例 >>
一つ業界の常識を疑って、脱気装置の適正な使用により
超音波利用効率を上昇させると
業界の常識の根拠が不安定であることが感じられるようになります
製造メーカは個別の特殊な事例ばかりです、
ここから本質的な一般論を見つけることは
新しいアイデアが必要です
ブルーのアイディアは音響流のミクロな検討と、
洗浄システムの検討を結びつける方法に発展しました

物の動きを読む(統計数理)
http://ultrasonic-labo.com/?p=1074
超音波の非線形現象利用
http://ultrasonic-labo.com/?p=3807
超音波コンサルティング
http://ultrasonic-labo.com/?p=2187
複数の超音波プローブを利用した
「測定・解析・評価」技術
http://ultrasonic-labo.com/?p=3755
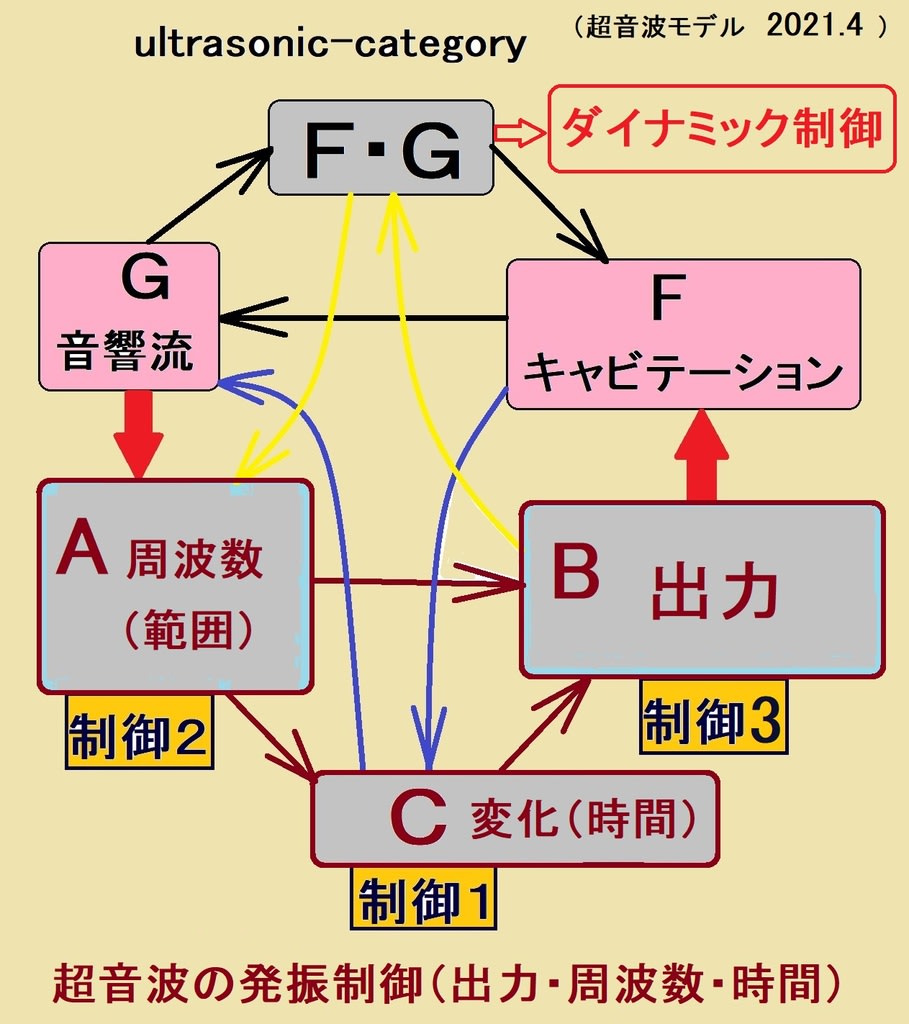
超音波の<ダイナミック特性を利用した制御>
http://ultrasonic-labo.com/?p=3735

超音波<キャビテーション・音響流>技術
http://ultrasonic-labo.com/?p=2950
新しい超音波(測定・解析・制御)技術
http://ultrasonic-labo.com/?p=1454

***********************
超音波システム研究所
ホームページ http://ultrasonic-labo.com/
***********************











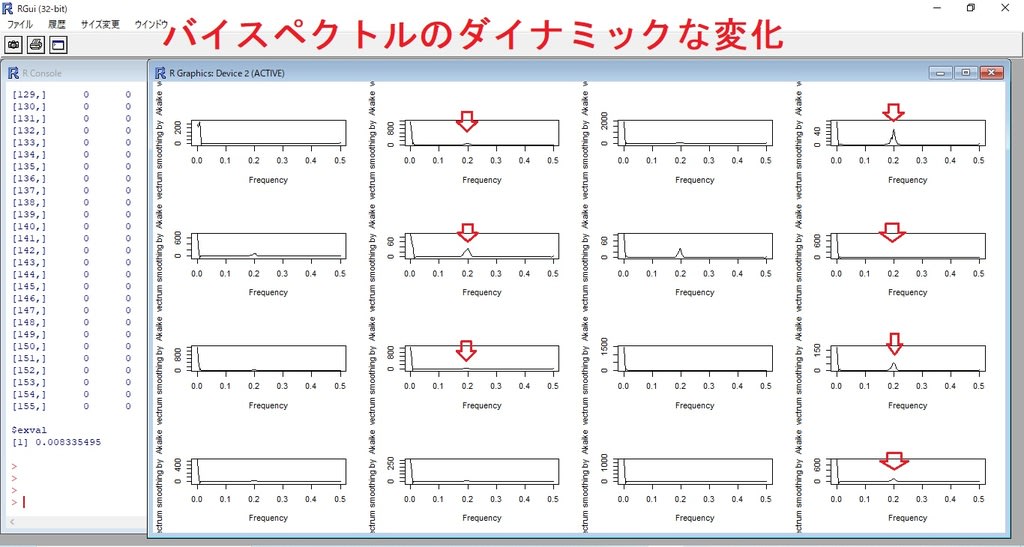

散歩(超音波技術について)
小平邦彦の数学
超音波技術を発展させる
(複雑で難しいものを論理的に考え抜く)ために
1) 数学の重要性を理解する
2) 数学への取り組みを実施する
3) 数学を応用した新しい超音波の利用を進める
と言うことが必要ではないかと考えています
そこで、「数学者(小平邦彦)」の数学に対する
資料・記事を参考のために提示します
小平邦彦『幾何のおもしろさ』
岩波書店(数学入門シリーズ)、1985年
また、十八世紀およびそれ以前においては、
ユークリッド幾何がただ一つの公理的に構成された理論体系であった。
だから私は子供に公理的構成の考えを教える材料は
ユークリッド幾何に限ると思うのである。
近年ユークリッド平面幾何は
数学の初等教育からほとんど追放されてしまったが、
それによって失われたものは
普通に考えられているよりもはるかに大きいのではないかと思う。
昔われわれは平面幾何で論理を学んだんですが、
幾何でないと論理を教えてもだめなんじゃないかしら。
代数なんか材料にして論理を教えようと思っても
材料があんまり単純でしょう。
小平氏は言う。
「わからない証明を繰り返しノートに写してしまうと、
自然にわかってわかってくるようである。
現在の数学の初等・中等教育ではまずわからせることが大切で、
わからない証明を丸暗記させるなどもっての外、
ということになっているが、
果たしてそうか疑問である」
コメント
わからない現象を繰り返し実験確認すると、
自然に問題点が見えてくると感じています
新しいものをつくりだすためには、
第一に、無に耐える力
を身に付けることだと考えます。
「無の哲学」は無に徹し、
何者にも寄りすがらないで
無(考える)ということです。
孤独な思考に耐える精神力が重要です
超音波について
<複数の組み合わせ>
ヒーター、オーバーフロー、立体液循環、液循環ガイド、整流部材、
出力、周波数、複数の台数、制御・・・