波形データから求める簡易的な位相差計算方法 （２）

周波数が既知の波形なら、今回説明する方法で簡単に位相差が計算可能です。

過去の記事　波形データから求める簡易的な位相差計算方法　では、周波数・振幅が既知の場合を紹介しました。今回は周波数のみが既知の場合です。

・　周波数が正確に分かっていれば半周期のデータでも十分です。

・　ノイズの少ない波形で1サイクルが10サンプル程度で表現されている信号であれば、最低３サンプルで計算可能です。（実用上は１サイクル程度の平均化が好ましい）

---

手順を紹介します。

・与える信号を x[n], y[n] とします。サンプリング周波数はfsとします

・x,y には位相差φがあり、周波数はf とします。式で書くと；

　x[k] = Ax sin(2πf/fs・k)

　y[k] = Ay sin(2πf/fs・k -φ)　　　という信号です。

パラメータ A, f, φ が分かっていれば波形 x[n], y[n]は簡単に計算できますが、 その逆の　x[n], y[n]からパラメータA,f, φを求めるのは極めて困難です。

　今回の説明では、 「f　のみが既知」「周波数が同一の２つの信号」を条件に位相差φと振幅 Ax,Ayの求め方を解説します。

---

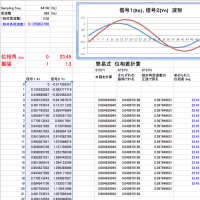
それでは、　x[0],x[1],x[2] .... , y[0],y[1],y[2].....から　 振幅 Ax, Ay, 位相差φを求めてみましょう。

---

STEP1: 　x[n],y[n] をそれぞれ「直交化」します。

　私が考案したトリッキーな方法が便利です。

（１）　まず秘密の定数 A を以下のように計算します。周波数fから下記のようにθを求め、1/cos θの形の係数Aを求めておきます。

  θ = π/2 - (2π * f/fs)  

  A = 1/(2*cos(θ))   のように"定数A"求めます。

（２）　直交信号の作成：Qを合成します。先ほどのAを使います。

x[n] から (I1[n], Q1[n])を、y[n] から (I2[n],Q2[n])を計算します。

　　I1[k] = x[k]

　　Q1[k] = (x[k-1] - x[k+1]) *A

・　信号yも同じように計算し、

　　I2[k] = y[k]

　　Q2[k] = (y[k-1] - y[k+1]) *A

となります。Aは共通です。

x[n]は  X=(I1[n],Q1[n]) 、　y[n]は  Y[n]=(I2[n],Q2[n])のようにベクトルで表現できるようになりました。

---

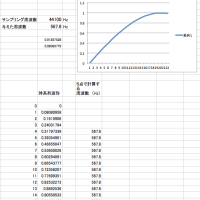
STEP 2: 絶対値の計算

　IQ信号にすると、その絶対値は瞬時振幅となります。自乗和の平方根で振幅が求められます。

  　Ax[k] = √(I1[k]^2 + Q1[k]^2) 

  　Ay[k] = √(I2[k]^2 + Q2[k]^2) 

---

STEP 3: 直交化したX,Yを"ベクトル"とみたて、内積D・外積Cを計算します。　

　　内積: D[k]= I1[k]・I2[k] + Q1[k]・Q2[k]

　　外積: C[k]= I1[k]・Q2[k] - I2[k]・Q1[k]

　位相差が一定の信号であれば, D[k], C[k]は定数になります。実際の計算では多少ばらつくので適当な区間で平均化するといいでしょう。 ノイジーな波形の場合は、平均化して、D, C をもとめておきます。

内積は"ドット積”、外積は"クロス積"とも呼ばれているそうです。

---

STEP4:  位相角を求めるステップです。

　cos , sin を併用する「Phasor形式」で計算してみます。幾何学的に、"２つのベクトルの作る三角形の面積"は、二辺の長さの積 * cos θ = 1/2 *内積×cosθ、または 1/2*外積×sinθで表現できることを利用しています。言われてみれば当たり前なのですが、この対称性が実はポイントです。

　cos φ = D/ (Ax・Ay)

　sin φ = C/ (Ax・Ay)

cos φ, sin φからφを求めるには用途に応じた逆三角関数の計算を行います。

　arcsinを使うと -π/2 ～ +π/2, arccos を使うと 0 ～ ±π　の範囲が使いやすいです。計算が安定しているのは cos φ = 0 の周辺、 sin φ =0 の周辺です。 cos, sin = ±1近傍では 逆三角関数の演算はエラー含みとなります。

---

 

以上でおわりです。

　今回は「周波数のみ既知」としましたが、別の記事で紹介している「瞬時周波数計算」を使用すれば、周波数が未知の信号間の位相差も計算可能です。また、微小に周波数の異なる２つの波形の位相差が刻々と変化する様子も計算できます。　

今回は概要だけを紹介しましたが、後日、さまざまな計算例を説明したいと思います。

---

ご質問・ご要望は  snishie [at] synchro-primo.jp までお寄せください。 説明用のExcel Template 他を用意してあります。

Synchro PRIMO 法のコンセプトは当社ホームページ http://synchro-primo.jp をご覧ください。