微分と差分

　デジタル信号処理では、微分の代わりに差分が用いられ、アナログでは s をつかったラプラス変換、デジタルでは z 変換がいわゆる周波数領域での設計に用いられています。

　z 変換に登場する z^(-1) はデジタル処理では、「一段の遅延」と等価で、この原理が Synchro PRIMO では大きな意味をもっています。

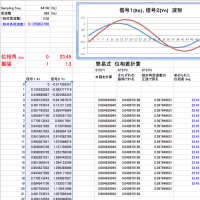
　２階微分を考えてみます。　x(t) = A * sin(ωt)　という連続関数では ω 自乗が飛び出してきて、d2/dt2 x(t) = - (ω^2) sin(ωt) となりますが、「離散系」（＝デジタル）ではどうなるか？

　このあたり、詳しく解説されている専門書・教科書は少ない気がしますが・・・差分演算は連続系の問題を解く際の「近似解法」と考えられているような気配も・・・

計算は難しくありません。一応、「１階差分」をとり、差分の差分として２階差分を計算すると、

Δ(2) x[n] = 1/4 * { x[n+1] + x[n-1] - 2* x[n] } * A

となります。Aは振幅項です。連続系では  - ω^2 となりますが、デジタルではどうなるか。　z 変換 を習ったあとの演習問題としてはよくできていますね。半角の公式が見事にヒットし綺麗にまとまり、

 A = - sin^2(Ω/2) 　　

となります。　

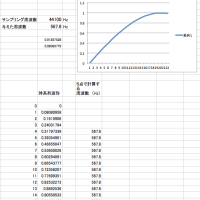
上の式をみたとき・・・積分ではどうなる？　・・・　との疑問から、積分でやってみましたが、「積分」はデジタルでは、どうなるのでしょうか？どう呼べばいいのでしょうか。差分がΔなら、いっそのこと「累積」=Σ と呼んでみることにします。暫定的にやってみると、

Σ(2) x[n] = 1/4 * { x[n+1] + x[n-1] + 2* x[n] } * A

形としては初学の時に習う「平均化」です。 A を計算してみると、今度は、

 A = cos^2(Ω/2)

となります。あれれ？　Δ(2)とΣ(2) を演算子としてみると、振幅項だけでは、　Δ(2) + Σ(2) = 1 ではないですか・・・微分と積分（平均）に着目した演算子では、３項の和差の１箇所しか違わないのに。。。なにかしらの「秘密の恒等式」が隠れている？？？

　これらの演算、振幅項を厳密に求めていることと、一応線形演算なので、私の 「Lissajous 外積」よりははるかにシンプル。積分とはいっても、非常に短い区間での、（一応）「瞬時演算」なのでエンジニアリング向けに何かの用途がありそうです。

　平均化・スムージングといった「実用演算」ではなく、「微分の代用」といった近似演算でもなく、時系列波形をもっと厳密に考えてみたいと思っていました。　下記文献の影響です。もっと理解したいですが、超難解 です ... orz 　

　参考書籍：　

• 飯島泰蔵,  "自然観測法 - 瞬時性に着目した新しい波形解析法,"  森北出版.
• 飯島泰蔵,  "デジタル自然観測法 - 時系列解析のための新しい理論,"  森北出版. 

 PS: 計算式に誤りがあり修正しました。 (2/11)