新石器時代の数学の歴史が見えてきた
1. 神子柴遺跡から見える数学の始まり
神子柴型石斧の生産はどのようなものか

図 100キロメートルを越える移動と集散
神子柴遺跡付近では全国に拡散するほどの多量の石斧を、石材産地で作っていたと思われる
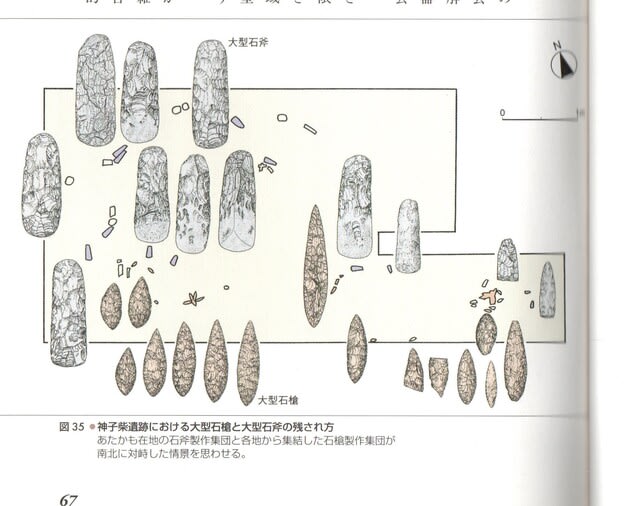
図 神子柴遺跡の石器類

図 尖頭器の集合
神子柴遺跡は石斧、両面加工尖頭器などの各地の石材産地で作られた石器類の集散地では無いか、このような集散地は列島各地にもあったようである。
こうした100キロメートルを越える会合を可能にするためには
月齢のこよみが使われていたのでは無いだろうか
月齢のこよみ無しにそのようなことが可能であるとは思えない、月齢のこよみが存在したのではないかと思う
そうであれば少なくとも月の満ち欠け、月齢を数えるだけの知識があったと考える
それには30と言う数を扱えたと成るのでは無いか
2. 土器の突起とは何か
それは高度な数学認識を示すもので有ると思う

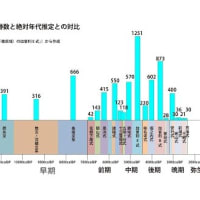
図 突起土器の歴史年表
突起土器を見ると、その初に現れた時を調べると
2、4、6、8、12、3、32、7、5 という数列になる
初現時期の判別は、土器様式からされているものなので、前後関係は変動あるかも知れない
神子柴遺跡の集散と会合から、30までの数学は理解していたものと考えるので
土器の突起で表されていた数字は、単にその数字を表していただけなどとは考えられないのでは無いか
この突起で表されていた数字は、縄文人が別な何らかの知識を示すために
突起土器を作っていたとしか考えられない
ではその核心とは何なのか
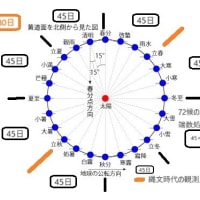
それは月の満ち欠け30に継ぐものとしては太陽の365としか考えられないのでは無いか
30の数学の次の段階としては、一太陽年、365日の数学では無いか
突起土器で示されていたこの数列は、太陽暦を示す暗号では無いのかと考える。
そうだとすればこれまで金生遺跡で見てきたように
金生遺跡の太陽暦と関係するものとして考えることが妥当であると考える
それ以外に何か考えられるだろうか。
数学成立の歴史はこれまでの所、西アジアのメソポタミア文明前後では解明されていない。その歴史解明の中で日本列島の縄文時代などは完全に抜け落ちていた。それでは数学成立の歴史は解明できないはずである。
このように、縄文土器の新石器時代は世界で初めて数学を作りだした時代では無いか
そしてそれは土器で明確に示されていたのでは無いだろうか。
縄文土器の新石器時代は世界で初めて数学を作りだした時代であると考える。

図 文化史年表