本日は、無償学習塾の学習指導に参加しました。高校1年生の生徒さんに、数学Ⅰの「三角比の拡張」を解説しました。
● 三角比をxy座標を用いて考える方法
○ θ=60°の場合
原点Oを中心として半径rの円を描き、角の大きさθが60°となるような点Pを円周上にとります。点Pからx軸に引いた垂線,x軸,線分OP に囲まれた直角三角形に着目します。この直角三角形の∠Oは60°となります。

1つの角の大きさが60°の直角三角形の辺の長さの比は、次の通りです。
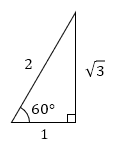
このことから、r=2のとき、Pの座標は (1, √3) となります。

したがって、θ=60°の三角比は次の値となります。
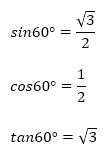
○ θ=120°の場合
原点Oを中心として半径rの円を描き、角の大きさθが120°となるような点Pを円周上にとります。点Pからx軸に引いた垂線,x軸,線分OP に囲まれた直角三角形に着目します。この直角三角形の∠Oは60°となります。

点Pの x, y の正負に注意しつつ(この場合は x<0, y>0 です)、θ=60°の直角三角形を利用して三角比を求めます。先の場合と同様に、r=2のとき、Pの座標は (-1, √3) となります。

したがって、θ=120°の三角比は次の値となります。

三角比を求めるときは、直角三角形の直角とθの角の位置関係に注意する必要があります。本日の生徒さんは、θが90°より大きい場合でも正しく求めることができました。
日本時間15日の午後に、南太平洋のトンガ沖で大規模な海底火山の噴火およびそれに伴う津波が発生しました。日本を含む太平洋沿岸諸国にも津波が到達し、日本国内では大学入学共通テストの日程などにも影響を及ぼしました。トンガや周辺諸国の皆様の無事を願っております。
● 三角比をxy座標を用いて考える方法
- xy座標面において、原点Oを中心とする半径rの円を考えます。r>0です。
- この円周上に点P(x, y)をとり、線分OPを引きます。
- 原点Oを中心に、x軸の正の部分から反時計回り方向を正、時計回り方向を負として、線分OPの回転量を角の大きさθとします。
- 点Pからx軸に引いた垂線,x軸,線分OP に囲まれた直角三角形に着目して、次のように三角比を求めます。(このとき、半径rが直角三角形の斜辺となります。)

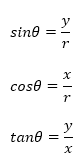
○ θ=60°の場合
原点Oを中心として半径rの円を描き、角の大きさθが60°となるような点Pを円周上にとります。点Pからx軸に引いた垂線,x軸,線分OP に囲まれた直角三角形に着目します。この直角三角形の∠Oは60°となります。

1つの角の大きさが60°の直角三角形の辺の長さの比は、次の通りです。

このことから、r=2のとき、Pの座標は (1, √3) となります。

したがって、θ=60°の三角比は次の値となります。
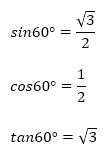
○ θ=120°の場合
原点Oを中心として半径rの円を描き、角の大きさθが120°となるような点Pを円周上にとります。点Pからx軸に引いた垂線,x軸,線分OP に囲まれた直角三角形に着目します。この直角三角形の∠Oは60°となります。

点Pの x, y の正負に注意しつつ(この場合は x<0, y>0 です)、θ=60°の直角三角形を利用して三角比を求めます。先の場合と同様に、r=2のとき、Pの座標は (-1, √3) となります。

したがって、θ=120°の三角比は次の値となります。

三角比を求めるときは、直角三角形の直角とθの角の位置関係に注意する必要があります。本日の生徒さんは、θが90°より大きい場合でも正しく求めることができました。
日本時間15日の午後に、南太平洋のトンガ沖で大規模な海底火山の噴火およびそれに伴う津波が発生しました。日本を含む太平洋沿岸諸国にも津波が到達し、日本国内では大学入学共通テストの日程などにも影響を及ぼしました。トンガや周辺諸国の皆様の無事を願っております。



















