水に小石を投げ込むと、小石が落ちた地点を中心に水が振動します。ギターの弦をはじくと、弦やまわりの空気が振動して音が伝わります。
このように、振動が次々と周囲に伝わる現象を波といいます。水やギターの弦、空気のように、波を伝える性質をもつものを媒質といいます。波が周囲に広がるとき、媒質はその場所で上下または左右に揺れ動くだけで、波とともに移動することはありません。(注意:津波は海水全体が沿岸に押し寄せる現象で、上記の波とは仕組みが大きく異なります。)
波形を図示したときに、その形が正弦曲線(y=Asin(x-p) のグラフの形)となるものを正弦波といいます。波には縦波と横波がありますが、縦波と横波それぞれにおける媒質の挙動を示すプログラムを作成しました。
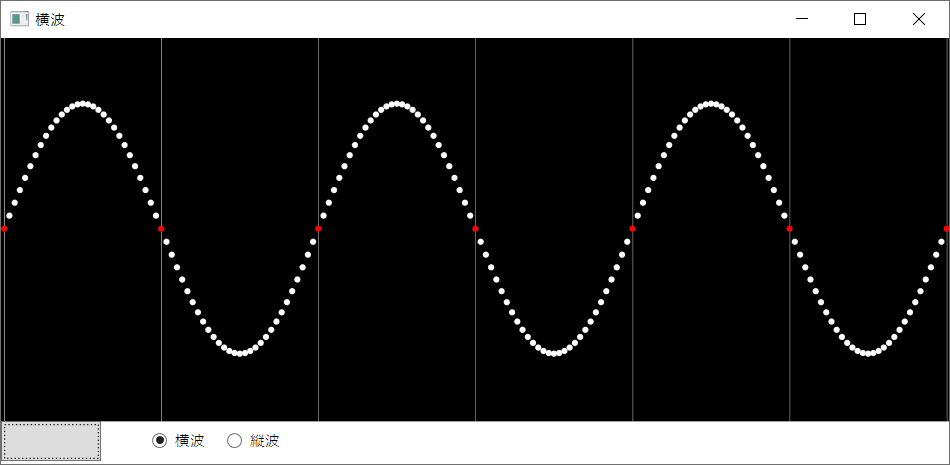
1.横波について
媒質の各点の振動方向と波の進行方向が互いに垂直である波のことを横波といいます。動画の白い点と赤い点が媒質に相当します。このように、媒質はその場で上下に動くだけで、波とともに移動することはありません。
横波の例
● 電磁波(光も含む)
● 地震のS波
など
2.縦波について
媒質の各点の振動方向と波の進行方向が同じである波のことを縦波といいます。疎密波ともいいます。動画の白い点と赤い点が媒質に相当します。このように、媒質はその場で左右に動くだけで、波とともに移動することはありません。
媒質が振動したときの各点の変位量が明瞭になるように、下の図のように縦波を横波表示することが多いです。
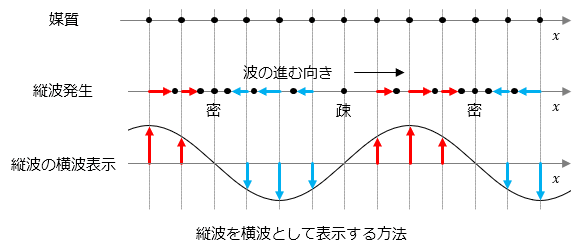
縦波の例
● 音波
● 地震のP波
など
3.その他の重要事項
● 波長
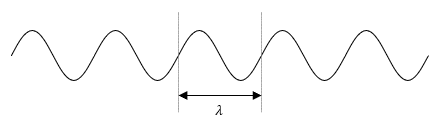
波形は、同じ形の部分 が繰り返されています。この部分の距離を波長といいます。記号は
が繰り返されています。この部分の距離を波長といいます。記号は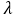 ,単位は m などです。
,単位は m などです。
● 振動数,速さ
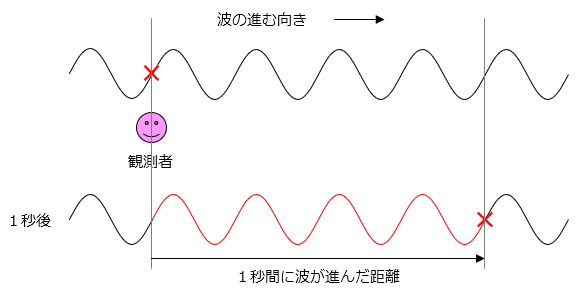
1秒あたりの振動の回数(1秒間に進んだ波に が含まれている個数)を振動数または周波数といいます。記号は
が含まれている個数)を振動数または周波数といいます。記号は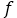 ,単位は 1/s や Hz などです。(この図の波の振動数は4Hzです。)
,単位は 1/s や Hz などです。(この図の波の振動数は4Hzです。)
波長を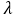 ,振動数を
,振動数を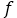 とすると、
とすると、
1秒間に長さ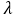 の波長が
の波長が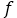 個移動した。⇒ 1秒間に移動した波の距離は
個移動した。⇒ 1秒間に移動した波の距離は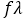 。
。
このことから、波の速さを (単位は m/s など)とすると、
(単位は m/s など)とすると、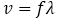 が成り立ちます。
が成り立ちます。
● 周期
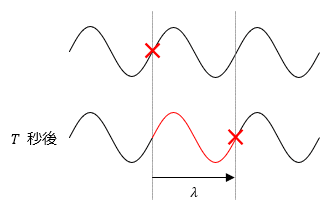
媒質が1回振動するのにかかる時間(1波長 が移動するのにかかる時間)を周期といいます。記号は
が移動するのにかかる時間)を周期といいます。記号は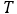 ,単位は 秒 などです。
,単位は 秒 などです。
1秒間に1波長 が
が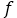 個移動することから、
個移動することから、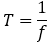 が成り立ちます。
が成り立ちます。
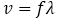 と
と 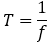 の式を用いると、
の式を用いると、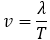 の式が得られます。
の式が得られます。
波は、電車に例えると分かりやすいかもしれません。(各車両の長さはどれも同じである前提とします。)

4.プログラムに関する備考
● Windows WPFプロジェクトで作成し、Window画面内のx軸方向に、等間隔に白い点,赤い点(System.Windows.Shapes.Ellipse)を配置しました。
● 正弦波を表す関数 y=Asin(x-p)(以下、「正弦関数」と表記)を内部的に用意し、時間変化に伴いpの値を大きくすることにより、波の動きを表現しました。
● 横波は、正弦関数を用いて各点のx座標とpの値からy座標の値を求め、対応する位置に点を表示しました。
● 縦波は、縦波を横波表示したときの波形を正弦波とみなし、「(振動中のxの値)=(振動していないときのxの値)+(正弦関数のyの値)」(「縦波の横波表示」の逆の操作)でx座標の値を求め、対応する位置に点を表示しました。
● Window画面と直交座標では座標系が異なるため、Window画面上でも直交座標に見えるように、座標の値を補正して点を表示しました。

このように、振動が次々と周囲に伝わる現象を波といいます。水やギターの弦、空気のように、波を伝える性質をもつものを媒質といいます。波が周囲に広がるとき、媒質はその場所で上下または左右に揺れ動くだけで、波とともに移動することはありません。(注意:津波は海水全体が沿岸に押し寄せる現象で、上記の波とは仕組みが大きく異なります。)
波形を図示したときに、その形が正弦曲線(y=Asin(x-p) のグラフの形)となるものを正弦波といいます。波には縦波と横波がありますが、縦波と横波それぞれにおける媒質の挙動を示すプログラムを作成しました。

1.横波について
媒質の各点の振動方向と波の進行方向が互いに垂直である波のことを横波といいます。動画の白い点と赤い点が媒質に相当します。このように、媒質はその場で上下に動くだけで、波とともに移動することはありません。
横波の例
● 電磁波(光も含む)
● 地震のS波
など
2.縦波について
媒質の各点の振動方向と波の進行方向が同じである波のことを縦波といいます。疎密波ともいいます。動画の白い点と赤い点が媒質に相当します。このように、媒質はその場で左右に動くだけで、波とともに移動することはありません。
媒質が振動したときの各点の変位量が明瞭になるように、下の図のように縦波を横波表示することが多いです。

縦波の例
● 音波
● 地震のP波
など
3.その他の重要事項
● 波長

波形は、同じ形の部分
 が繰り返されています。この部分の距離を波長といいます。記号は
が繰り返されています。この部分の距離を波長といいます。記号は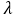 ,単位は m などです。
,単位は m などです。● 振動数,速さ

1秒あたりの振動の回数(1秒間に進んだ波に
 が含まれている個数)を振動数または周波数といいます。記号は
が含まれている個数)を振動数または周波数といいます。記号は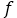 ,単位は 1/s や Hz などです。(この図の波の振動数は4Hzです。)
,単位は 1/s や Hz などです。(この図の波の振動数は4Hzです。)波長を
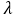 ,振動数を
,振動数を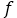 とすると、
とすると、1秒間に長さ
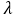 の波長が
の波長が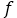 個移動した。⇒ 1秒間に移動した波の距離は
個移動した。⇒ 1秒間に移動した波の距離は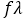 。
。このことから、波の速さを
 (単位は m/s など)とすると、
(単位は m/s など)とすると、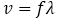 が成り立ちます。
が成り立ちます。● 周期

媒質が1回振動するのにかかる時間(1波長
 が移動するのにかかる時間)を周期といいます。記号は
が移動するのにかかる時間)を周期といいます。記号は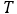 ,単位は 秒 などです。
,単位は 秒 などです。1秒間に1波長
 が
が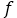 個移動することから、
個移動することから、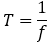 が成り立ちます。
が成り立ちます。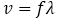 と
と 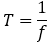 の式を用いると、
の式を用いると、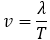 の式が得られます。
の式が得られます。波は、電車に例えると分かりやすいかもしれません。(各車両の長さはどれも同じである前提とします。)

波
電車全体。
波長(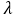 )
)
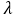 )
)電車1両分の長さ。
振動数(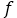 )
)
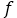 )
)1秒間に電車は何両分進んだのかを示す値。
周期(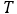 )
)
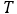 )
)電車1両分が進むのにかかる時間。
速さ( )
)
 )
)電車の速さ。
4.プログラムに関する備考
● Windows WPFプロジェクトで作成し、Window画面内のx軸方向に、等間隔に白い点,赤い点(System.Windows.Shapes.Ellipse)を配置しました。
● 正弦波を表す関数 y=Asin(x-p)(以下、「正弦関数」と表記)を内部的に用意し、時間変化に伴いpの値を大きくすることにより、波の動きを表現しました。
● 横波は、正弦関数を用いて各点のx座標とpの値からy座標の値を求め、対応する位置に点を表示しました。
● 縦波は、縦波を横波表示したときの波形を正弦波とみなし、「(振動中のxの値)=(振動していないときのxの値)+(正弦関数のyの値)」(「縦波の横波表示」の逆の操作)でx座標の値を求め、対応する位置に点を表示しました。
● Window画面と直交座標では座標系が異なるため、Window画面上でも直交座標に見えるように、座標の値を補正して点を表示しました。




















